13、近端策略优化Proximal Policy Optimization (PPO) 算法:从原理到实践
基于LunarLander登陆器的PPO强化学习(含PYTHON工程)
PPO对标的是TRPO算法,改进了其性能。也有学者认为其理论性不强,但实践效果往往不错。
TRPO的缺点:
- 无法处理大参数矩阵:尽管使用了共轭梯度法,TRPO仍然难以处理大的 Fisher矩阵,即使它们不需要求逆
- 近似值可能会违反KL约束,从而导致分析得出的步长过大,超出限制要求
- 我们不能利用一阶随机梯度优化器,例如ADAM
- TRPO 很复杂:TRPO很难解释、实现和调试。当训练没有产生预期的结果时,确定如何提高性能可能会很麻烦。实际也无法保证每一步都能带来改善。
TRPO的改进:近端策略优化算法(PPO)
其他算法:
07、基于LunarLander登陆器的DQN强化学习案例(含PYTHON工程)
08、基于LunarLander登陆器的DDQN强化学习(含PYTHON工程)
09、基于LunarLander登陆器的Dueling DQN强化学习(含PYTHON工程)
10、基于LunarLander登陆器的Dueling DDQN强化学习(含PYTHON工程)
11、基于LunarLander登陆器的A2C强化学习(含PYTHON工程)
TRPO的LunarLander登陆器强化学习(含PYTHON工程):
11.1、信赖域策略优化算法TRPO强化学习-从理论到实践
11.2、信赖域策略优化算法TRPO强化学习-约束优化求解
11.3、信赖域策略优化算法TRPO强化学习-运用实践
参考:Proximal Policy Optimization (PPO) 算法理解:从策略梯度开始
0、近端策略优化PPO核心思路
在传统的策略梯度算法中,我们根据目标函数梯度 ? θ J ( θ ) \nabla_\theta J(\theta) ?θ?J(θ)和步长 α \alpha α更新策略权重,这样的更新过程可能会出现两个常见的问题:
- 过冲(Overshooting):更新错过了奖励峰值并落入了次优策略区域
- 下冲(Undershooting):在梯度方向上采取过小的更新步长会导致收敛缓慢
在监督学习问题中,overshooting并不是什么大问题,因为数据是固定的,我们可以在下一个epoch中重新纠正。
但在强化学习问题中,如果因为overshooting陷入了一个较差的策略区域,则未来的样本批次可能不会提供太多有意义的信息,用较差的数据样本再去更新策略,从而陷入了糟糕的正反馈中无法恢复。较小的学习率可能会解决这个问题,但会导致收敛速度变慢的undershooting问题。
为了避免overshooting带来的严重后果,一种直觉方法是基于KL散度限制每次更新步长的上限:
Δ
θ
?
=
argmax
?
D
K
L
(
π
θ
∥
π
θ
+
Δ
θ
)
≤
?
J
(
θ
+
Δ
θ
)
\Delta\theta^*=\underset{\mathcal{D}_\mathrm{KL}(\pi_\theta\|\pi_{\theta+\Delta\theta})\leq\epsilon}{\operatorname*{argmax}}J(\theta+\Delta\theta)
Δθ?=DKL?(πθ?∥πθ+Δθ?)≤?argmax?J(θ+Δθ)
在TRPO中,结合了自然梯度法的思想,KL散度限制条件被实际运用,具体原理可以参考:TRPO的LunarLander登陆器强化学习(含PYTHON工程):
11.1、信赖域策略优化算法TRPO强化学习-从理论到实践
11.2、信赖域策略优化算法TRPO强化学习-约束优化求解
11.3、信赖域策略优化算法TRPO强化学习-运用实践
如果说,TRPO结合了自然梯度法的思想,并进行KL散度限制。那么PPO实际上是基于普通的A2C与(随机)梯度下降的框架,在此基础上对更新步长进行限制得到的(PPO_v1使用KL散度进行约束,PPO2直接使用clip对步长进行限制)。下面介绍其具体的理论!
目录
1、参数定义
Reward:奖励R,每次(每一步)与环境进行交互都会获得奖励,玩一整局,奖励的和自然是越多越好。
Q(s,a):动作价值函数,其输入为当前状态和要执行的动作,输出为该动作能带来多大的价值,因此,一种贪心的方法是选择能够使Q(s,a)最大动作执行。
Q π ( s t , a t ) = E s t + 1 , a t + 1 , … [ ∑ l = 0 ∞ γ l r ( s t + l ) ] Q_\pi(s_t,a_t)=\mathbb{E}s_{t+1},a_{t+1},\ldots\left[\sum_{l=0}^\infty\gamma^lr(s_{t+l})\right] Qπ?(st?,at?)=Est+1?,at+1?,…[l=0∑∞?γlr(st+l?)]
Q(s,a)的维度等于动作空间的维度。打个简单的比方,假设我现在有两个动作,向北去捡芝麻,向南去捡西瓜。从最终获得的奖励来看,西瓜是大于芝麻的,但是如果芝麻就在我桌上,但是西瓜在20km以外,那可能我还是选择芝麻得了。那么动作价值函数可能就是(1,0.1)。1是捡芝麻的动作价值,0.1是捡西瓜的动作价值,虽说西瓜好吃,但是太远了,所以其动作价值打分特别低。
V(s):状态价值函数,是Q函数的期望。因为期望的积分动作消去了动作A,因此状态价值函数V可以用来直观的反应一个状态的好坏。其实际上是Q(s,a)对不同a的加权平均。
例如,自家高低三路被破,依据这个状态我们就知道现在的状态打分不太行。状态打分不行的原因是每个动作都不会带来太高的打分(都要输了)。
V π ( s t ) = E A t [ Q π ( s t , A t ) ∣ s t ] V_{\pi}(s_{t})=\mathbb{E}_{{A_{t}}}[Q_{\pi}(s_{t},{A_{t}})\mid s_{t}] Vπ?(st?)=EAt??[Qπ?(st?,At?)∣st?]
A:优势函数,其数值等于动作价值函数减去状态价值函数,相当于动作价值Q(s,a)减去了其baseline:
A π ( s , a ) = Q π ( s , a ) ? V π ( s ) A_\pi(s,a)=Q_\pi(s,a)-V_\pi(s) Aπ?(s,a)=Qπ?(s,a)?Vπ?(s)
2、Actor网络构建
2.1 Actor网络基础
Actor网络的核心目的是在一局游戏中获得尽可能多的奖励:
θ
?
=
arg
?
max
?
θ
E
τ
~
p
θ
(
τ
)
[
∑
t
r
(
s
t
,
a
t
)
]
?
J
(
θ
)
\theta^\star=\arg\max_\theta\underbrace{E_{\tau\sim p_\theta(\tau)}\left[\sum_tr(\mathbf{s}_t,\mathbf{a}_t)\right]}_{J(\theta)}
θ?=argθmax?J(θ)
Eτ~pθ?(τ)?[t∑?r(st?,at?)]??
虽然目标函数写成了期望的形式,但是在实际的过程中,我们都是使用蒙特卡洛采样获取其近似的数据:
J
(
θ
)
=
E
τ
~
p
θ
(
τ
)
[
∑
t
r
(
s
t
,
a
t
)
]
≈
1
N
∑
i
∑
t
r
(
s
i
,
t
,
a
i
,
t
)
J(\theta)=E_{\tau\sim p_\theta(\tau)}\left[\sum_tr(\mathbf{s}_t,\mathbf{a}_t)\right]\approx\frac{1}{N}\sum_i\sum_tr(\mathbf{s}_{i,t},\mathbf{a}_{i,t})
J(θ)=Eτ~pθ?(τ)?[t∑?r(st?,at?)]≈N1?i∑?t∑?r(si,t?,ai,t?)
回到理论的表达式,在此要使用梯度下降法,首先要对目标函数求导。简单的直接求导自然是不行的,因为环境中所有数据的获取都依赖与蒙特卡洛采样获取,因此我们需要将其进行变换写为期望的形式:
?
θ
J
(
θ
)
=
∫
?
θ
π
θ
(
τ
)
r
(
τ
)
d
τ
=
∫
π
θ
(
τ
)
?
θ
log
?
π
θ
(
τ
)
r
(
τ
)
d
τ
=
E
τ
~
π
θ
(
τ
)
[
?
θ
log
?
π
θ
(
τ
)
r
(
τ
)
]
\nabla_{\theta}J(\theta)=\int\nabla_{\theta}\pi_{\theta}(\tau)r(\tau)d\tau=\int\pi_{\theta}(\tau)\nabla_{\theta}\log\pi_{\theta}(\tau)r(\tau)d\tau=E_{\tau\sim\pi_{\theta}(\tau)}[\nabla_{\theta}\log\pi_{\theta}(\tau)r(\tau)]
?θ?J(θ)=∫?θ?πθ?(τ)r(τ)dτ=∫πθ?(τ)?θ?logπθ?(τ)r(τ)dτ=Eτ~πθ?(τ)?[?θ?logπθ?(τ)r(τ)]
关注一下其中的
?
θ
log
?
π
θ
\nabla_{\theta}\log\pi_{\theta}
?θ?logπθ?的求解过程,实际过程中这一项会直接包含在softmax层的导数之中。这是为啥呢?看一下交叉熵的公式,策略网络
π
\pi
π的输出实际上就是概率分布,当然
r
(
τ
)
r(\tau)
r(τ)可以作为sample_weight体现在其中。-参考softmax loss详解,softmax与交叉熵的关系:
L
=
?
l
o
g
p
i
,
Y
(
i
)
L=-logp_{i,Y(i)}
L=?logpi,Y(i)?
2.2 重要性采样
为了提升样本的利用率,利用同一批数据进行多次训练,PPO算法中使用了重要性采样的思路。仔细观察原来的目标函数的梯度式子(很多算法在不一定使用奖励
r
(
τ
)
r(\tau)
r(τ),也有使用动作价值函数Q或者动作优势函数A的,但是思路不变):
?
θ
J
(
θ
)
=
E
τ
~
π
θ
(
τ
)
[
?
θ
log
?
π
θ
(
τ
)
r
(
τ
)
]
\nabla_{\theta}J(\theta)=E_{\tau\sim\pi_{\theta}(\tau)}[\nabla_{\theta}\log\pi_{\theta}(\tau)r(\tau)]
?θ?J(θ)=Eτ~πθ?(τ)?[?θ?logπθ?(τ)r(τ)]
假设我们利用策略网络
π
θ
\pi_{\theta}
πθ?与环境进行了交互并得到了一批数据,得到了在策略
π
θ
\pi_{\theta}
πθ?的轨迹
τ
\tau
τ,那么我们运用梯度下降的更新式子就可以得到一个更好的策略
π
θ
′
\pi_{\theta}'
πθ′?:
θ
′
=
θ
?
α
J
′
(
θ
)
\theta'=\theta-\alpha J^{'}\left(\theta\right)
θ′=θ?αJ′(θ)
如果我们需要进行下一次的更新,我们需要用到的策略函数的梯度式子是:
?
θ
′
J
(
θ
′
)
=
E
τ
~
π
θ
′
(
τ
)
[
?
θ
′
log
?
π
θ
′
(
τ
)
r
(
τ
)
]
\nabla_{\theta'}J(\theta')=E_{\tau\sim\pi_{\theta'}(\tau)}[\nabla_{\theta'}\log\pi_{\theta'}(\tau)r(\tau)]
?θ′?J(θ′)=Eτ~πθ′?(τ)?[?θ′?logπθ′?(τ)r(τ)]
其中 π θ ′ \pi_{\theta}' πθ′?我们是已知的,就是期望括号内的内容 ? θ ′ log ? π θ ′ ( τ ) \nabla_{\theta'}\log\pi_{\theta'}(\tau) ?θ′?logπθ′?(τ)我们并不难获得。但是,我们的轨迹数据 τ ~ π θ ′ ( τ ) \tau\sim\pi_{\theta'}(\tau) τ~πθ′?(τ),这就需要我们使用新的策略 π θ ′ \pi_{\theta}' πθ′?重新和环境进行交互才能获得,因此我们原来用来训练的数据训练一次就要丢掉了,很浪费有没有。
重要性采样就是争对这一问题进行改进,该问题的核心是期望的分布
τ
~
π
θ
(
τ
)
\tau\sim\pi_{\theta}(\tau)
τ~πθ?(τ)和梯度项
?
θ
log
?
π
θ
(
τ
)
\nabla_{\theta}\log\pi_{\theta}(\tau)
?θ?logπθ?(τ)依赖于同一个策略网络。重要性采样的基本公式如下所示(可以更换期望服从的分布):
E
x
~
p
(
x
)
[
f
(
x
)
]
=
∫
p
(
x
)
f
(
x
)
d
x
=
∫
q
(
x
)
q
(
x
)
p
(
x
)
f
(
x
)
d
x
=
∫
q
(
x
)
p
(
x
)
q
(
x
)
f
(
x
)
d
x
=
E
x
~
q
(
x
)
[
p
(
x
)
q
(
x
)
f
(
x
)
]
\begin{aligned} E_{x\sim p(x)}[f(x)]& =\int p(x)f(x)dx \\ &=\int\frac{q(x)}{q(x)}p(x)f(x)dx \\ &=\int q(x)\frac{p(x)}{q(x)}f(x)dx \\ &=E_{x\sim q(x)}\left[\frac{p(x)}{q(x)}f(x)\right] \end{aligned}
Ex~p(x)?[f(x)]?=∫p(x)f(x)dx=∫q(x)q(x)?p(x)f(x)dx=∫q(x)q(x)p(x)?f(x)dx=Ex~q(x)?[q(x)p(x)?f(x)]?
由此可得:
?
θ
′
J
(
θ
′
)
=
E
τ
~
π
θ
(
τ
)
[
π
θ
′
(
τ
)
π
θ
(
τ
)
?
θ
′
log
?
π
θ
′
(
τ
)
r
(
τ
)
]
\nabla_{\theta'}J(\theta')=E_{\tau\sim\pi_{\theta}(\tau)}\left[\frac{\pi_{\theta'}(\tau)}{\pi_{\theta}(\tau)}\nabla_{\theta'}\log\pi_{\theta'}(\tau)r(\tau)\right]
?θ′?J(θ′)=Eτ~πθ?(τ)?[πθ?(τ)πθ′?(τ)??θ′?logπθ′?(τ)r(τ)]
小伙伴看到这个式子可以还不太理解,在此解释一下下。
- 假设我们利用策略网络 π θ \pi_{\theta} πθ?与环境进行了交互并得到了一批数据,得到了在策略 π θ \pi_{\theta} πθ?的轨迹 τ \tau τ,那么我们运用梯度下降的更新式子就可以得到一个更好的策略 π θ ′ \pi_{\theta}' πθ′?。此时使用的式子可以是原来的 ? θ J ( θ ) = E τ ~ π θ ( τ ) [ ? θ log ? π θ ( τ ) r ( τ ) ] \nabla_{\theta}J(\theta)=E_{\tau\sim\pi_{\theta}(\tau)}[\nabla_{\theta}\log\pi_{\theta}(\tau)r(\tau)] ?θ?J(θ)=Eτ~πθ?(τ)?[?θ?logπθ?(τ)r(τ)]。
- 使用梯度下降法,我们得到了一个新策略 π θ ′ \pi_{\theta}' πθ′?,如果使用原来的公式 ? θ ′ J ( θ ′ ) = E τ ~ π θ ′ ( τ ) [ ? θ ′ log ? π θ ′ ( τ ) r ( τ ) ] \nabla_{\theta'}J(\theta')=E_{\tau\sim\pi_{\theta'}(\tau)}[\nabla_{\theta'}\log\pi_{\theta'}(\tau)r(\tau)] ?θ′?J(θ′)=Eτ~πθ′?(τ)?[?θ′?logπθ′?(τ)r(τ)],我们会说没有新的策略 π θ ′ \pi_{\theta}' πθ′?重新和环境进行交互的轨迹 τ ~ π θ ′ ( τ ) \tau\sim\pi_{\theta'}(\tau) τ~πθ′?(τ)。此时我们应该使用公式 ? θ ′ J ( θ ′ ) = E τ ~ π θ ( τ ) [ π θ ′ ( τ ) π θ ( τ ) ? θ ′ log ? π θ ′ ( τ ) r ( τ ) ] \nabla_{\theta'}J(\theta')=E_{\tau\sim\pi_{\theta}(\tau)}\left[\frac{\pi_{\theta'}(\tau)}{\pi_{\theta}(\tau)}\nabla_{\theta'}\log\pi_{\theta'}(\tau)r(\tau)\right] ?θ′?J(θ′)=Eτ~πθ?(τ)?[πθ?(τ)πθ′?(τ)??θ′?logπθ′?(τ)r(τ)],不就万事大吉了。
- 使用梯度下降法,我们得到了一个更加新的策略 π θ ′ ’ \pi_{\theta}'’ πθ′?’,继续使用 ? θ ′ ′ J ( θ ′ ′ ) = E τ ~ π θ ( τ ) [ π θ ′ ′ ( τ ) π θ ( τ ) ? θ ′ ′ log ? π θ ′ ′ ( τ ) r ( τ ) ] \nabla_{\theta''}J(\theta'')=E_{\tau\sim\pi_{\theta}(\tau)}\left[\frac{\pi_{\theta''}(\tau)}{\pi_{\theta}(\tau)}\nabla_{\theta''}\log\pi_{\theta''}(\tau)r(\tau)\right] ?θ′′?J(θ′′)=Eτ~πθ?(τ)?[πθ?(τ)πθ′′?(τ)??θ′′?logπθ′′?(τ)r(τ)],就又可以得到 π θ ′ ′ ′ \pi_{\theta}''' πθ′′′?了,这样策略网络 π θ \pi_{\theta} πθ?与环境交互的数据 τ \tau τ就可以被用于训练很多次了。
2.3 PPO Clip
PPO_v1使用KL散度进行约束,PPO2直接使用clip对步长进行限制。此处不介绍PPO_v1了,可以参考Proximal Policy Optimization (PPO) 算法理解:从策略梯度开始。
PPO Clip直接限制策略可以改变的范围。我们重新定义了替代优势:
L
π
θ
C
L
I
P
(
π
θ
k
)
=
E
τ
~
π
θ
[
∑
t
=
0
T
[
min
?
(
ρ
t
(
π
θ
,
π
θ
k
)
A
t
π
θ
k
,
c
l
i
p
(
ρ
t
(
π
θ
,
π
θ
k
)
,
1
?
?
,
1
+
?
)
A
t
π
θ
k
)
]
\begin{gathered}\mathcal{L}_{\pi_\theta}^{CLIP}(\pi_{\theta_k})\\=\mathbb{E}_{\tau\sim\pi_\theta}\left[\sum_{t=0}^T\left[\min\left(\rho_t(\pi_\theta,\pi_{\theta_k})A_t^{\pi_{\theta_k}}\right.,\mathrm{clip}(\rho_t(\pi_\theta,\pi_{\theta_k}),1-\epsilon,1+\epsilon)A_t^{\pi_{\theta_k}}\right)\right]\end{gathered}
Lπθ?CLIP?(πθk??)=Eτ~πθ??[t=0∑T?[min(ρt?(πθ?,πθk??)Atπθk???,clip(ρt?(πθ?,πθk??),1??,1+?)Atπθk???)]?
其中,
ρ
t
\rho_{t}
ρt?为重要性采样:
ρ
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
′
(
a
t
∣
s
t
)
\rho_{t}(\theta)=\frac{\pi_{\theta}(a_{t}\mid s_{t})}{\pi_{\theta'}(a_{t}\mid s_{t})}
ρt?(θ)=πθ′?(at?∣st?)πθ?(at?∣st?)?
clip为截断函数,当重要性采样超出规定的上或下限后,函数会返回对应的上或下限。实际上就是限制两次策略 π θ \pi_{\theta} πθ?和 π θ ′ \pi_{\theta'} πθ′?不能变化太大。
2.4 使用广义优势函数(GAE)代替 r ( s t , a t ) r(\mathbf{s}_t,\mathbf{a}_t) r(st?,at?)
注意观察新的更新式子,其中包含每一步环境给出的奖励
r
(
s
t
,
a
t
)
r(\mathbf{s}_t,\mathbf{a}_t)
r(st?,at?) :
?
θ
′
J
(
θ
′
)
=
E
τ
~
π
θ
(
τ
)
[
π
θ
′
(
τ
)
π
θ
(
τ
)
?
θ
′
log
?
π
θ
′
(
τ
)
r
(
τ
)
]
\nabla_{\theta'}J(\theta')=E_{\tau\sim\pi_{\theta}(\tau)}\left[\frac{\pi_{\theta'}(\tau)}{\pi_{\theta}(\tau)}\nabla_{\theta'}\log\pi_{\theta'}(\tau)r(\tau)\right]
?θ′?J(θ′)=Eτ~πθ?(τ)?[πθ?(τ)πθ′?(τ)??θ′?logπθ′?(τ)r(τ)]
但是在实际过程中,这会给训练带来消极的影响。这点在AC算法的baseline和Dueling DQN中都有提及,其主要原因是奖励
r
(
s
t
,
a
t
)
r(\mathbf{s}_t,\mathbf{a}_t)
r(st?,at?)的均值不一定为0。解决的办法也非常简单,我们可以使用动作优势函数A或者TD error来进行更新。优势函数A已经在1、参数定义中初步介绍了,而A2C算法中TD error的表达式为(具体的推导过程参考【王树森】深度强化学习(DRL)的P16。):
TD?target:
y
t
=
r
t
+
γ
?
ν
(
s
t
+
1
;
w
)
.
TD?error:
δ
t
=
y
t
?
ν
(
s
t
;
w
)
.
\begin{array}{l}{\text{TD target:}}&{y_{t}=r_{t}+\gamma\cdot\nu(s_{t+1};\mathbf{w}).}\\\\{\text{TD error:}}&{\delta_{t}=y_{t}-\nu(s_{t};\mathbf{w}).}\\\end{array}
TD?target:TD?error:?yt?=rt?+γ?ν(st+1?;w).δt?=yt??ν(st?;w).?
当然,还有很多其他形式(GAE 广义优势估计):

而在PPO算法中,我们往往使用广义优势估计Generalized advantage estimation (GAE),GAE方法对这n个k步估计量(k从1到n)进行加权平均,平衡了TD方法和MC方法,同时也平衡了偏差和方差:
A
^
t
G
A
E
(
γ
,
λ
)
:
=
(
1
?
λ
)
(
A
^
t
(
1
)
+
λ
A
^
t
(
2
)
+
λ
2
A
^
t
(
3
)
+
…
)
=
(
1
?
λ
)
(
δ
t
V
+
λ
(
δ
t
V
+
γ
δ
t
+
1
V
)
+
λ
2
(
δ
t
V
+
γ
δ
t
+
1
V
+
γ
2
δ
t
+
2
V
)
+
…
)
=
(
1
?
λ
)
(
δ
t
V
(
1
+
λ
+
λ
2
+
…
)
+
γ
δ
t
+
1
V
(
λ
+
λ
2
+
λ
3
+
…
)
γ
2
δ
t
+
2
V
(
λ
2
+
λ
3
+
λ
4
+
…
)
+
…
)
=
(
1
?
λ
)
(
δ
t
V
(
1
1
?
λ
)
+
γ
δ
t
+
1
V
(
λ
1
?
λ
)
+
γ
2
δ
t
+
2
V
(
λ
2
1
?
λ
)
+
…
)
=
∑
l
=
0
∞
(
γ
λ
)
l
δ
t
+
l
V
\begin{aligned} \hat{A}_{t}^{\mathrm{GAE}(\gamma,\lambda)}& :=(1-\lambda)\left(\hat{A}_{t}^{(1)}+\lambda\hat{A}_{t}^{(2)}+\lambda^{2}\hat{A}_{t}^{(3)}+\ldots\right) \\ &=(1-\lambda)\left(\delta_t^V+\lambda\left(\delta_t^V+\gamma\delta_{t+1}^V\right)+\lambda^2\left(\delta_t^V+\gamma\delta_{t+1}^V+\gamma^2\delta_{t+2}^V\right)+\ldots\right) \\ &=(1-\lambda)\left(\delta_t^V\left(1+\lambda+\lambda^2+\ldots\right)+\gamma\delta_{t+1}^V\left(\lambda+\lambda^2+\lambda^3+\ldots\right)\right. \\ &\left.\gamma^2\delta_{t+2}^V\left(\lambda^2+\lambda^3+\lambda^4+\ldots\right)+\ldots\right) \\ &=(1-\lambda)\left(\delta_{t}^{V}\left(\frac{1}{1-\lambda}\right)+\gamma\delta_{t+1}^{V}\left(\frac{\lambda}{1-\lambda}\right)+\gamma^{2}\delta_{t+2}^{V}\left(\frac{\lambda^{2}}{1-\lambda}\right)+\ldots\right) \\ &=\sum_{l=0}^\infty(\gamma\lambda)^l\delta_{t+l}^V \end{aligned}
A^tGAE(γ,λ)??:=(1?λ)(A^t(1)?+λA^t(2)?+λ2A^t(3)?+…)=(1?λ)(δtV?+λ(δtV?+γδt+1V?)+λ2(δtV?+γδt+1V?+γ2δt+2V?)+…)=(1?λ)(δtV?(1+λ+λ2+…)+γδt+1V?(λ+λ2+λ3+…)γ2δt+2V?(λ2+λ3+λ4+…)+…)=(1?λ)(δtV?(1?λ1?)+γδt+1V?(1?λλ?)+γ2δt+2V?(1?λλ2?)+…)=l=0∑∞?(γλ)lδt+lV??
当 λ = 0 \lambda=0 λ=0时,其会退化为TD Error,可能存在大偏差。当 λ = 1 \lambda=1 λ=1,会考虑全局游戏的优势,可能会有大的方差。
3、Critic网络构建
Critic网络的输入往往是状态矢量,输出为状态价值函数V,其中yt是TD Target。在使用广义优势进行估计的情况下,TD Error被GAE函数替换,因此:
A
^
t
G
A
E
(
γ
,
λ
)
=
y
t
?
ν
(
s
t
;
w
)
\hat{A}_{t}^{\mathrm{GAE}(\gamma,\lambda)}=y_{t}-\nu(s_{t};\mathbf{w})
A^tGAE(γ,λ)?=yt??ν(st?;w)
此时在代码中,TD Target被称为n_step_targets。其计算公式为:
y
t
=
A
^
t
G
A
E
(
γ
,
λ
)
+
ν
(
s
t
;
w
)
{y_t} = \hat A_t^{{\rm{GAE}}(\gamma ,\lambda )} + \nu ({s_t};{\bf{w}})
yt?=A^tGAE(γ,λ)?+ν(st?;w)
Critic训练的实质就是让TD Target接近
ν
(
s
t
;
w
)
\nu ({s_t};{\bf{w}})
ν(st?;w),因此,其使用均方误差函数。

4、关键代码对应
4.1 广义优势函数和n_step_targets计算
A
^
t
G
A
E
(
γ
,
λ
)
=
∑
l
=
0
∞
(
γ
λ
)
l
δ
t
+
l
V
\begin{aligned} \hat{A}_{t}^{\mathrm{GAE}(\gamma,\lambda)}& =\sum_{l=0}^\infty(\gamma\lambda)^l\delta_{t+l}^V \end{aligned}
A^tGAE(γ,λ)??=l=0∑∞?(γλ)lδt+lV??
其中(如果已经done了,那么第二项为0,也就是没有t+1的状态了):
δ
t
=
y
t
?
ν
(
s
t
;
w
)
=
r
t
+
γ
?
ν
(
s
t
+
1
;
w
)
?
ν
(
s
t
;
w
)
\delta_{t}=y_{t}-\nu(s_{t};\mathbf{w})=r_{t}+\gamma\cdot\nu(s_{t+1};\mathbf{w})-\nu(s_{t};\mathbf{w})
δt?=yt??ν(st?;w)=rt?+γ?ν(st+1?;w)?ν(st?;w)
def get_gaes(self, rewards, dones, values, next_values, gamma=0.99, lamda=0.9, normalize=True):
deltas = [r + gamma * (1 - d) * nv - v for r, d, nv, v in zip(rewards, dones, next_values, values)]
deltas = np.stack(deltas)
gaes = copy.deepcopy(deltas)
for t in reversed(range(len(deltas) - 1)):
gaes[t] = gaes[t] + (1 - dones[t]) * gamma * lamda * gaes[t + 1]
target = gaes + values
if normalize:
gaes = (gaes - gaes.mean()) / (gaes.std() + 1e-8)
return np.vstack(gaes), np.vstack(target)
4.2 重要性采样和CLIP
重要性采样公式:
?
θ
′
J
(
θ
′
)
=
E
τ
~
π
θ
(
τ
)
[
π
θ
′
(
τ
)
π
θ
(
τ
)
?
θ
′
log
?
π
θ
′
(
τ
)
r
(
τ
)
]
\nabla_{\theta'}J(\theta')=E_{\tau\sim\pi_{\theta}(\tau)}\left[\frac{\pi_{\theta'}(\tau)}{\pi_{\theta}(\tau)}\nabla_{\theta'}\log\pi_{\theta'}(\tau)r(\tau)\right]
?θ′?J(θ′)=Eτ~πθ?(τ)?[πθ?(τ)πθ′?(τ)??θ′?logπθ′?(τ)r(τ)]
PPO Clip直接限制策略可以改变的范围。我们重新定义了替代优势:
L
π
θ
C
L
I
P
(
π
θ
k
)
=
E
τ
~
π
θ
[
∑
t
=
0
T
[
min
?
(
ρ
t
(
π
θ
,
π
θ
k
)
A
t
π
θ
k
,
c
l
i
p
(
ρ
t
(
π
θ
,
π
θ
k
)
,
1
?
?
,
1
+
?
)
A
t
π
θ
k
)
]
\begin{gathered}\mathcal{L}_{\pi_\theta}^{CLIP}(\pi_{\theta_k})\\=\mathbb{E}_{\tau\sim\pi_\theta}\left[\sum_{t=0}^T\left[\min\left(\rho_t(\pi_\theta,\pi_{\theta_k})A_t^{\pi_{\theta_k}}\right.,\mathrm{clip}(\rho_t(\pi_\theta,\pi_{\theta_k}),1-\epsilon,1+\epsilon)A_t^{\pi_{\theta_k}}\right)\right]\end{gathered}
Lπθ?CLIP?(πθk??)=Eτ~πθ??[t=0∑T?[min(ρt?(πθ?,πθk??)Atπθk???,clip(ρt?(πθ?,πθk??),1??,1+?)Atπθk???)]?
其中,
ρ
t
\rho_{t}
ρt?为重要性采样:
ρ
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
′
(
a
t
∣
s
t
)
\rho_{t}(\theta)=\frac{\pi_{\theta}(a_{t}\mid s_{t})}{\pi_{\theta'}(a_{t}\mid s_{t})}
ρt?(θ)=πθ′?(at?∣st?)πθ?(at?∣st?)?
def ppo_loss(self, y_true, y_pred):
# Defined in https://arxiv.org/abs/1707.06347
advantages, prediction_picks, actions = y_true[:, :1], y_true[:, 1:1 + self.action_space], y_true[:,
1 + self.action_space:]
LOSS_CLIPPING = 0.2
ENTROPY_LOSS = 0.001
prob = actions * y_pred
old_prob = actions * prediction_picks
prob = K.clip(prob, 1e-10, 1.0)
old_prob = K.clip(old_prob, 1e-10, 1.0)
ratio = K.exp(K.log(prob) - K.log(old_prob))
p1 = ratio * advantages
p2 = K.clip(ratio, min_value=1 - LOSS_CLIPPING, max_value=1 + LOSS_CLIPPING) * advantages
actor_loss = -K.mean(K.minimum(p1, p2))
entropy = -(y_pred * K.log(y_pred + 1e-10))
entropy = ENTROPY_LOSS * K.mean(entropy)
total_loss = actor_loss - entropy
return total_loss
4.3 使用同一批数据多次更新
# 得到1000个数据训练10次
# training Actor and Critic networks
a_loss = self.Actor.Actor.fit(states, y_true, epochs=self.epochs, verbose=0, shuffle=self.shuffle)
c_loss = self.Critic.Critic.fit([states, values], target, epochs=self.epochs, verbose=0, shuffle=self.shuffle)
5、基于LunarLander登陆器的PPO强化学习
代码在最上面链接(来自github,修改一下滴,但是原来链接找不到了),跑个200分比较轻松,比TRPO要好一些吧,训练过程如下所示:
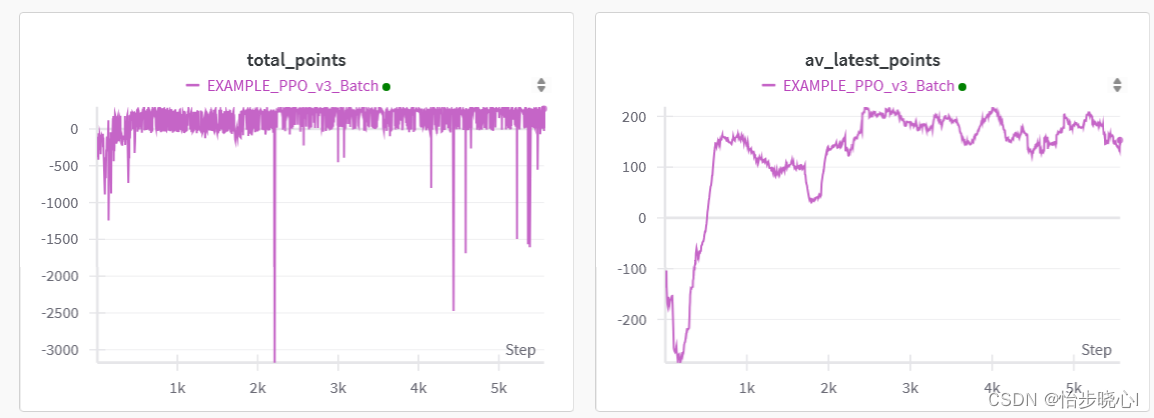
进行测试,效果杠杠的:
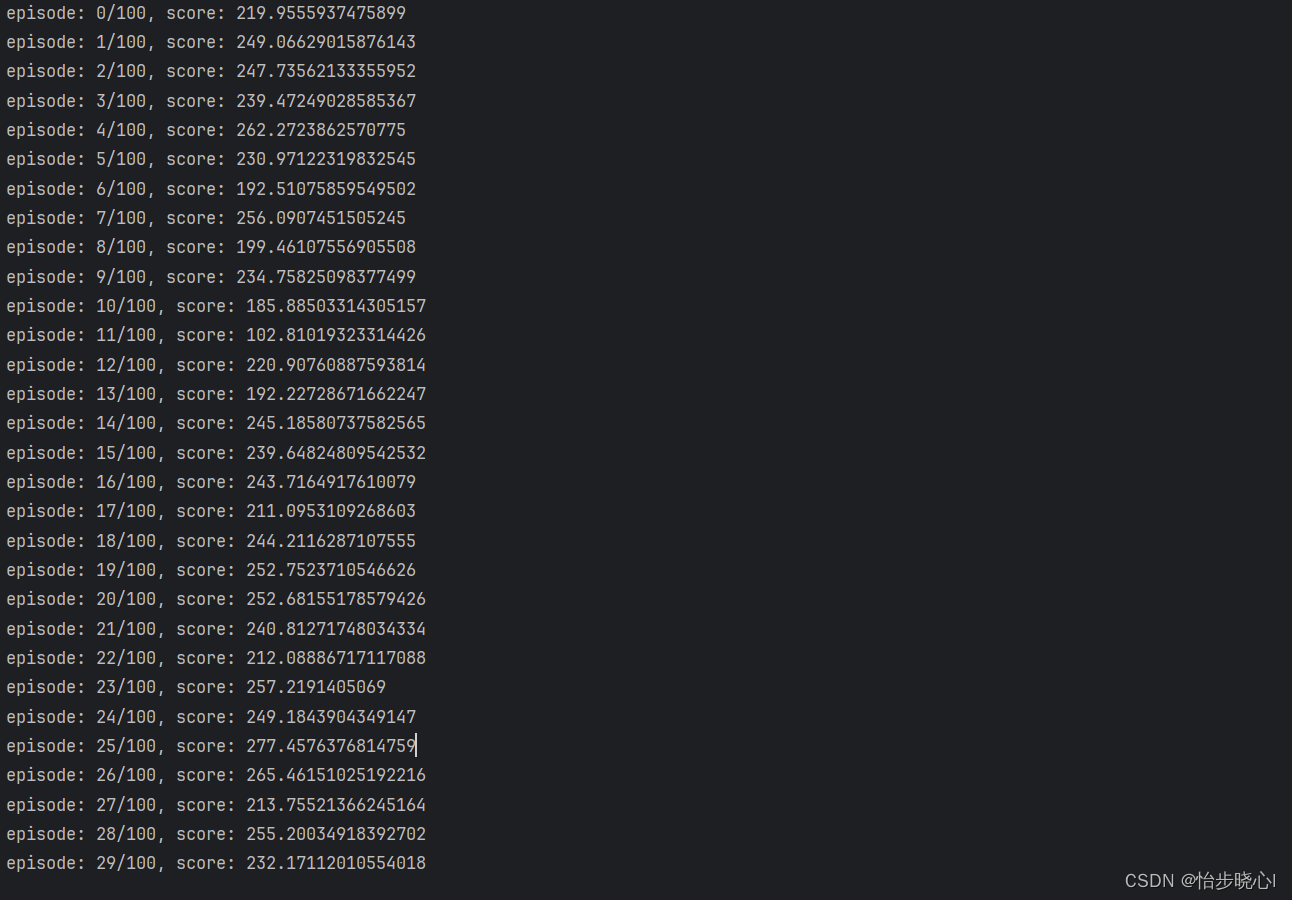
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 2022-ECCV-Explaining Deepfake Detection by Analysing Image Matching
- c++day5(2024/1/2)
- 使用ssh连接远程电脑WSL2最简单的方法,无需设置端口转发!
- 2024年U.S.News全美最佳大学排名公布(附top100榜单)
- JDK8-JDK17版本升级
- zblog主题模板:zblog主题wordprses工业产品企业主题
- 鸿蒙(HarmonyOS)项目方舟框架(ArkUI)控件的部分公共属性和事件
- 问题解决:No module named ‘apex‘,apex安装
- c++动态内存与智能指针
- RPC教程 2.支持并发与异步的客户端