排序嘉年华———选择排序和快排原始版
发布时间:2023年12月20日
一.选择排序
在进行大佬“快排”之前先来一道开胃小菜————选择排序
选择排序是一种简单直观的排序算法,它的基本思想是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
选择排序的具体步骤如下:
1.在未排序序列中找到最小(或最大)的元素,存放到排序序列的起始位置。
2.从剩余未排序元素中继续寻找最小(或最大)的元素,放到已排序序列的末尾。
3.重复步骤2,直到所有元素均排序完毕。

两端同时选择进行排序整理。
void Selectsort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] < a[mini])
{
mini = begin;
}
if (a[i] > a[maxi])
{
maxi = begin;
}
}
Swap(&a[begin], &a[mini]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
每次有两个数被整理到队首和队尾,但由于先更新的是最小值mini所以,如果begin刚好是最大值的话,在进行
Swap(&a[begin], &a[mini]);
时,把最大值下标与最小值下标交换了,因此我们需要加一步判断
if (maxi == begin)
{
maxi = mini;
}

二.霍尔版快速排序

霍尔版快速排序的基本思想是通过一趟排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的数据小,然后再按此方法对这两部分数据分别进行快速排序,递归地进行下去,直到整个序列有序。
霍尔版快速排序的具体步骤如下:
1.选择一个基准元素,通常是序列中的第一个元素。
2.设置两个指针,一个指向序列的起始位置,另一个指向序列的末尾。
3.移动指针,使得左指针指向大于等于基准元素的值,右指针指向小于等于基准元素的值,然后交换两个指针所指向的元素。
4.重复步骤3,直到两个指针相遇。
5.将基准元素与相遇位置的元素交换。
6.递归地对基准元素左右两部分进行快速排序。
1.单趟思想
int left = begin, right = end;
int keyi = begin;
while (left < right)
{
//右边找小
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边找大
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);

由于从右边开始找大,所以结束时左右相遇点一定小于等于key,则最后要将left与keyi交换
2.递归多趟
将keyi更新为相遇点即left/right递归keyi的左边和右边keyi这个位置算已经排好
keyi = left;//更新相遇点为keyi
//递归
Quiksort(a, begin, keyi - 1);
Quiksort(a, keyi + 1, end);
结束条件为左边或右边只有一个数或没有值
//递归条件
if (begin > end)
return;

通过多次递归,左边的每一个值都带上了五角星符号,意味着排序成功
3.寻找中间值作为key
如果在排序有序,或者数据太过极端时,盲目使用left作为keyi,会降低排序效率,这时候就需要在找keyi时进行筛选。
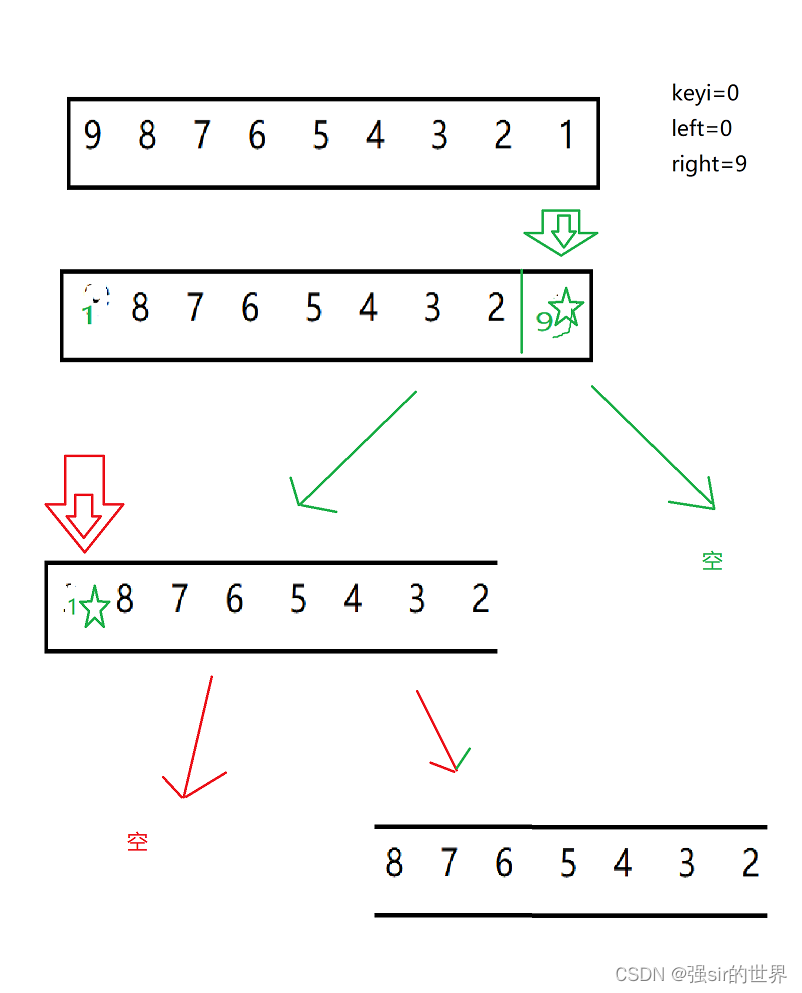
如图这样就无法发挥好快排的双线优势
所以此时我们需要找到中间值进行交换
int GetMidi(int* a, int begin, int end)
{
int midi = (begin + end) / 2;
// begin end midi三个数选中位数
if (a[begin] < a[midi])
{
if (a[midi] < a[end])
return midi;
else if (a[begin] > a[end])
return begin;
else
return end;
}
else//a[begin]>=a[midi]
{
if (a[midi] > a[end])
return midi;
else if (a[begin] < a[end])
return begin;
else return end;
}
}
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
选取10万个数据随机数进行效率检测
void TestOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
{
a1[i] = rand();
a2[i] = rand();
a3[i] = rand();
a4[i] = rand();
a5[i] = rand();
}
int begin1 = clock();
Insertsort(a1, N);
int end1 = clock();
int begin2 = clock();
Bubblesort(a2, N);
int end2 = clock();
int begin3 = clock();
Shellsort(a3, N);
int end3 = clock();
int begin4 = clock();
Quiksort(a4, 0,N-1);
int end4 = clock();
int begin5 = clock();
Heapsort(a5, N);
int end5 = clock();
printf("Insertsort:%d\n", end1 - begin1);
printf("Bubblesort:%d\n", end2 - begin2);
printf("Shellsort:%d\n", end3 - begin3);
printf("Qucksort:%d\n", end4 - begin4);
printf("Heapsort:%d\n", end5 - begin5);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
}
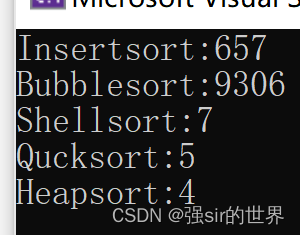
如图所示,希尔排序,堆排序和快速排序是一个量级,冒泡排序略慢
不了解堆排序和希尔排序请关注往期作品:
链接1: 希尔排序
连接2:堆排序
完整代码如下:
void Quiksort(int* a, int begin,int end)
{
//递归条件
if (begin > end)
return;
int midi = GetMidi(a, begin, end);
Swap(&a[midi], &a[begin]);
int left = begin, right = end;
int keyi = begin;
while (left < right)
{
//右边找小
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边找大
while (left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[left], &a[keyi]);
keyi = left;//更新相遇点为keyi
//递归
Quiksort(a, begin, keyi - 1);
Quiksort(a, keyi + 1, end);
}

文章来源:https://blog.csdn.net/2301_79181624/article/details/135024414
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 2024年,AI、Web3、区块链、元宇宙:有没有“相互成就“的可能性?
- C++排序算法概览
- 【PHP】 json_encode 函数各个参数的解释
- springboot中的各种下载文件的方式
- 1×1卷积层
- 上网行为管理系统,无死角监测,绝了!
- 音视频-SDL的简单使用
- C#基础——线程(线程池、线程锁、线程抢占、多线程)
- macbookpro怎么录屏?Camtasia Studio2023进行屏幕录制的方法教程
- Ant Design Vue 编译后的网页特点是什么,怎么确认他是用的前端 Ant Design Vue 技术栈的呢?