专业洞见：Python中的Statsmodels库高级线性模型

写在前面

在当今数据科学和统计分析领域，高级线性模型是解决更为复杂问题的得力工具。其中，Statsmodels库作为Python中的一项强大工具，提供了丰富的高级线性模型功能，为数据分析师和统计学家提供了更多解决方案。在本文中，我们将深入研究Statsmodels库中高级线性模型的几个重要方面，并展示它们在实际数据分析中的应用。

1 广义线性模型（GLM）

广义线性模型（Generalized Linear Model，简称GLM）是一种统计模型，适用于不同分布的响应变量。GLM的基本理念在于通过链接函数将观测数据与线性预测值关联起来。这种灵活性使得GLM能够适应多样化的数据类型，包括二项分布、泊松分布等。

1.1 GLM的基本理念

广义线性模型是线性模型的扩展，旨在解决线性模型无法直接处理的非正态分布和非恒定方差的问题。GLM 的基本理念是通过引入三个组成要素：随机分布、链接函数和系统方程，从而对广泛的数据类型建模。

GLM 的基本理念包括以下要素：

• 随机分布（Random Component）：

  • GLM 允许因变量（响应变量）服从一类更广泛的分布，不仅限于正态分布。这样，可以处理二项分布、泊松分布等不同类型的数据。
  • 随机分布的选择取决于数据的性质，例如，对于二分类问题，可以选择伯努利分布；对于计数数据，可以选择泊松分布等。

• 链接函数（Link Function）：

  • 链接函数用于将随机分布的均值与线性预测器（通常是自变量的线性组合）联系起来。
  • 链接函数的选择依赖于随机分布的性质。例如，对于伯努利分布，可以选择 logistic 函数作为链接函数；对于泊松分布，可以选择对数函数作为链接函数。

• 系统方程（System Equation）：

  • 系统方程描述了如何从自变量的线性组合得到关于均值的预测。它包括一个链接函数和一个线性预测器。
  • 系统方程的形式为：$g(\mu )=X\beta$
    其中，$g(\mu )$ 是链接函数，$\mu$是随机分布的均值，$X\beta$ 是线性预测器。

通过这三个要素的组合，GLM 能够更灵活地适应不同类型的数据，包括连续数据、二分类数据、计数数据等。同时，GLM 的最大似然估计方法能够通过迭代重加权最小二乘法（Iteratively Reweighted Least Squares，简称IRLS）来估计模型参数，从而使得模型更好地拟合非正态分布和非恒定方差的数据。GLM 的一些常见形式包括线性回归、 logistic 回归和泊松回归等。

1.2 使用Statsmodels进行GLM建模

Statsmodels库为GLM提供了直观的接口，通过合理选择链接函数和分布族，我们可以轻松构建GLM。
在使用Stasmodels进行建模时，我们一般需要增加截距项。是否添加截距项取决于具体的建模场景与数据，需要结合具体情况设定。通常，添加截距项可以帮助解释模型的截距意义，更好地拟合数据，而省略截距项则通常意味着我们知道模型中自变量的准确意义，或者我们想要使用特定方法对模型进行比较。

添加截距的方法：

import pandas as pd
import statsmodels.api as sm

# 构建测试数据
data = {'Treatment': [1, 1, 0, 1, 0, 1, 1, 1, 0, 0],
        'Recovery': [1, 1, 0, 1, 1, 1, 0, 1, 0, 0]}
df = pd.DataFrame(data)

# 方法1，使用默认方法，会自动增加一列常数项为1的截距，并命名为const
df = sm.add_constant(df)
# 方法2,自定义设置
df['Intercept'] = 1

1.2.1 使用线性回归

假设我们有一组数据，我们想用线性回归来表示学生的学习成绩（dependent variable，因变量）与学习时间（independent variable，自变量）之间的关系。

下面使用线性回归的 GLM 模型，指定了 family=sm.families.Gaussian()，表示我们使用二项分布。StudyTime 是我们的自变量，表示学习时间，而 Grades 是因变量，表示学习成绩。构建模型如下：

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 构建模拟数据
np.random.seed(12)
n_samples = 100
study_time = np.random.uniform(1, 10, n_samples)
grades = 2 * study_time + np.random.normal(0, 2, n_samples)

# 创建一个DataFrame
data = pd.DataFrame({'StudyTime': study_time, 'Grades': grades})

# 添加常数列（截距）
data = sm.add_constant(data)

# 使用GLM模型
model = sm.GLM(data['Grades'], data[['const', 'StudyTime']], family=sm.families.Gaussian())
result = model.fit()

# 打印模型摘要
print(result.summary())

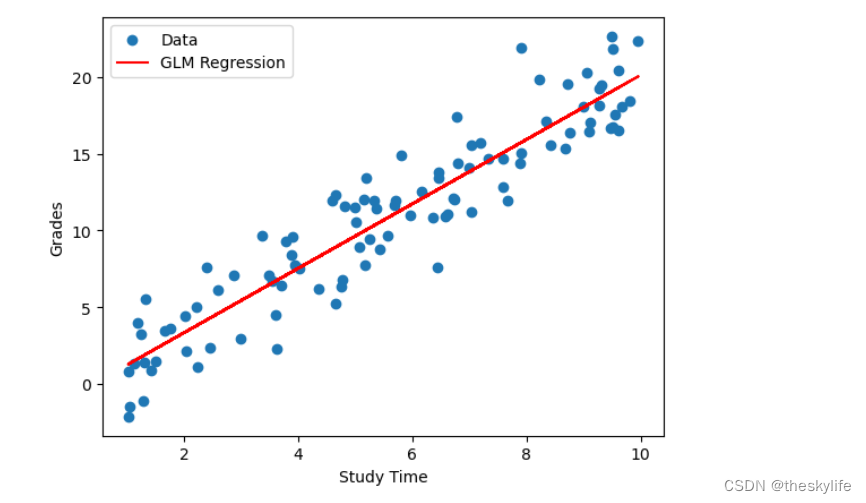
# 绘制原始数据和回归线
plt.scatter(data['StudyTime'], data['Grades'], label='Data')
plt.plot(data['StudyTime'], result.predict(), color='red', label='GLM Regression')
plt.xlabel('Study Time')
plt.ylabel('Grades')
plt.legend()
plt.show()

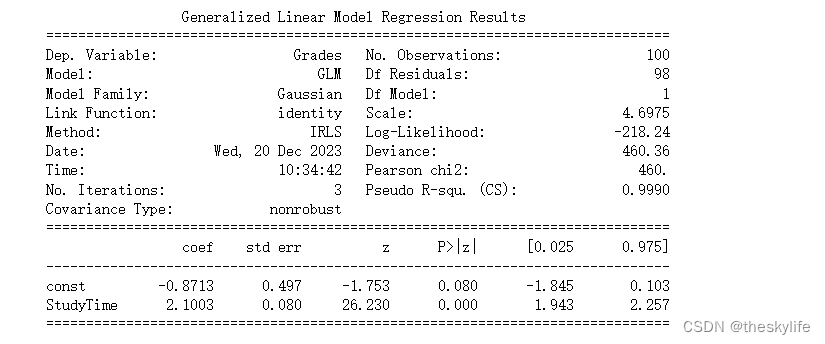
运行上述代码后，结果如下：


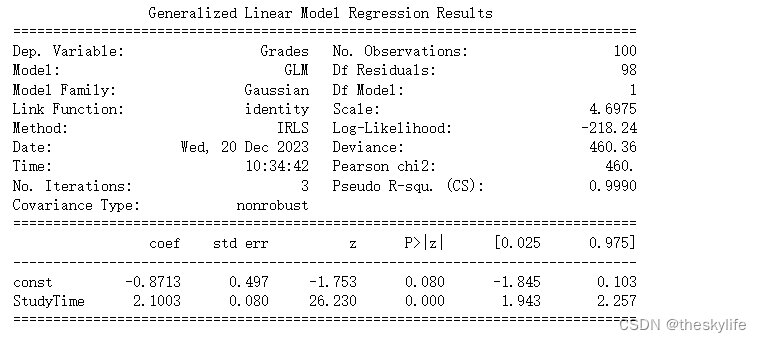
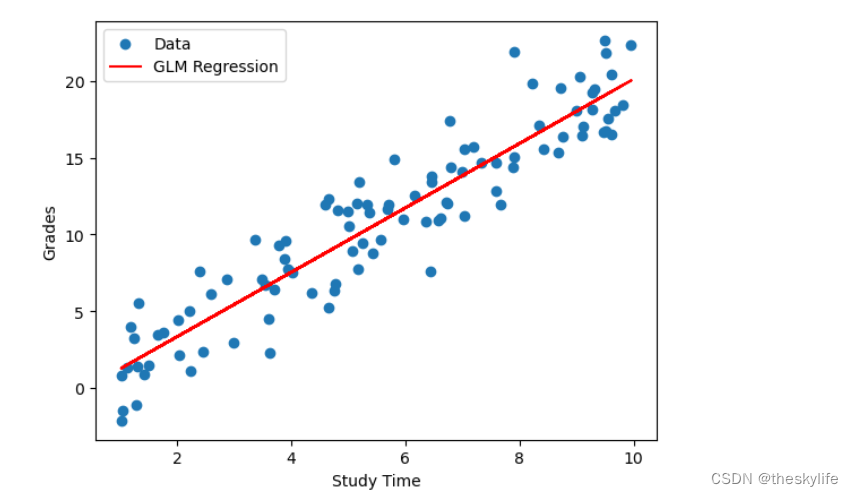
从上述结果中，我们可以得出以下结论：

1） Model Summary（模型摘要）：

• Dep. Variable（因变量）: Grades，表示我们试图预测的学生成绩。
• No. Observations（观测数量）: 100，数据集中的样本数量。
• Model Family（模型分布族）: Gaussian，表示我们使用的是正态分布作为模型的误差分布。
• Link Function（链接函数）: Identity，表示我们的模型假设是线性的。
• Method（优化方法）: IRLS，表示采用了迭代加权最小二乘法进行拟合。
• Scale（标准差）: 4.6975，正态分布的标准差。
• Pseudo R-squ. (CS)（伪R平方）: 0.9990，伪R平方值接近1，表示模型对数据的拟合非常好。

2） Coefficients（系数）:

• const（截距）: -0.8713，表示当学习时间为0时，学生成绩的预测值。
• StudyTime（学习时间）: 2.1003，表示学习时间每增加一个单位，学生成绩预测值增加的单位。

3） P-values（P值）:

• 对于const和StudyTime，P值都小于0.05，说明它们在模型中是显著的。

4） Deviance（偏差）:

• Deviance值为460.36，用于衡量模型的拟合度，数值越小表示模型拟合得越好。

模型评价:

• 由于我们生成数据时就是通过线性关系生成的，因此模型成功地捕捉到了数据中的线性关系。
• Pseudo R-squared值接近1，表明模型在这个例子中非常好地解释了数据的变化。
• 截距的P值略大于0.05，表示在5%的显著性水平下，截距并不是非常显著。

下一步思考：

• 该模型表明学生的学习时间与成绩呈线性关系，且模型拟合效果良好。
• 在实际应用中，我们可以使用这个模型来预测学生的成绩，根据学习时间调整学生的学习策略，以达到更好的学业成绩。
• 但需要注意，这只是一个简单的例子，实际场景可能涉及更多的复杂因素，需要更复杂的模型来更好地解释和预测数据。

---

1.2.2 使用logistic回归处理二分类问题

假设我们有一个医疗研究场景，研究了一种新的治疗方法对患者是否康复的影响。我们想要使用二项分布的广义线性模型（GLM）来建模，以了解治疗方法对康复概率的影响。

场景：
医疗研究中，研究新治疗方法是否能够提高患者康复的概率。

数据：
我们有一组患者的数据，每个患者都接受了新治疗方法，并记录了他们是否康复的结果。康复与否用二元变量表示，1 表示康复，0 表示未康复。

下面使用二项分布的 GLM 模型，指定了 family=sm.families.Binomial()，表示我们使用二项分布。Treatment 是我们的自变量，表示是否接受了新治疗方法，而 Recovery 是二元的因变量，表示是否康复

import pandas as pd
import statsmodels.api as sm

# 构建模拟数据
data = {'Treatment': [1, 1, 0, 1, 0, 1, 1, 1, 0, 0],
        'Recovery': [1, 1, 0, 1, 1, 1, 0, 1, 0, 0]}
df = pd.DataFrame(data)

# 添加截距项
df['Intercept'] = 1

# 创建 logistic 回归模型
logit_model = sm.GLM(df['Recovery'], df[['Intercept', 'Treatment']], family=sm.families.Binomial())
# 拟合模型
result = logit_model.fit()
# 打印模型摘要
print(result.summary())

运行上述代码后，得出结果如下：

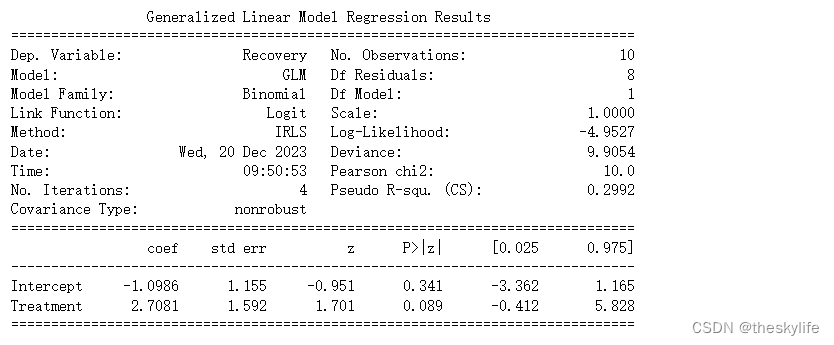
根据上方的运行结果，我们可以得出下面的结论：

1). 模型系数（Coefficients）：

• Intercept 的系数为 -1.0986，表示在 Treatment 变量为 0 时，即未接受新治疗方法时，康复的 log-odds（对数几率）为 -1.0986。
• Treatment 的系数为 2.7081，表示接受新治疗方法相对于未接受的情况下，康复的 log-odds 增加了 2.7081。

2). P-值（P>|z|）：

• 对于 Intercept 的 P-值为 0.341，Treatment 的 P-值为 0.089。通常，我们使用显著性水平 0.05，如果 P-值小于 0.05，则认为对应的系数是显著的。
• 在这个例子中，Treatment 的 P-值为 0.089 大于 0.05，表示在统计学上没有足够的证据拒绝 Treatment 对康复概率的影响为零的假设。

3). 伪 R-squared（Pseudo R-squ.）：

• 伪 R-squared 衡量了模型的拟合优度。在这个例子中，伪 R-squared（CS）为 0.2992，表示模型能够解释目标变量 29.92% 的变异性。

4). 对数似然（Log-Likelihood）：

• 对数似然为 -4.9527，是模型对观察到的数据的拟合程度的一个指标。对数似然越高，模型拟合越好。

5). Deviance 和 Pearson chi2：

• Deviance 衡量了模型的拟合优度，值越小表示拟合越好。Pearson chi2 则表示模型的卡方拟合度，也是拟合好坏的一个指标。在这个例子中，Deviance 为 9.9054，Pearson chi2 为 10.0。

模型整体概括：

• 由于 Treatment 变量的 P-值（0.089）较大，不能拒绝 Treatment 对康复概率的影响为零的假设。在统计学上，这意味着我们没有足够的证据表明接受新治疗方法会显著地增加患者康复的概率。
• 伪 R-squared（CS）为 0.2992，表明模型对康复与否的变异性解释度相对较低。

下一步思考：

• 结果提醒我们，治疗方法的效果在这个小样本中没有显著性。但是，小样本可能限制了我们对真实效果的探究。
• 如果研究的样本量增加，可能会有更强的统计证据，从而更好地评估治疗方法对康复概率的影响。
• 此外，可能还需要考虑其他变量，如患者的基线特征，以更全面地了解治疗方法的效果。

在实际应用中，建议根据模型结果综合考虑，谨慎解释，尤其是在小样本情况下。模型的解释力受到样本大小和其他潜在变量的限制。

---

2 高级线性混合效应模型

高级线性混合效应模型（Hierarchical Linear Mixed Effects Models，简称HLM或者LMM）是线性混合效应模型（Mixed Effects Models）的一种扩展。它在统计建模中应用广泛，特别是在处理具有层次结构或重复测量的数据时。

这种模型通常包含两个层次的随机效应：一个是在个体水平的随机效应，另一个是在群体水平的随机效应。这使得HLM能够同时考虑个体差异和群体之间的差异。

HLM的特点包括以下几个：

• 层次结构： 数据被组织成多个层次，例如个体嵌套在群体中，或者多次测量嵌套在个体中。

• 固定效应： 模型包含固定效应，用于解释自变量对因变量的影响。这些固定效应通常是我们感兴趣的参数，用于推断总体关系。

• 随机效应： 模型包含随机效应，用于捕捉个体或群体的随机变异。这使得模型能够处理个体差异和群体差异。

• 方差分解： HLM能够分解总体方差为个体水平和群体水平的方差，这对于理解不同层次上的变异结构非常有用。

• 融合信息： HLM允许从高层次（群体）到低层次（个体）传递信息，提高对个体效应的估计精度。

• 模型的层次： 模型可以有多个层次，具体取决于数据的层次结构。例如，可以有三层模型，包含观测、个体和群体层次。

HLM的公式通常形式如下：

$Y_{ij}=X_{ij}\beta +Z_{ij}{b}_j+{\epsilon }_{ij}$

其中：

• $Y_{ij}$ 是第 $i$ 个个体在第 $j$ 个群体中的观测值。
• $X_{ij}$ 是第 $i$ 个个体在第 $j$ 个群体中的固定效应设计矩阵。
• $\beta$ 是固定效应的参数向量。
• $Z_{ij}$ 是第 $i$ 个个体在第 $j$ 个群体中的随机效应设计矩阵。
• $b_j$ 是第 $j$ 个群体的随机效应向量。
• ${\epsilon }_{ij}$ 是第 $i$ 个个体在第 $j$ 个群体中的残差。

需要注意的是，HLM的使用需要谨慎，尤其是在数据较少的情况下，需要小心过拟合问题。此外，模型的建立需要考虑研究问题的特点和目标，以及对模型中参数的解释需求。

2.1 高级线性混合效应模型的应用场景

根据高级线性混合效应模型（HLM）的特点情况，我们通常在以下情况下考虑使用：

• 层次结构： 当研究数据具有层次结构，即观测单位（例如个体）嵌套在更高级别的群体或集群中时，HLM是一种适用的方法。例如，学生嵌套在不同的学校中，或者个体嵌套在家庭中。

• 随机效应： 当我们关心个体之间的变异性，且这种变异性无法完全由固定效应解释时，可以引入随机效应。HLM允许我们在模型中同时考虑固定效应和随机效应，更全面地捕捉数据的结构。

• 融合信息： HLM允许从高层次（群体）到低层次（个体）传递信息，以提高对个体效应的估计精度。这种信息的传递有助于更好地估计个体之间的差异。

• 处理重复测量： 当数据包含重复测量或者纵向观察时，HLM是一种处理相关性和时间依赖性的强大工具。它可以考虑观测之间的相关性，允许建模时间趋势和变异性。

• 控制混淆： 当研究中存在未观察到的混淆因素，而这些混淆因素可能在群体层次上产生影响时，HLM可以用来控制这些混淆因素的影响。

• 研究过程的随机性： 在一些研究中，过程本身可能具有随机性。HLM允许考虑这种随机性，以更好地理解和解释观测结果。

• 模型的复杂性： 当研究问题需要考虑多层次、多水平的因素时，HLM提供了一个灵活的框架，可以更精确地建模这种复杂性。

需要注意的是，HLM的使用需要谨慎，尤其是在数据较少的情况下，需要小心过拟合问题。此外，模型的建立需要考虑研究问题的特点和目标，以及对模型中参数的解释需求。

场景举例：

1).教育研究： 学生嵌套在不同的学校中，教育研究中常常使用HLM来分析学生在学校和班级层次上的学业表现。

2).医学研究： 患者嵌套在不同的医院或医生中，HLM可用于分析患者在医疗机构层次上的响应变量，考虑到患者之间可能存在的差异。

3).组织行为学研究： 员工嵌套在不同的团队或部门中，研究员工绩效或工作满意度时，HLM可以考虑到团队或部门层次上的变异。

4).社会调查： 调查数据中可能包含了个体嵌套在不同的地理区域中，HLM可以用于考虑地理区域对调查结果的影响。

5).心理学实验： 在实验中，被试可能被分配到不同的实验条件或组别，HLM可以用于分析实验条件对被试反应的影响。

6).家庭研究： 家庭成员嵌套在不同的家庭中，HLM可以用于研究家庭因素对个体行为的影响。

7).公共卫生研究： 个体嵌套在不同的社区或地理区域中，研究社区因素对健康状况的影响时，HLM可以帮助考虑社区层次上的变异。

8).长期研究或纵向研究： 当数据包含多次测量或观察时，HLM可以用于建模时间趋势和考虑观察之间的相关性。

9).行为经济学研究： 在研究经济决策时，个体可能受到不同的市场、城市或公司的影响，HLM可以用于建模这些层次结构。

10).多层次实验设计： 在多层次实验中，实验单元（例如学生、班级、学校）嵌套在不同的层次中，HLM可以用于分析实验条件对实验单元的影响。

2.2 利用Statsmodels进行高级线性混合效应建模

假设我们现在关注的是体育赛事中运动员的表现，我们想了解运动员的体重、训练时长以及他们所属的训练组对于比赛成绩的影响。此外，我们考虑到运动员可能在不同的训练组中受到一些特定的随机效应。现在构建模型如下：

import numpy as np
import pandas as pd
import statsmodels.api as sm

np.random.seed(123)

# 创建示例数据集
num_students = 500
num_schools = 50

# 生成学校数据
school_data = pd.DataFrame({
    'SchoolID': range(1, num_schools + 1),
    'SchoolQuality': np.random.normal(0, 1, num_schools)  # 学校教学质量
})

# 生成学生数据，并为每个学生分配一个学校ID
student_data = pd.DataFrame({
    'StudentID': range(1, num_students + 1),
    'MathScore': np.random.normal(70, 10, num_students),
    'StudyTime': np.random.normal(5, 2, num_students),
    'FamilyBackground': np.random.choice(['High', 'Low'], num_students),
    'SchoolID': np.random.choice(range(1, num_schools + 1), num_students)
})

# 合并学生和学校数据
data = pd.merge(student_data, school_data, on='SchoolID')

# 构建高级线性混合效应模型
formula = 'MathScore ~ StudyTime * FamilyBackground + SchoolQuality'
model = sm.MixedLM.from_formula(formula, data, groups=data['SchoolID'])
# result = model.fit(maxiter=1000)
result = model.fit(maxiter=1000,method='lbfgs')  # 例如，尝试使用LBFGS优化算法

# 打印模型摘要
print(result.summary())

# 构建高级线性混合效应模型
formula = 'Performance ~ Weight + TrainingDuration + GroupEffect + (1 | AthleteID)'
model = sm.MixedLM.from_formula(formula, data, groups=data['GroupID'])
result = model.fit()

# 打印模型摘要
print(result.summary())

运行上述代码后，我们得到结果如下：

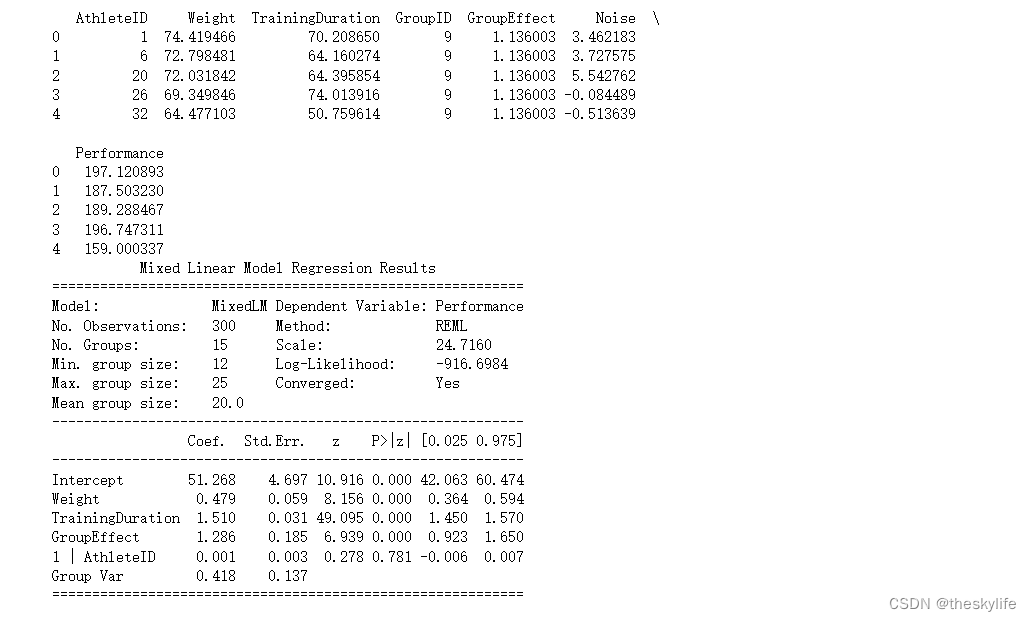
从上述结果中，我们可以得出以下信息：

• 固定效应（Fixed Effects）：

  • Intercept（截距）： 截距为51.268，表示在体重、训练时长和训练组效应都为0的情况下，预测的平均表现分数。
  • Weight： 体重的系数为0.479，表示每增加1单位的体重，表现分数增加0.479分。
  • TrainingDuration： 训练时长的系数为1.510，表示每增加1单位的训练时长，表现分数增加1.510分。
  • GroupEffect： 训练组效应的系数为1.286，表示在其他因素不变的情况下，属于某个训练组的运动员平均比其他运动员表现好1.286分。

• 随机效应（Random Effects）：

  • 1 | AthleteID： 运动员的随机效应的方差为0.001，这个值较小，可能说明运动员之间的随机差异不是很大。

• 模型拟合情况：

  • No. Observations： 观察数为300。
  • No. Groups： 训练组的数量为15。
  • Mean group size： 平均每个训练组的运动员数量为20.0。
  • Converged： 模型是否收敛。在这个输出中，收敛为 “Yes”，表示模型在拟合时达到了收敛。

• 解释变量的影响：

  • 各项系数的p-value都非常小，小于通常接受的显著性水平0.05，表示它们对表现分数的影响是显著的。

实际场景应用：

1).预测运动员表现： 使用训练好的模型，根据具体的体重、训练时长和所属训练组等信息，可以预测某个运动员的比赛表现。例如，给定一个运动员的体重、训练时长和训练组，可以通过模型预测其预期的比赛成绩。

# 假设有一个新的运动员的信息
new_athlete = pd.DataFrame({
    'Weight': [75],
    'TrainingDuration': [65],
    'GroupEffect': [0],  # 在预测时，随机效应可以设置为0
    'AthleteID': [num_athletes + 1]  # 随便给一个新的AthleteID
})

# 使用模型进行预测
predicted_performance = result.predict(new_athlete)
print("预测的比赛成绩：", predicted_performance.values[0])

根据模型预测效果，得出该运动员的预测比赛成绩： 185.6078526165864

2).影响因素的重要性： 可以通过查看模型的系数来评估每个变量对表现分数的相对重要性。如该模型中，影响程度由高至低依次为训练时长、训练组、体重。

3).个体差异和组差异： 通过模型输出的随机效应部分，可以了解个体差异（AthleteID的方差）和训练组差异（Group Var）。本例中个体差异较小，说明模型在考虑体重、训练时长和训练组的情况下已经很好地解释了运动员之间的差异。

---

3 泊松回归

泊松回归是一种广义线性模型的一种形式，用于建模计数数据的回归分析。它通常用于描述某个时间或空间单位内发生的事件次数，例如交通事故、疾病发病次数、电话呼叫次数等。

泊松回归的基本假设是事件在时间或空间单位内以固定的平均发生率发生，且事件的发生是独立的。泊松回归模型的数学表达式如下：

$\ln (\lambda )={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{x}_k$

其中：

• $\ln (\lambda )$ 是事件发生的对数期望值，也称为线性预测值。
• ${\beta }_0$ 是截距，表示当所有自变量为零时事件发生的对数期望值。
• ${\beta }_1,{\beta }_2,\dots ,{\beta }_k$ 是自变量的系数，表示每个自变量对事件发生的影响。
• $x_1,x_2,\dots ,x_k$ 是自变量的取值。

泊松回归的关键特点包括：

• 计数数据： 适用于离散的计数数据，即每个单位内发生的事件次数是非负整数。

• 假设： 泊松回归假设事件在单位内以固定的平均发生率发生，并且事件之间是独立的。

• 自然对数链接函数： 为了确保预测值是正的，泊松回归使用自然对数链接函数，将线性组合映射到正实数域。

• 拟合度： 模型拟合度可通过观测到的事件次数与模型预测的事件次数的比较来评估。

• 偏差： 由于事件发生次数通常具有泊松分布的特征，模型中的偏差（残差）通常也应该服从泊松分布。

3.1 解释泊松回归的应用场景

泊松回归适用于一系列特定的条件，主要包括：

1).计数数据： 泊松回归适用于离散的计数数据，其中每个观察单位都是一个计数，例如事件发生的次数。

2).独立性： 事件在不同的单位（时间、空间等）内的发生应是相互独立的。

3).恒定的发生率： 泊松回归假设在不同的单位内，事件的发生概率是恒定的。

4). 整数值输出： 泊松回归的输出是整数值，因为它描述的是事件发生的次数。

在实际应用中，泊松回归适用于以下几个场景：

• 交通事故预测： 泊松回归可以用于预测某地区在一段时间内的交通事故次数，考虑到交通事故通常是离散事件。

• 疾病发病率： 用于研究某种疾病在不同地区或时间内的发病次数，尤其在罕见事件的情况下。

• 电话呼叫量预测： 泊松回归可用于预测一个服务中心在一天内接收的电话呼叫次数。

• 生态学研究： 用于研究生态系统中某种动植物的数量，考虑到它们的数量通常是整数。

• 网络流量分析： 用于分析网络上的数据包传输次数，考虑到传输次数是离散的。

选择合适的自变量是泊松回归分析中的一个关键步骤，它直接影响模型的解释性和预测能力。实际运用过程中可以通过问题的理论基础、探索性数据分析、领域专家意见、信息准则、交叉验证、避免多重共线性等方法来选择合适的自变量。
选择合适的自变量是一个既考验经验又需要一定科学方法的过程。结合领域知识、实际数据分析和模型评估，有助于得到一个在实际场景中具有解释力和预测能力的泊松回归模型。

3.2 使用Statsmodels进行泊松回归建模

下面将通过一个实际场景来使用Statsmodels进行泊松回归的广义线性模型（GLM）建模。假设我们想要分析一天内发生的交通事故数量与某个城市的交通密度之间的关系。
下面使用泊松的 GLM 模型，指定了 family=sm.families.Poisson()，表示我们使用泊松分布。TrafficDensity 是我们的自变量，表示交通密度，而 Accidents 是因变量，表示交通事故发生的数量。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# 构建模拟数据
np.random.seed(12)
n_days = 30
traffic_density = np.random.uniform(50, 200, n_days)
accidents = np.random.poisson(traffic_density * 0.1, n_days)

# 创建一个DataFrame
data = pd.DataFrame({'TrafficDensity': traffic_density, 'Accidents': accidents})

# 添加常数列（截距）
data = sm.add_constant(data)

# 使用GLM模型，指定family='Poisson'
model = sm.GLM(data['Accidents'], data[['const', 'TrafficDensity']], family=sm.families.Poisson())
result = model.fit()

# 打印模型摘要
print(result.summary())

# 绘制原始数据和回归线
plt.scatter(data['TrafficDensity'], data['Accidents'], label='Data')
plt.plot(data['TrafficDensity'], result.predict(), color='red', label='Poisson Regression')
plt.xlabel('Traffic Density')
plt.ylabel('Accidents')
plt.legend()
plt.show()

运行上述代码后，运行结果如下：

通过上述的结果，我们可以得出以下信息：

1). Model Summary（模型摘要）：

• Dep. Variable（因变量）: Accidents，表示我们试图预测的一天内交通事故的数量。
• No. Observations（观测数量）: 30，数据集中的天数。
• Model Family（模型分布族）: Poisson，表示我们使用的是泊松分布作为模型的误差分布。
• Link Function（链接函数）: Log，表示我们的模型假设是对数线性的。
• Method（优化方法）: IRLS，表示采用了迭代加权最小二乘法进行拟合。
• Scale（标准差）: 1.0000，泊松分布的标准差。
• Pseudo R-squ. (CS)（伪R平方）: 0.9337，伪R平方值接近1，表示模型对数据的拟合非常好。

2). Coefficients（系数）:

• const（截距）: 1.2379，表示当交通密度为0时，一天内交通事故的预测值。
• TrafficDensity（交通密度）: 0.0100，表示交通密度每增加一个单位，一天内交通事故数量预测值的变化。

3). P-values（P值）:

• 对于const和TrafficDensity，P值都小于0.05，说明它们在模型中是显著的。

4). Deviance（偏差）:

• Deviance值为41.881，用于衡量模型的拟合度，数值越小表示模型拟合得越好。

模型评价:

• 由于我们使用泊松分布来模拟交通事故的发生次数，该模型考虑到了离散计数数据的特性。
• Pseudo R-squared值接近1，表明模型在这个例子中非常好地解释了数据的变化。
• 截距的P值和系数的P值均小于0.05，表示这两个变量在模型中是显著的。

在实际场景中的运用：

• 该模型可用于理解交通密度对交通事故发生率的影响，并预测未来某天的交通事故数量。
• 通过调整交通密度，该模型中TrafficDensity的系数为正，增加交通密度可能会导致预测的交通事故数量上升，反之亦然。因此，城市交通管理者可以优化交通流，减少车流量，从而降低交通密度，以减少交通事故的发生。
• 注意，实际应用中可能需要更多的特征和更多的数据，以提高模型的准确性和泛化能力。

一个实际的预测

# 假设未来某一天的交通密度
future_traffic_density = 200

# 使用模型预测未来某一天的交通事故数量
predicted_accidents = result.predict([1, future_traffic_density])[0]
# 打印预测的值
print(f"预测未来某一天的交通事故数量：{predicted_accidents:.0f}")

利用上述的代码，我们得出未来某一天的交通密度为200时，交通事故的数量为26。

写在最后

通过本文的介绍，我们深入了解了Statsmodels库在高级线性模型中的应用。从广义线性模型、高级线性混合效应模型到泊松回归，Statsmodels提供了丰富的工具，帮助我们更好地理解和解决复杂的数据分析问题。在实际应用中，选择合适的模型和正确解释结果对于取得可靠的洞见至关重要。希望本文能够帮助读者更好地利用Statsmodels库进行高级线性模型的建模和分析。