【GA MTSP】遗传算法求解多旅行商问题（多且同始终点）【含Matlab源码 1339期】

?一、获取代码方式

获取代码方式1：
完整代码已上传我的资源：【MTSP】基于matlab遗传算法求解多旅行商问题【含Matlab源码 1339期】

获取代码方式2：
付费专栏Matlab路径规划（初级版）

备注：
点击上面蓝色字体付费专栏Matlab路径规划（初级版），扫描上面二维码，付费29.9元订阅海神之光博客付费专栏Matlab路径规划（初级版），凭支付凭证，私信博主，可免费获得1份本博客上传CSDN资源代码（有效期为订阅日起，三天内有效）；
点击CSDN资源下载链接：1份本博客上传CSDN资源代码

?二、TSP简介

旅行商问题，即TSP问题（Traveling Salesman Problem）又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
TSP的数学模型

?三、遗传算法简介

1 引言


2 遗传算法理论
2.1 遗传算法的生物学基础


2.2 遗传算法的理论基础




2.3 遗传算法的基本概念






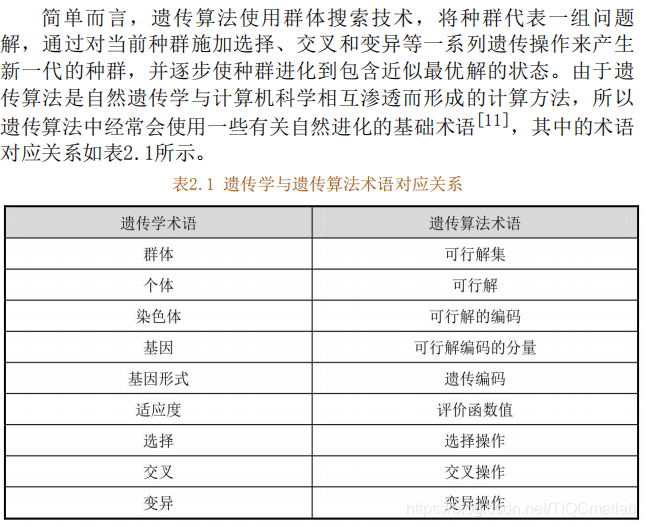
2.4 标准的遗传算法


2.5 遗传算法的特点


2.6 遗传算法的改进方向

3 遗传算法流程



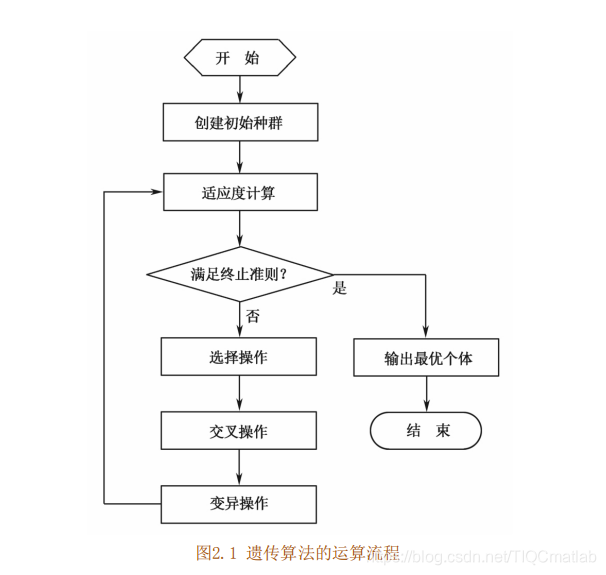
4 关键参数说明

?四、部分源代码

function [min_dist,best_tour,generation] = mdmtspv_ga(xy,max_salesmen,depots,CostType,min_tour,pop_size,num_iter,show_prog,show_res,dmat)
% MDMTSPV_GA Multiple Depots Multiple Traveling Salesmen Problem (M-TSP)
% with Variable number of salesmen using Genetic Algorithm (GA)
% Finds a (near) optimal solution to a variation of the M-TSP (that has a
% variable number of salesmen) by setting up a GA to search for the
% shortest route (least distance needed for the salesmen to travel to
% each city exactly once and return to their starting locations). The
% salesmen originate from a set of fixed locations, called depots.
% This algorithm is based on Joseph Kirk’s MTSPV_GA, but adds the
% following functionality:
% 1. Depots at which each salesman originates and ends its tour.
% 2. Two possible cost functions, that allow to find minimum sum of all
% tour lengths (as in the original version) and to find the minimum
% longest tour. The latter problem is sometimes called MinMaxMDMTSP.
%
% Summary:
% 1. Each salesman travels to a unique set of cities and completes the
% route by returning to the depot he started from
% 2. Each city is visited by exactly one salesman
%
% Input:
% XY (float) is an Nx2 matrix of city locations, where N is the number of cities
% max_salesmen (scalar integer) is the maximum number of salesmen
% depots (float) ia an Mx2 matrix of the depots used by salesmen, M=max_salesmen
% CostType (integer) defines which cost we use. If 1 - sum of all route lengths, if 2 - maximum route length% MIN_TOUR (scalar integer) is the minimum tour length for any of the salesmen
% POP_SIZE (scalar integer) is the size of the population (should be divisible by 16)
% NUM_ITER (scalar integer) is the number of desired iterations for the
% algorithm to run after a new best solution is found. Don’t worry the
% algorithm will always stop.
% SHOW_PROG (scalar logical) shows the GA progress if true
% SHOW_RES (scalar logical) shows the GA results if true
% DMAT (float) is an NxN matrix of point to point distances or costs

%
% Output:
% MIN_DIST (scalar float) is the best cost found by the algorithm
% BEST_TOUR (matrix integer) is an MxL matrix, each row is an agent tour
% Generation (scalar integer) is the number of generations required by
% the algorithm to find the solution

%
% Route/Breakpoint Details:
% The algorithm uses a data structure in which RTE lists the cities in
% a route and BRKS lists break points that divide RTE between agents.
% If there are 10 cities and 3 salesmen, a possible route/break
% combination might be: rte = [5 6 9 1 4 2 8 10 3 7], brks = [3 7]
% Taken together, these represent the solution [5 6 9][1 4 2 8][10 3 7],
% which designates the routes for the 3 salesmen as follows:
% . Salesman 1 travels from city 5 to 6 to 9 and back to 5
% . Salesman 2 travels from city 1 to 4 to 2 to 8 and back to 1
% . Salesman 3 travels from city 10 to 3 to 7 and back to 10
% Note that the salesman’s depot will be taken into accout, so the
% complete routes returned by the algorithm will be:
% For agent 1: [1 5 6 9 1] - from depot 1 along the route and back
% For agent 2: [2 1 4 2 8 2] - from depot 2 along the route and back
% For agent 3: [3 10 3 7 3] - from depot 3 along the rout and back
%
% 2D Example:
% n = 35;
% xy = 10rand(n,2);
% max_salesmen = 5;
% depots = 10rand(max_salesmen,2);
% CostType=1; %- total length, use 2 to minimize the longest tour
% min_tour = 3;
% pop_size = 80;
% num_iter = 1e3;
% a = meshgrid(1:n);
% dmat = reshape(sqrt(sum((xy(a,:)-xy(a’😅).^2,2)),n,n);
% [min_dist,best_tour,generation] = mdmtspv_ga(xy,max_salesmen,depots,CostType,min_tour,pop_size,num_iter,1,1,dmat)
%
% 3D Example:
% n = 35;
% xy = 10rand(n,3);
% max_salesmen = 5;
% depots = 10rand(max_salesmen,3);
% CostType=1; %- total length, use 2 to minimize the longest tour
% min_tour = 3;
% pop_size = 80;
% num_iter = 1e3;
% a = meshgrid(1:n);
% dmat = reshape(sqrt(sum((xy(a,:)-xy(a’😅).^2,2)),n,n);
% [min_dist,best_tour,generation] = mdmtspv_ga(xy,max_salesmen,depots,CostType,min_tour,pop_size,num_iter,1,1,dmat)
%
% See also: mtsp_ga, mtspf_ga, mtspo_ga, mtspof_ga, mtspofs_ga, distmat

% Process Inputs and Initialize Defaults
nargs = 10;
for k = nargin:nargs-1
switch k
case 0
xy = 10rand(40,2);
case 1
max_salesmen=10;
case 2
depots = 10rand(max_salesmen,2);
case 3
CostType = 2;
case 4
min_tour = 1;
case 5
pop_size = 80;
case 6
num_iter = 1e3;
case 7
show_prog = 1;
case 8
show_res = 1;
case 9
N = size(xy,1);
a = meshgrid(1:N);
dmat = reshape(sqrt(sum((xy(a,:)-xy(a’😅).^2,2)),N,N);
otherwise
end
end

Epsilon=1e-10;

% Distances to Depots
%Assumes that each salesman is located at a different depot and there are
%enough depots
[NumOfCities,Dimensions]=size(xy);
for i=1:max_salesmen
for j=1:NumOfCities
D0(i,j)=norm(depots(i,:)-xy(j,:));
end
end

% Verify Inputs
[N,dims] = size(xy);
[nr,nc] = size(dmat);
if N ~= nr || N ~= nc
error(‘Invalid XY or DMAT inputs!’)
end
n = N;

% Sanity Checks
min_tour = max(1,min(n,round(real(min_tour(1)))));
pop_size = max(8,8*ceil(pop_size(1)/8));
num_iter = max(1,round(real(num_iter(1))));
show_prog = logical(show_prog(1));
show_res = logical(show_res(1));

% Initialize the Populations
pop_rte = zeros(pop_size,n); % population of routes
pop_brk = cell(pop_size,1); % population of breaks
for k = 1:pop_size
pop_rte(k,:) = randperm(n);
pop_brk{k} = randbreak(max_salesmen,n,min_tour);
end

% Select the Colors for the Plotted Routes
%clr = hsv(ceil(n/min_tour));
clr = hsv(max_salesmen);

% Run the GA
global_min = Inf;
total_dist = zeros(1,pop_size);
dist_history = zeros(1,num_iter);
tmp_pop_rte = zeros(8,n);
tmp_pop_brk = cell(8,1);
new_pop_rte = zeros(pop_size,n);
new_pop_brk = cell(pop_size,1);
if show_prog
pfig = figure(‘Name’,‘MTSPV_GA | Current Best Solution’,‘Numbertitle’,‘off’);
end
iter=0;
iter2go=0;
while iter2go < num_iter
iter2go=iter2go+1;
iter=iter+1;
% Evaluate Each Population Member (Calculate Total Distance)
for p = 1:pop_size
d = [];
p_rte = pop_rte(p,:);
p_brk = pop_brk{p};
salesmen = length(p_brk)+1;
rng=CalcRange(p_brk,n);
for sa = 1:salesmen
if rng(sa,1)<=rng(sa,2)
Tour=[sa p_rte(rng(sa,1):rng(sa,2)) sa];
indices=length(Tour)-1;
d(sa)=CalcTourLength(Tour,dmat,D0,indices);
else
Tour=[sa sa];
d(sa)=0;
end
end
if CostType1
total_dist§ = sum(d);
elseif CostType2
total_dist§ = max(d)+Epsilon*sum(d);
end
end

% Find the Best Route in the Population
[min_dist,index] = min(total_dist);
dist_history(iter) = min_dist;
if min_dist < global_min
    iter2go=0;
    generation=iter;
    global_min = min_dist;
    opt_rte = pop_rte(index,:);
    opt_brk = pop_brk{index};
    salesmen = length(opt_brk)+1;
    rng=CalcRange(opt_brk,n);
    if show_prog
        % Plot the Best Route
        figure(pfig);
        clf
        for s = 1:salesmen
            if dims==2
                plot(depots(s,1),depots(s,2),'s','Color',clr(s,:));
            else
                plot3(depots(s,1),depots(s,2),depots(s,3),'s','Color',clr(s,:));
            end
            if rng(s,1)<=rng(s,2)
                rte = opt_rte([rng(s,1):rng(s,2)]);
                hold on;
                if ~isempty(rte) && dims == 2
                    plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:));                                    
                    plot([depots(s,1),xy(rte(1),1)],[depots(s,2),xy(rte(1),2)],'Color',clr(s,:));
                    plot([depots(s,1),xy(rte(end),1)],[depots(s,2),xy(rte(end),2)],'Color',clr(s,:));
                elseif ~isempty(rte) && dims == 3
                    plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:));                                    
                    plot3([depots(s,1),xy(rte(1),1)],[depots(s,2),xy(rte(1),2)],[depots(s,3),xy(rte(1),3)],'Color',clr(s,:));
                    plot3([depots(s,1),xy(rte(end),1)],[depots(s,2),xy(rte(end),2)],[depots(s,3),xy(rte(end),3)],'Color',clr(s,:));
                end                    
            end
            title(sprintf(['Total Distance = %1.4f, Salesmen = %d, ' ...
                'Iteration = %d'],min_dist,salesmen,iter));
            hold on
        end
        pause(0.02)
        hold off
    end
end 

?五、运行结果

?六、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]王海龙,周辉仁,郑丕谔,唐万生.基于遗传算法的多旅行商问题研究[J].计算机应用研究. 2009,26(05)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除