代码随想录算法训练营第二十七天|组合总和等
发布时间:2023年12月25日
77 组合
1 描述
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
2 代码
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
path = []
rst = []
def helper(start):
end = n + 1 - (k - len(path) - 1)
for i in range(start, end):
path.append(i)
if len(path) == k:
rst.append(path[:])
else:
helper(i + 1)
path.pop()
return
helper(1)
return rst?3 总结?
- python 的参数传递,参考Python里参数是值传递还是引用传递? - 知乎 (zhihu.com)
- global 关键字 与 nonlocal 关键字的用法(主要针对不可变对象)?
?216.组合总和III
1 描述
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]
示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]
2 代码
class Solution:
def __init__(self):
self.path = []
self.sum_ = 0
self.rst = []
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
def helper(start):
end = 10 - (k - len(self.path) - 1)
for i in range(start, end):
self.path.append(i)
self.sum_ += i
if len(self.path) == k and self.sum_ == n:
self.rst.append(self.path[:])
elif len(self.path) < k and self.sum_ < n:
helper(i + 1)
self.path.pop()
self.sum_ -= i
return
helper(1)
return self.rst17.电话号码的字母组合
1 描述
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
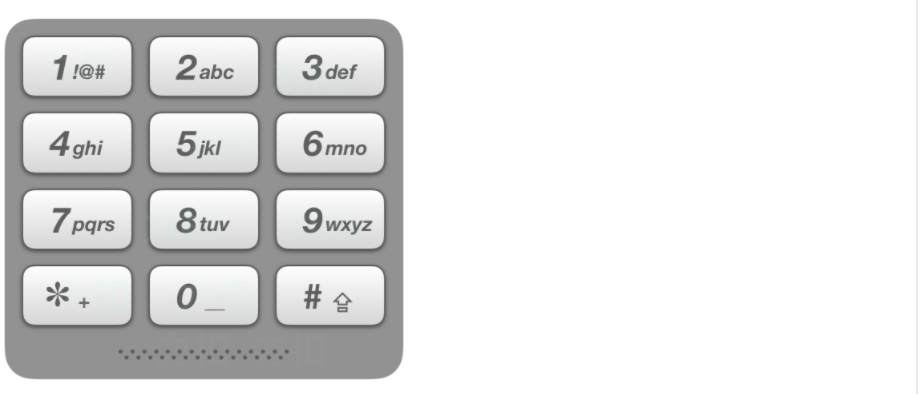
示例:
- 输入:"23"
- 输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
2 代码
class Solution:
def __init__(self):
self.d = {
'2':['a', 'b', 'c'],
'3':['d', 'e', 'f'],
'4':['g', 'h', 'i'],
'5':['j', 'k', 'l'],
'6':['m', 'n', 'o'],
'7':['p', 'q', 'r', 's'],
'8':['t', 'u', 'v'],
'9':['w', 'x', 'y', 'z'],
}
self.path = []
self.rst = []
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
def helper(i):
if i == len(digits):
self.rst.append(''.join(self.path))
return
for c in self.d[digits[i]]:
self.path.append(c)
helper(i + 1)
self.path.pop()
helper(0)
return self.rst39. 组合总和
1 描述
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
- 输入:candidates = [2,3,6,7], target = 7,
- 所求解集为: [ [7], [2,2,3] ]
示例 2:
- 输入:candidates = [2,3,5], target = 8,
- 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]
2 代码
class Solution:
def __init__(self):
self.path = []
self.sum_ = 0
self.rst = []
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def helper(start):
for i in range(start, len(candidates)):
self.path.append(candidates[i])
self.sum_ += candidates[i]
if self.sum_ < target:
helper(i)
elif self.sum_ == target:
self.rst.append(self.path[:])
self.path.pop()
self.sum_ -= candidates[i]
return
helper(0)
return self.rst40.组合总和II
1 描述
给定一个候选人编号的集合?candidates?和一个目标数?target?,找出?candidates?中所有可以使数字和为?target?的组合。
candidates?中的每个数字在每个组合中只能使用?一次?。
注意:解集不能包含重复的组合。?
示例?1:
输入: candidates =?[10,1,2,7,6,1,5], target =?8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ]
示例?2:
输入: candidates =?[2,5,2,1,2], target =?5, 输出: [ [1,2,2], [5] ]
提示:
1 <=?candidates.length <= 1001 <=?candidates[i] <= 501 <= target <= 30
2 代码
class Solution:
def __init__(self):
self.path = []
self.rst = []
self.sum_ = 0
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
def helper(start):
for i in range(start, len(candidates)):
if i > start and candidates[i] == candidates[i - 1]:
continue
self.path.append(candidates[i])
self.sum_ += candidates[i]
if self.sum_ == target:
self.rst.append(self.path[:])
elif self.sum_ < target:
helper(i + 1)
else:
self.path.pop()
self.sum_ -= candidates[i]
break
self.path.pop()
self.sum_ -= candidates[i]
helper(0)
return self.rst?
文章来源:https://blog.csdn.net/cui_15/article/details/135208891
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 在set容器中利用find()和end()查找元素的简单使用
- PyTorch深度学习实战(20)——从零开始实现Fast R-CNN目标检测
- 【无标题】
- zabbix自定义监控脚本部署
- vite框架 ssr模型下 设置import.meta.env.MODE参数
- mysqldump的详细使用教程,定时备份脚本
- docker搭建maven私库Nexus3
- nSum的java解法
- QKCP容器平台安装qkcp &paas deployment
- Spring框架XML配置文件中的<bean>标签的作用