哈希应用之位图+布隆过滤器

bitset介绍

在 C++ 中，std::bitset 是一个标准库提供的类模板，用于表示固定大小的位集合。std::bitset 类模板允许你以一种方便且高效的方式处理位（二进制位）的集合。它在编译时指定了位集合的大小，并提供了一系列位操作函数，如设置位、清除位、翻转位等。每个位都被映射为一个布尔值，可以被访问和操作。std::bitset 的大小是固定的，由模板参数决定。你需要在创建 std::bitset 对象时指定位集合的大小。例如std::bitset<8>表示一个 8 位的位集合，其中每个位都可以被设置为 0 或 1。std::bitset 提供了方便的接口来进行位级别的操作，例如将多个位集合按位与、按位或、按位取反等。此外，它还提供了一些成员函数来查询位集合的状态和属性，例如测试某个位是否被设置、计算位集合中置位（值为 1 的位）的个数等。

bitset的大小在编译时就需要确定

1. #include<bitset<bitste>>

2.std::bitset<4> foo(5);//用整数初始化  5二进制位：101  foo值：0101 当整数的大小超过位数时，从整数二进制的低位开始赋值，高位被舍弃

3.std::bitset<4> foo;//创建一个4位的位集，每一位默认为0，当整数的大小小于位数时，高位填充为0

4.std::bitset<4> foo(19);//用整数初始化，19二进制位：10011     foo值：0011
5.std::bitset<4> foo(std::string("0101")); //字符串初始化，字符串中必须只能含有‘0’/‘1’

在进行有参构造时，若参数的二进制表示比bitset的size小，则在前面用０补充(如上面的栗子)；

若比bitsize大，参数为整数时取后面部分，参数为字符串时取前面部分(比如下面这个李子)：

1. #include<bitset<bitste>>

2.bitset<2> bitset1(12);　　//12的二进制为1100（长度为４），但bitset1的size=2，只取后面部分，即00

3.string s = "100101";　　
  bitset<4> bitset2(s);　　//s的size=6，而bitset的size=4，只取前面部分，即1001

4. char s2[] = "11101";
   bitset<4> bitset3(s2);　　//与bitset2同理，只取前面部分，即1110

cout << bitset1 << endl;　　//00
cout << bitset2 << endl;　　//1001
cout << bitset3 << endl;　　//1110

bitset常用函数

位运算都可以用： 与、或、非、异或，左移，右移
foo&foo2
    
foo|foo2
    
~foo
    
foo^foo2
    
foo<<=2
    
foo>>=2
    
foo.size()      返回大小（位数）
foo.count()     返回1的个数
foo.any()       返回是否有1
foo.none()      返回是否没有1
foo.set()       全都变成1
foo.set(p)      将第p + 1位变成1
foo.set(p, x)   将第p + 1位变成x
foo.reset()     全都变成0
foo.reset(p)    将第p + 1位变成0
foo.flip()      全都取反
foo.flip(p)     将第p + 1位取反
foo.to_ulong()  返回它转换为unsigned long的结果，如果超出范围则报错
foo.to_ullong() 返回它转换为unsigned long long的结果，如果超出范围则报错
foo.to_string() 返回它转换为string的结果

	bitset<8> foo ("10011011");

    cout << foo.count() << endl;　　//5　　（count函数用来求bitset中1的位数，foo中共有５个１
    cout << foo.size() << endl;　　 //8　　（size函数用来求bitset的大小，一共有８位

    cout << foo.test(0) << endl;　　//true　　（test函数用来查下标处的元素是０还是１，并返回false或true，此处foo[0]为１，返回true
    cout << foo.test(2) << endl;　　//false　　（同理，foo[2]为０，返回false

    cout << foo.any() << endl;　　//true　　（any函数检查bitset中是否有１
    cout << foo.none() << endl;　　//false　　（none函数检查bitset中是否没有１
    cout << foo.all() << endl;　　//false　　（all函数检查bitset中是全部为１

位图的简单实现

数据是否在给定的整型数据中，结果是在或者不在，刚好是两种状态，那么可以使用一
个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0
代表不存在。

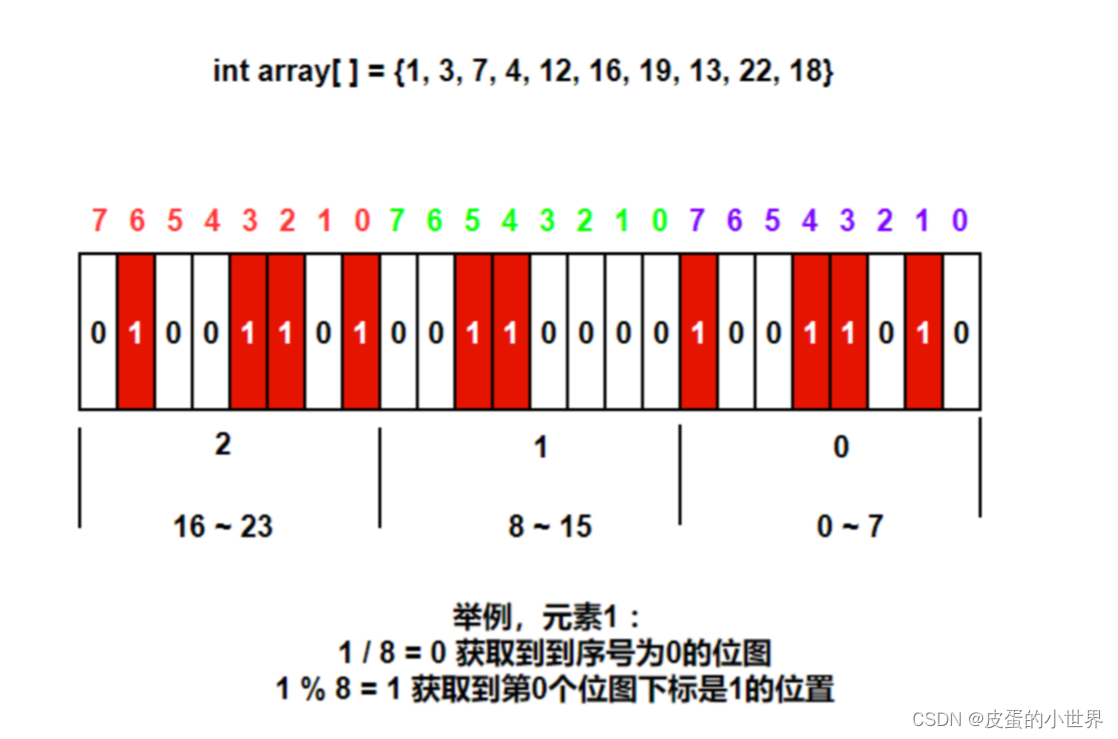
bitset能实现对数字的位的操作，同时也能通过类似于数组的下标来访问各个位的数值，以执行相应的操作。模拟bitset就是用一个普通的数组来存储数据以达到模拟的目的。

如果我们以一个整型作为比特位的容器，那么如果要求0~N范围的比特位，就需要有N/32+1 个整型来容纳这些比特位，同理如果以char为容器，则需要N/8+1个char来容纳N个比特位。这里我们用vector数组作为底层容纳比特位的容器，且其存储的数据类型为int。

#pragma once
#include <iostream>
#include <string>
#include <vector>
#include <bitset>

using namespace std;

namespace zxy
{
	template<size_t N>   //N表示需要几个比特位
	class bitset
	{
	public:
		bitset()
		{
			_bs.resize(N % 32 + 1, 0);  //计算当前需要几个int + 1
		}
		void set(size_t x)
		{
			size_t i = x / 32;  //计算当前的x在第几个整型
			size_t j = x % 32;  //计算在这个整型的第几个位置上
			//将对应的第i个整型的第j为改成1
			_bs[i] |= (1 << j);
		}

		void reset(size_t x)
		{
			size_t i = x / 32;  //计算当前的x在第几个整型
			size_t j = x % 32;  //计算在这个整型的第几个位置上
			//将对应的第i个整型的第j为改成0
			_bs[i] &= ~(1 << j);
		}

		bool test(size_t x)
		{
			//检测当前x代表的那一bit位是否是1 / 0
			size_t i = x / 32;  //计算当前的x在第几个整型
			size_t j = x % 32;  //计算在这个整型的第几个位置上
			return _bs[i] & (1 << j);
		}
	private:
		vector<int> _bs;
	};
}

布隆过滤器

位图有使用起来，节省空间，并且效率高的优点。位图的缺点，只能处理整形。
假如起昵称时要看一个字符串有没有被占用，用一个bit位标识。哈希解决冲突时，可以把后续同样位置冲突的元素的挂起来，形成链表。但是现在，如果要用位图存储字符串，bit位存不了指针，挂不起来，处理不了哈希冲突。如果用哈希存储又会浪费空间。
因此能不能考虑将哈希和位图结合针对字符串等非整形的类型，设计一个像位图一样的判断key在不在的节省空间的数据结构呢？可以——布隆过滤器
布隆过滤器是一种紧凑的、巧妙的概率型数据结构，能够高效插入查询，来判断一个元素在或不在，用多个哈希函数，把一个数据映射到位图中，不仅能提高查询效率，还能节省空间

布隆过滤器实现

成员只需要一个位图即可

//N表示需要多少比特位
template<size_t N, class K = string,
	     class HashFunc1 = HashBKDR, 
		 class HashFunc2 = HashAP,  
		 class HashFunc3 = HashDJB>
class BloomFilter
{
public:
	void Set(const K& key)
	{
		//计算key对应的数字
		size_t hash1 = HashFunc1()(key) % N;
		size_t hash2 = HashFunc2()(key) % N;
		size_t hash3 = HashFunc3()(key) % N;
		//将key在位图上对应的位置找到进行置1
		_bs.set(hash1);
		_bs.set(hash2);
		_bs.set(hash3);

		//cout << hash1 << " " << hash2 << " " << hash3 << " " << endl;
	}

	bool Test(const K& key)
	{
		size_t hash1 = HashFunc1()(key) % N;
		//检查当前key不在，一定正确
		if (_bs.test(hash1) == false)
			return false;
		size_t hash2 = HashFunc2()(key) % N;
		if (_bs.test(hash2) == false)
			return false; 
		size_t hash3 = HashFunc3()(key) % N;
		if (_bs.test(hash3) == false)
			return false;
		//说明三个值都在，不一定正确，可能有误判情况
		return true;
	}
private:
	bitset<N> _bs;
};

三种哈希函数
由于要用三种不同的哈希算法进行计算来降低冲突，因此，可以选择3种不同的哈希算法：
BKDR

struct HashBKDR
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (auto e : s)
		{
			value += e;
			value *= 131;
		}
 
		return value;
	}
};

AP

struct HashAP
{
	size_t operator()(const string& s)
	{
		register size_t hash = 0;
		size_t ch;
		for (long i = 0; i < s.size(); i++)
		{
			ch = s[i];
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
			}
			else
			{
				hash ^= (~(hash << 11) ^ ch ^ (hash >> 5));
			}
		}
 
		return hash;
	}
};

DJB

struct HashDJB
{
	size_t operator()(const string& s)
	{
		register size_t hash = 5381;
		for (auto e : s)
		{
			hash += (hash << 5) + e;
		}
 
		return hash;
	}
};

删除
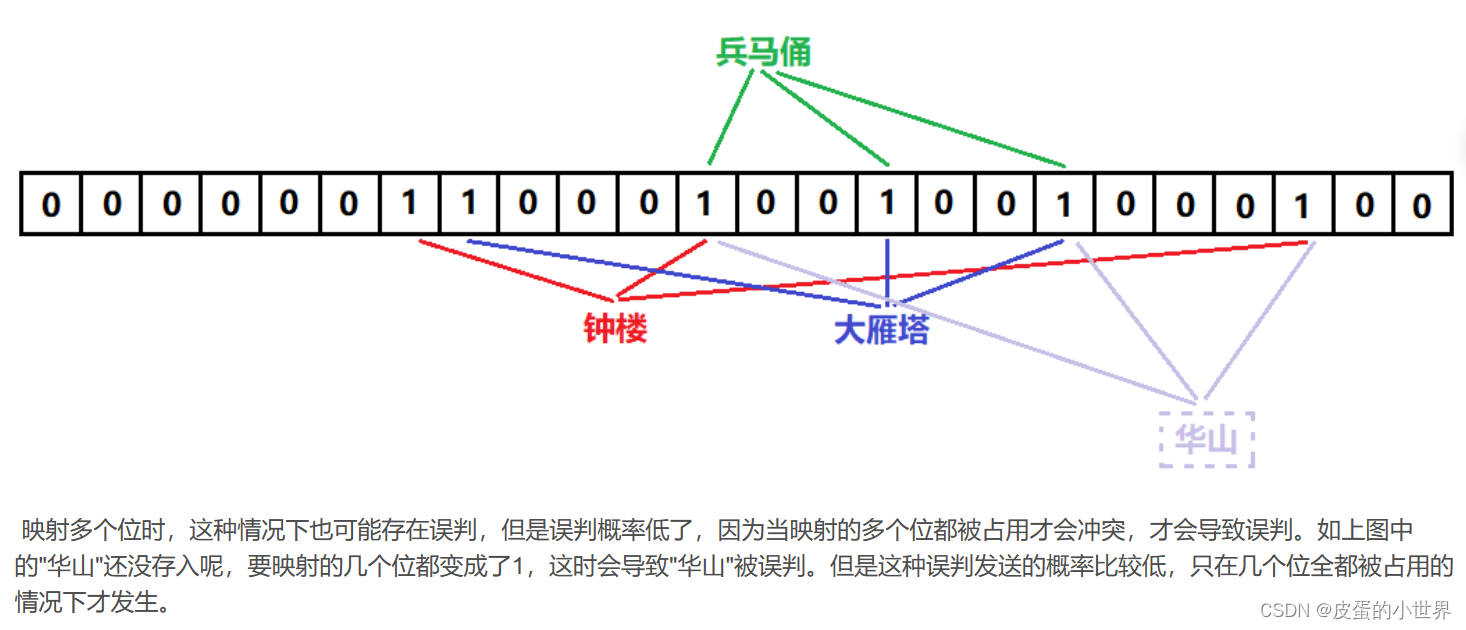
布隆过滤器不能直接支持删除工作，因为在删除一个元素时，可能会影响其他元素

比如：删除"钟楼"元素，如果直接将该元素所对应的二进制比特位置0，“华山”元素也被删除了，因为这两个元素在多个哈希函数计算出的比特位上刚好有重叠。