K-means聚类

1.Supervised vs. Unsupervised learning（监督学习与无监督学习）

1.1 Supervised learning

• 训练数据包括输入数据和相应的标签或目标输出

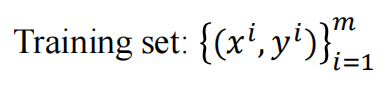
• 使用模型预测与实际标签之间的误差来学习模型参数
• 目标是建立一个从输入到输出的映射，使得模型能够根据输入数据准确地预测或分类输出结果

????????常见的监督学习任务包括分类（Classification）和回归（Regression）任务。在分类任务中，模型根据输入将其分为不同的类别；在回归任务中，模型预测连续值输出。

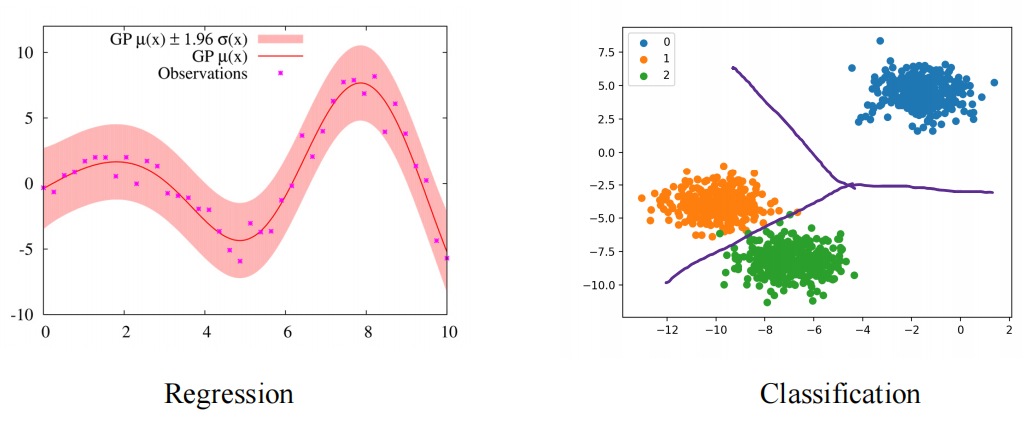
? ? ? ? 属于监督学习的算法包括线性回归、逻辑回归、感知机、SVM、神经网络等等

1.2 unsupervised learning

• 无监督学习算法从未标记或没有目标输出的数据中学习。

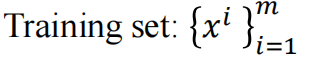
• 这类算法试图找到数据中的模式、结构或特征，以便对数据进行更好的理解、表示或组织。

????????常见的无监督学习任务包括聚类（Clustering）、降维（Dimensionality Reduction）、关联规则学习（Association Rule Learning）等。在聚类任务中，算法尝试根据数据的相似性将其分成不同的组；在降维任务中，算法试图减少数据的维度，保留最重要的特征信息。

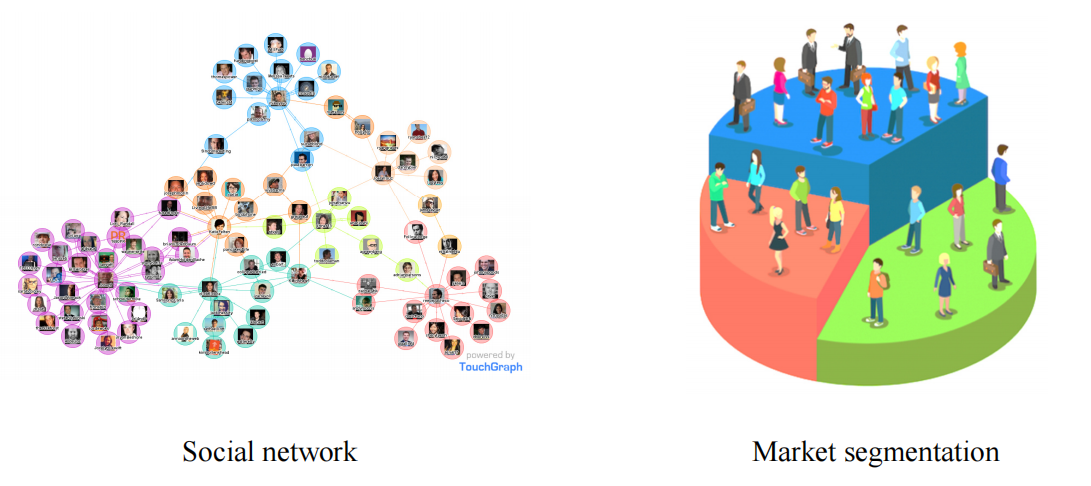
属于无监督学习的算法包括

? K-means（使用单个质心向量表示一个簇）

? 高斯混合模型（GMMs）（使用高斯概率密度函数表示一个簇）

? 变分推断（无需预先确定簇的数量）

1.3 self-supervised learning——自监督学习

????????自监督学习是一种无需人工标注标签或者外部监督的学习方式。它通过使用数据本身的特征来生成标签或者辅助任务，从而让模型在学习过程中自我监督。

????????在自监督学习中，模型会从数据中学习，但不是直接使用人工标注的标签。相反，它利用数据内在的结构、特性或者进行某些变换，在这些变换后的数据中提取信息作为“伪标签”或者作为辅助任务的目标。模型随后尝试优化自身以最大化预测这些伪标签或者辅助任务目标的准确性。

例如：

? 使用部分观察数据来预测其他部分（图像恢复，修补）

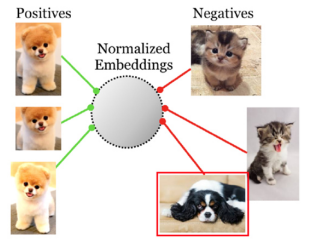
? 使用对比学习来学习语义

2. K-means

1.K-means流程

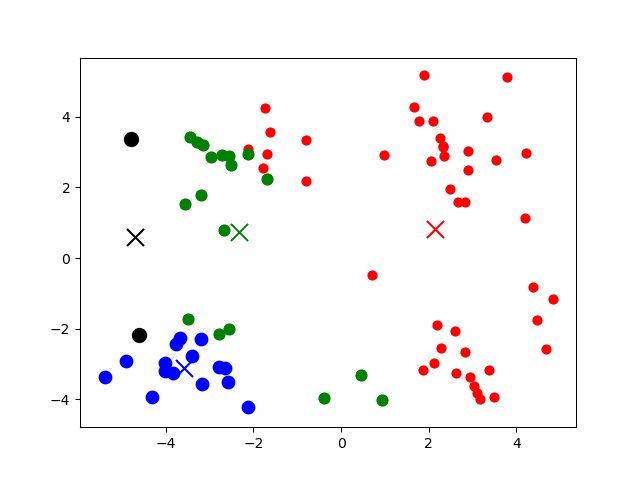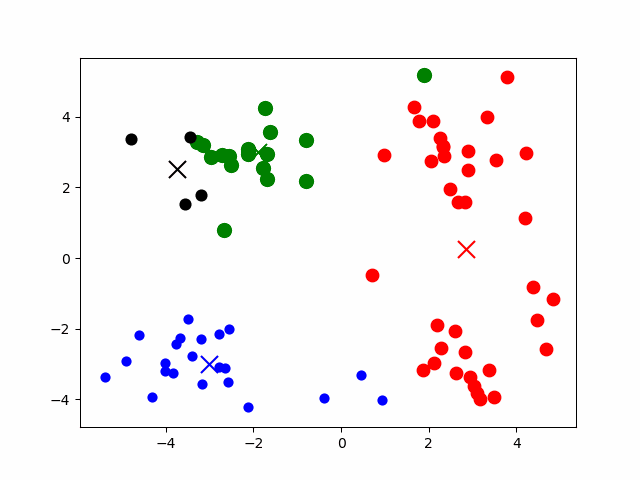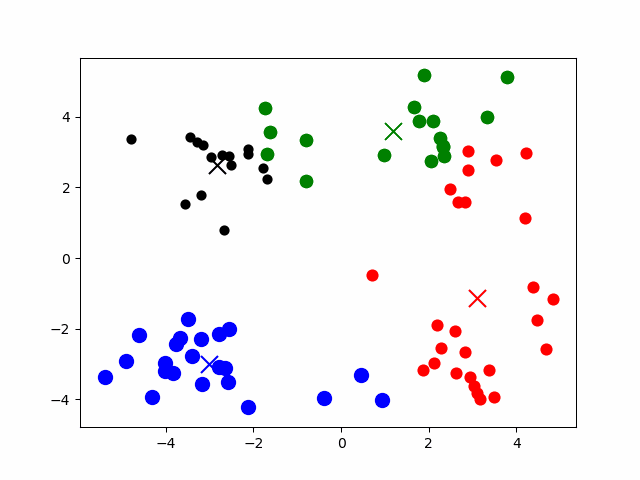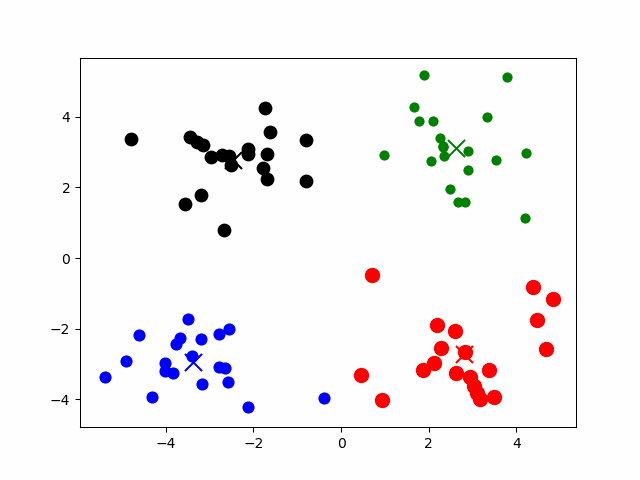
? ? ? ? K-means属于无监督学习的聚类算法。输入一个未标记的数据集，然后将数据集聚类成不同的组。

? ? ? ? K-means是一个迭代算法，假设我们想要将数据聚类成K个簇

1. 首先选择K个随机的点，作为聚类中心（clustercentroids）
2. 对于数据集中的每一个数据，按照距离K个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类
3. 计算每一个组的平均值，将该组所关联的聚类中心移动到平均值的位置成为新的聚类中心
4. 重复步骤2-3直至中心点不再变化

2.损失函数

? ? ? ? ?K-means的目标使最小化所有的数据点与其所关联的聚类中心点之间的平均距离。因此K-means的损失函数为畸变函数（distortion function）

• 表示数据点目前被分配的聚类中心的索引（从 1 到 K）
• 表示第k个聚类中心
• 表示第i个数据点所属的聚类中心

????????

3.随机初始化

????????在运行K-均值算法之前我们首先要随机初始化所有的聚类中心点，

1.首先应该选择K<m，即聚类中心点的个数要小于所有训练集实例的数量

2.随机选择K个训练实例，然后令K个聚类中心分别与这K个训练实例相等

????????????????????????????????????????????????????????????????????????????

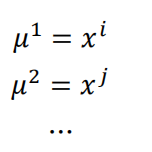
Local optima（局部最小值）

????????不同的初始化情况可能会导致最终生成不同的簇

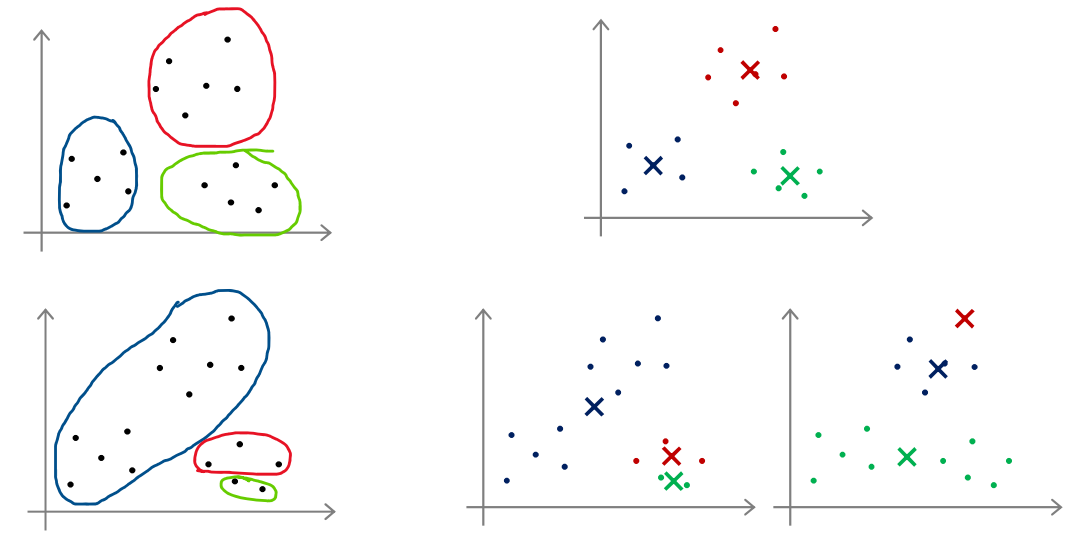
????????为了解决这个问题，我们通常需要多次运行K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值的结果，选择损失函数最小的结果。

? ? ? ? 但这种方法在K较小的时候（2--10）还是可行的，但是如果K较大，这么做也可能不会有明显地改善。

4.怎么选择合理K值

1.肘部法则

????????

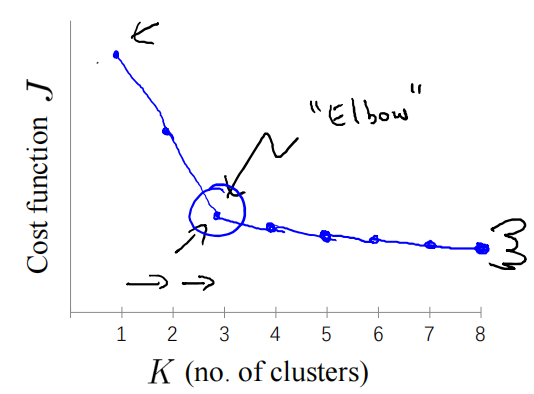
? ? ? ? 当我们使用不同的K值可以绘制出K值关于损失函数的图像，好像人的手臂，如果你伸出你的胳膊，那么这就是你的肩关节、肘关节、手，这就是“肘部法则”。从1到2，从2到3畸变值会迅速下降，在3的时候达到一个肘点，在此之后，畸变值就下降的非常慢，那么可以就选择K=3

2.人工选择

? ? ? ? 更多的时候需要根据我们实际的任务情况及所要实现的目的来选择K值。

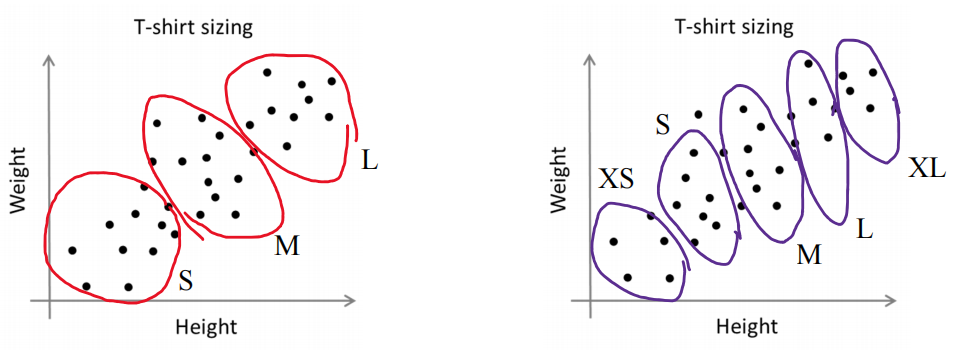
? ? ? ? 例如T-恤制造的例子，我们要将用户按照身材聚类，我们可以分成3个尺寸：S，M，L，也可以分成5个尺寸XS，S，M，L，XL，这样的选择是建立在回答"聚类后我们制造的T-恤是否能较好地适合我们的客户”这个问题的基础上作出的。

3.Gaussian Mixture Models (GMMs)——高斯混合模型

GMMs 假设数据是从多个高斯分布中抽样得到的，每个高斯分布称为一个“组件”。这些组件具有各自的均值和方差，它们可以具有不同的权重来表示它们在整体数据分布中的贡献程度。

在 GMMs 中，通常有两个阶段：

1. E步骤（Expectation Step）：

   • 在这一步中，首先假设每个数据点是从每个高斯分布中抽样得到的，计算每个数据点属于每个高斯分布的概率（即后验概率）。
   • 根据每个数据点与各个高斯分布的后验概率来更新数据点的分配情况。

2. M步骤（Maximization Step）：

   • 在这一步中，使用期望步骤中计算得到的数据点分配情况，重新估计每个高斯分布的参数（均值和方差）以及各个高斯分布的权重。
   • 这一步旨在最大化似然函数，即使模型更好地拟合数据。

重复进行期望步骤和最大化步骤，直到模型收敛或达到预定的迭代次数。最终，GMMs 能够提供对数据的聚类信息，即哪些数据点更有可能属于哪个高斯分布组件。

? 优点：

???????? ? 使用高斯概率密度函数而不是质心向量来表示簇 ? 能够提供更多关于簇的信息

? 缺点：

???????? ? 仍然需要预先确定簇（组件）的数量

4.Variational Inference——变分推断??

? 思路：

????????? 使用一个易处理的概率密度函数来近似数据的后验分布。后验概率指的是观察数据属于某一类的概率。

? 优点：

????????? 它可以自动发现数据中的聚类数量

? 缺点：

???????? ? 优化可能需要很长时间才能收敛。

?