图神经网络与分子表征：6. EGNN

很多人在完成升学考试后便很少参与公式推导这种数学锻炼，导致大家对数学公式避之不及。事实上，很多经典的神经网络框架正是基于简单、直观的数学推导搭建的。本文将要介绍的 EGNN (2021 ICML) 正是其中之一。

前言

EGNN 的诸多作者中并没有长期从事 AI for Science 的研究员。第一通讯 Max Welling 是被引 10w+ 的传统 AI 领域大牛，第一作者 Victor Garcia Satorras 在发完这篇后，似乎没再发过有影响力的作品。倒是第二作者 Emiel Hoogeboom 在这篇论文后发布了鼎鼎大名的 EDM 。由于 EDM 中使用的表征模型正是 EGNN，所以 EGNN 被计算机领域的各路大神奉为圭臬，尤其是各种各样的扩散生成模型，其表征框架一般都是 EGNN。因此说，EGNN 是当下扩散模型的宠儿一点不为过。
在阅读 EGNN 论文时，能明显感觉到作者是行外玩家，行文逻辑中看不到一点化学、物理含义，就是拼凑各种网红关键词的裁缝作品。比如，作者说自己的网络是一个等变网络，就在标题里大大方方写上 Equivariant 。各种引文在引用这篇文章时也不分青红皂白，直接说这是一个等变网络。这里想吐槽下，传统 AI 会议论文有时候真的就是直白、逻辑简单。因为 AI 发展到今天更像是一个搭积木的游戏。很多行外人其实并不关心积木本身是怎么样的，他们大多只是听到一些关键词，比如，等变，等变的好，我就找一个等变的模型，大家都用 EGNN，我也用 EGNN，没了。
OK，闲话少说，咱们进入正题

公式化

使用数学公式清晰、准确的描述先有框架是理性设计新模型的基础。在 EGNN 中，作者首先对 GNN 进行了公式化描述：

作者将图神经网络的工作流程划分成了三段：

1. 消息制备：对应图神经网络里的边，消息的制备是由两点距离 aij，周边邻居 j 的隐变量和节点 i 本身的隐变量完成的，外边套一个神经网络 ${?}_e$ ，增加拟合能力。
2. 消息聚合：一般的 GNN 都是将邻居的消息进行相加。
3. 隐变量迭代：在完成消息制备和聚合后，我们需要对所有节点的隐变量进行迭代

作者随后对常见神经网络进行公式化，例如，Schnet 如下：

我们对应下之前的解析：

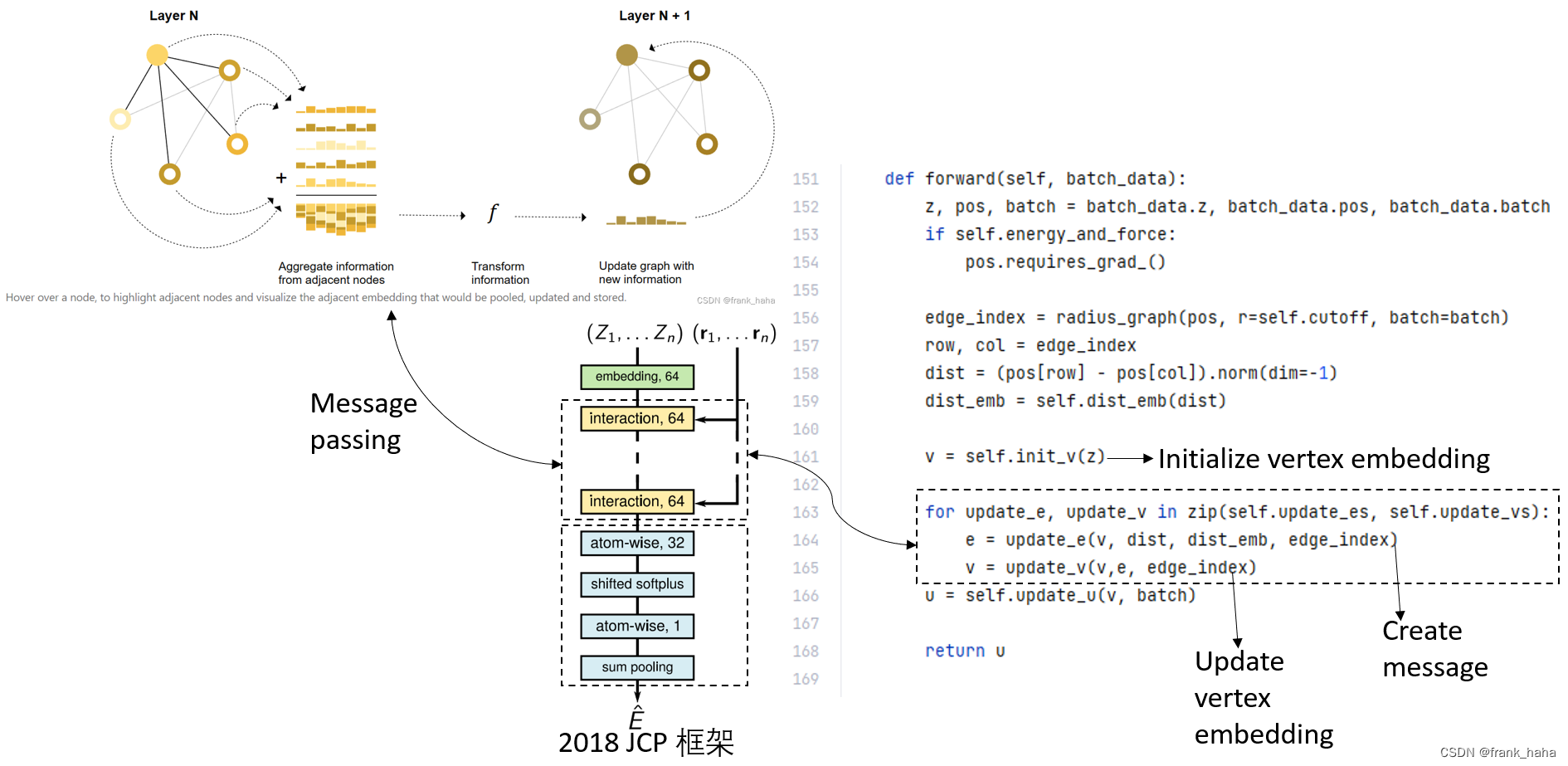
可以看到，schnet 框架被精准解析，该框架在后两步消息聚合和隐变量迭代跟传统 GNN 并无区别，只是在第一步制备消息时加了一个平滑的激活函数${?}_{cf}$。

EGNN 公式推导

在对前人工作进行总结之后，EGNN 作者们变开始着手设计等变网络，其设计思路可谓是简单粗暴。
首先，等变是什么？可以参考前一篇文章
简单来说，当分子的输入坐标进行旋转时，分子中原子受力等性质也会随着坐标的旋转而旋转。
那么，为什么之前那么多模型不是等变的呢？
作者指出，之前的模型只用了原子间距离，这是一个标量啊，不会随分子旋转而发生变化。
那怎么把距离信息转化成有方向的矢量呢？作者提出了和 PAINN 同样的思路：使用向量。
但是实操起来，非常简单粗暴，直接把原子坐标信息加到了神经网络的迭代过程中。说实话，看到这里呆住了。不愧是计算机大佬。没那么多弯弯绕。读过我的 PAINN解析 的朋友可能还记得，PAINN 讲了一个非常物理、有深度的故事，一步步将向量引入进来。EGNN 的行文逻辑太简单了：

• 之前的网络不等变，是因为与坐标相关的信息在提取完原子间距离后直接扔了。这样旋转坐标就无法影响到 target 的方向。
• 那我直接把坐标加到消息传递的每一步不就好了。
• 作者扔出了一堆公式：
  
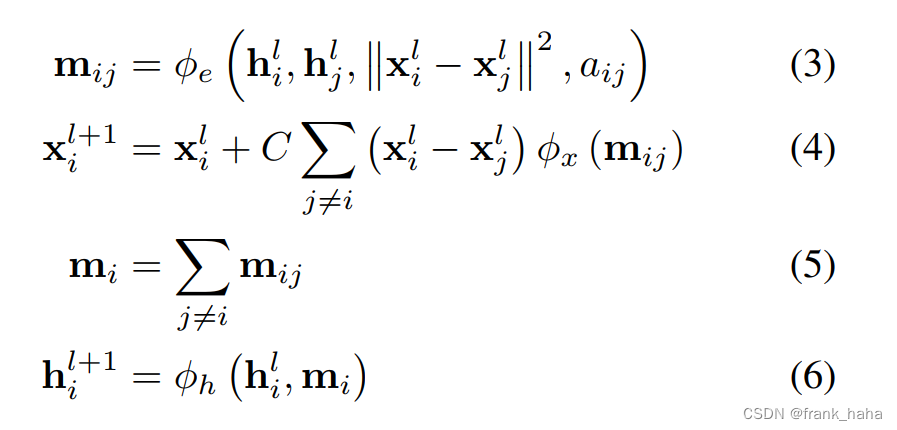
  与上面经典 GNN 相比，消息聚合和节点隐变量迭代维持不变，唯一有所区别的是消息制备过程。公式 (3) 和 Schnet 的框架基本一致，也是提取两原子间的标量距离信息。只不过这里的原子坐标替换成了会变的原子坐标。公式 (4) 指出，原子坐标怎么变比较合适。公式 (4) 可谓是全文的精髓，通过显式的更迭原子坐标，作者实现了迭代后的坐标相对输入坐标的等边性。但也仅此而已。与节点隐变量迭代相关的公式 (3) (5) (6) 均是不变网络。如果整个网络在做下游任务时只用节点隐变量，整个网络还是不变网络。如果能像 PAINN 那样将等变的向量和不变的节点信息进行混合，再进行下游任务，此时将是一个等变网络。这一点，EGNN 的作者一笔带过，只是在最后的附录里给出了证明过程，并承认，节点隐变量是一个不变网络。
  下面我将尝试顺着 EGNN 原文的思路对 EGNN 的等变性进行推导：

1. 证明对象：
   
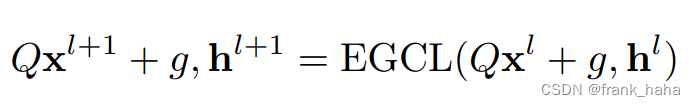
   作者首先明确了证明对象。GNN 是由多个消息传递层叠加得到的。EGNN 同样也是，作者将每个消息传递层叫做 EGCL (equivariant graph convolutional layer)。坐标旋转对性质预测的影响可以拆分成，经过每一层时的影响，每一层都等变了，整体就是等变的。
   等式右边表示，输入坐标进行旋转。等式坐标表示，输出的坐标也会随之旋转。这就是等变的标准描述。注意，节点隐变量 $h^{l+1}$ 并没有随输入坐标变化。因此，节点隐变量是一个不变量。
2. 逐个击破
   作者引入了四个公式，只要我们挨个证实每个公式都不会对最终的，坐标 $x^{l+1}$ 造成影响即可。
   
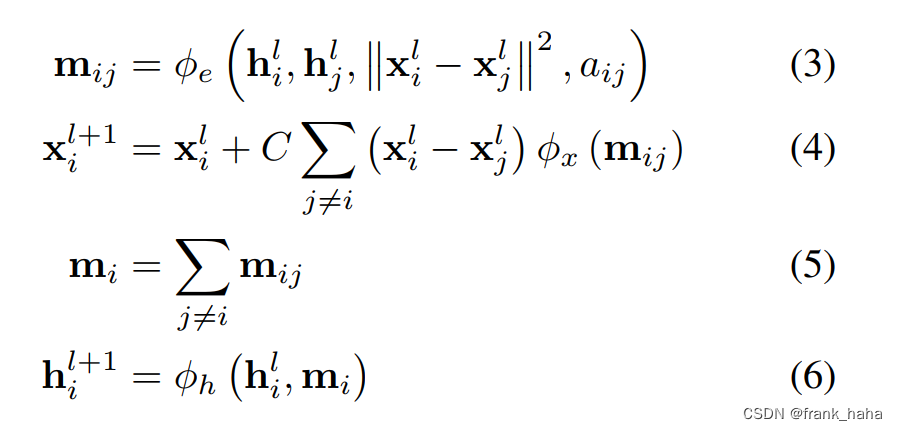
   对于公式 3，作者证明，坐标旋转不会对等变性造成影响：
   
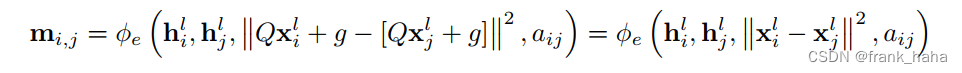
   因此 $m_{i,j}$ 是一个不变量。注意到，公式 5,6 在对节点隐变量进行迭代时，仅使用了 $m_{i,j}$，所以，节点隐变量是一个不变量。
   下面，作者证明，原子坐标在迭代过程中将维持等变性：
   
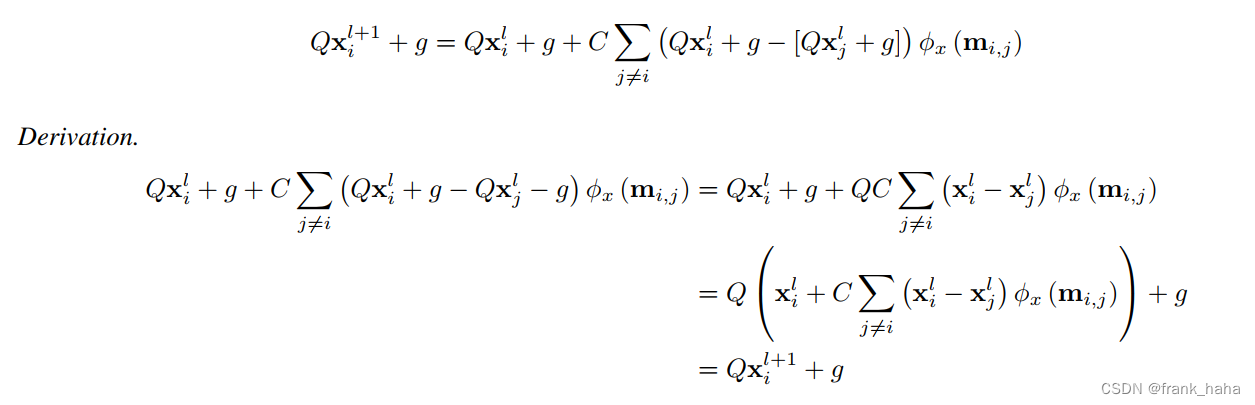
   这里的证明过程简单直白，就是将公式 4 中的坐标替换成经过旋转后的坐标，再进行简单展开合并即可。
   至此，作者证明完毕。
   值得一提的是，大部分神经网络在使用时仅有效利用节点隐变量，而这一点在 EGNN 中被忽略。EGNN 的节点隐变量是一个不变量，但是大部分使用者不会关心这些细节，他们只是将 EGNN 作为自己的一块积木，说是等变的模型就是等变的。所以大家在使用 EGNN 时需要多加小心。
   在阅读 EGNN 论文的时候，我时常会想起 PAINN。两者架构何其相似，但 PAINN 的行文逻辑物理的多，最后还教大家如何有效利用 vector 信息。
   这篇文章就介绍到这里，谢谢大家。