代码随想录刷题题Day32

刷题的第三十二天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day32 任务
● 70. 爬楼梯 （进阶）
● 322. 零钱兑换
● 279.完全平方数

1 爬楼梯（进阶）

70. 爬楼梯 （进阶）

思路：
动态规划
（1）确定dp数组以及下标的含义
dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法。
（2）确定递推公式
$dp[i]+=dp[i?j];$
（3）dp数组如何初始化

vector<int> dp(n + 1, 0);
dp[0] = 1;

（4）确定遍历顺序
背包里求排列问题，需要将背包放在外面，物品放在里面。
（5）举例来推导dp数组

C++：

#include <iostream>
#include <vector>
using namespace std;
int main()
{
    int m,n;
    cin >> n >> m;
    vector<int> dp(n + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= n; i++) { // 遍历背包
        for (int j = 1; j <= m; j++) { // 遍历物品
            if (i - j >= 0) dp[i] += dp[i - j];
        }
    }
    cout << dp[n] << endl;
}

时间复杂度: $O(n?m)$
空间复杂度: $O(n)$

2 零钱兑换

322. 零钱兑换

思路：
动态规划
（1）确定dp数组以及下标的含义
dp[j]：凑足总额j所需钱币的最少个数
（2）递推公式
$dp[j]=min(dp[j?coins[i]]+1,dp[j]);$
（3）dp数组如何初始化

vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;

（4）确定遍历顺序
求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。

1. 如果求组合数就是外层for循环遍历物品，内层for遍历背包。
2. 如果求排列数就是外层for遍历背包，内层for循环遍历物品。

（5）举例推导dp数组

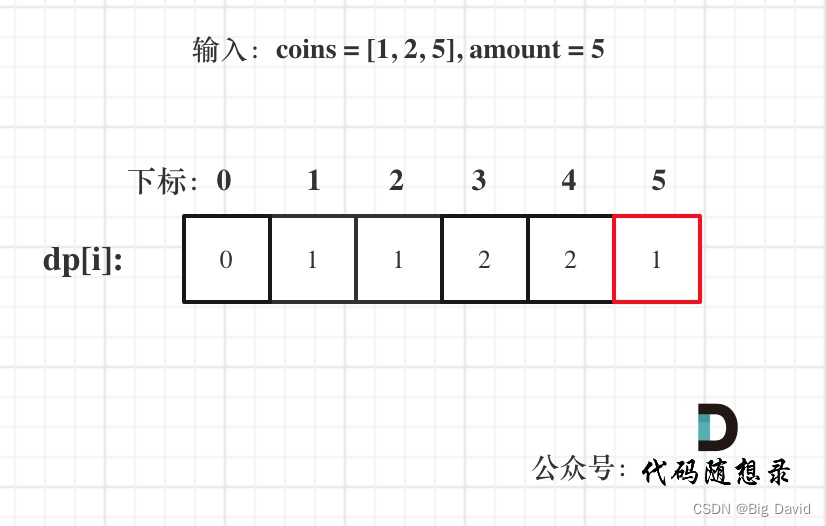
C++：

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, INT_MAX);
        dp[0] = 0;
        for (int i = 0; i < coins.size(); i++) {// 遍历物品
            for (int j = coins[i]; j <= amount; j++) {// 遍历背包
                if (dp[j - coins[i]] != INT_MAX) // 如果dp[j - coins[i]]是初始值则跳过
                	dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
            }
        }
        if (dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

时间复杂度: $O(n?amount)$，其中 n 为 coins 的长度
空间复杂度: $O(amount)$

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, INT_MAX);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {// 遍历背包
            for (int j = 0; j < coins.size(); j++) {// 遍历物品
                if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX) dp[i] = min(dp[i - coins[j]] + 1, dp[i]);
            }
        }
        if (dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

3 完全平方数

279.完全平方数

思路：
动态规划
（1）确定dp数组（dp table）以及下标的含义
dp[j]：和为j的完全平方数的最少数量
（2）确定递推公式
$dp[j]=min(dp[j?i?i]+1,dp[j]);$
（3）dp数组如何初始化

vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;

（4）确定遍历顺序

本题外层for遍历背包，内层for遍历物品，还是外层for遍历物品，内层for遍历背包，都是可以的

（5）举例推导dp数组

C++：

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n + 1, INT_MAX);
        dp[0] = 0;
        for (int i = 1; i * i <= n; i++) {// 遍历物品
            for (int j = i * i; j <= n; j++) {// 遍历背包
                dp[j] = min(dp[j], dp[j - i * i] + 1);
            }
        }
        return dp[n];
    }
};

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n + 1, INT_MAX);
        dp[0] = 0;
        for (int i = 1; i <= n; i++) {// 遍历背包
            for (int j = 1; j * j <= i; j++) {// 遍历物品
                dp[i] = min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }
};

时间复杂度: $O(n?\surd n)$
空间复杂度: $O(n)$

---

鼓励坚持三十三天的自己😀😀😀