《剑指offer》 图专项突破

第十五章：图

面试题105：最大的岛屿

题目

海洋岛屿地图可以用由0、1组成的二维数组表示，水平或者竖直方向相连的一组1表示一个岛屿。请计算最大的岛屿的面积（即岛屿中1的数目）。例如，在图15.5中有4个岛屿，其中最大的岛屿的面积为5。

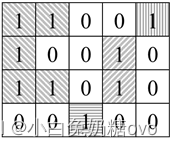
图15.5：用0、1矩阵表示的海洋岛屿地图。地图中有4个岛屿，最大的岛屿的面积为5。

参考代码

解法一

public int maxAreaOfIsland(int[][] grid) {
   
    int rows = grid.length;
    int cols = grid[0].length;
    boolean[][] visited = new boolean[rows][cols];
    int maxArea = 0;
    for (int i = 0; i < rows; i++) {
   
        for (int j = 0; j < cols; j++) {
   
            if (grid[i][j] == 1 && !visited[i][j]) {
   
                int area = getArea(grid, visited, i, j);
                maxArea = Math.max(maxArea, area);
            }
        }
    }

    return maxArea;
}

private int getArea(int[][]grid, boolean[][] visited, int i, int j) {
   
    Queue<int[]> queue = new LinkedList<>();
    queue.add(new int[]{
   i, j});
    visited[i][j] = true;

    int[][] dirs = {
   {
   -1, 0}, {
   1, 0}, {
   0, -1}, {
   0, 1}};
    int area = 0;
    while (!queue.isEmpty()) {
   
        int[] pos = queue.remove();
        area++;

        for (int[] dir : dirs) {
   
            int r = pos[0] + dir[0];
            int c = pos[1] + dir[1];
            if (r >= 0 && r < grid.length
                && c >= 0 && c < grid[0].length
                && grid[r][c] == 1 && !visited[r][c]) {
   
                queue.add(new int[]{
   r, c});
                visited[r][c] = true;
            }
        }
    }

    return area;
}

解法二

public int maxAreaOfIsland(int[][] grid) {
   
    int rows = grid.length;
    int cols = grid[0].length;
    boolean[][] visited = new boolean[rows][cols];
    int maxArea = 0;
    for (int i = 0; i < rows; i++) {
   
        for (int j = 0; j < cols; j++) {
   
            if (grid[i][j] == 1 && !visited[i][j]) {
   
                int area = getArea(grid, visited, i, j);
                maxArea = Math.max(maxArea, area);
            }
        }
    }

    return maxArea;
}

private int getArea(int[][]grid, boolean[][] visited, int i, int j) {
   
    Stack<int[]> stack = new Stack<>();
    stack.push(new int[]{
   i, j});
    visited[i][j] = true;

    int[][] dirs = {
   {
   -1, 0}, {
   1, 0}, {
   0, -1}, {
   0, 1}};
    int area = 0;
    while (!stack.isEmpty()) {
   
        int[] pos = stack.pop();
        area++;

        for (int[] dir : dirs) {
   
            int r = pos[0] + dir[0];
            int c = pos[1] + dir[1];
            if (r >= 0 && r < grid.length
                && c >= 0 && c < grid[0].length
                && grid[r][c] == 1 && !visited[r][c]) {
   
                stack.push(new int[]{
   r, c});
                visited[r][c] = true;
            }
        }
    }

    return area;
}

解法三

public int maxAreaOfIsland(int[][] grid) {
   
    int rows = grid.length;
    int cols = grid[0].length;
    boolean[][] visited = new boolean[rows][cols];
    int maxArea = 0;
    for (int i = 0; i < rows; i++) {
   
        for (int j = 0; j < cols; j++) {
   
            if (grid[i][j] == 1 && !visited[i][j]) {
   
                int area = getArea(grid, visited, i, j);
                maxArea = Math.max(maxArea, area);
            }
        }
    }

    return maxArea;
}

    private int getArea(int[][]grid, boolean[][] visited, int i, int j) {
   
        int area = 1;
        visited[i][j] = true;
        int[][] dirs = {
   {
   -1, 0}, {
   1, 0}, {
   0, -1}, {
   0, 1}};
        for (int[] dir : dirs) {
   
            int r = i + dir[0];
            int c = j + dir[1];
            if (r >= 0 && r < grid.length
                && c >= 0 && c < grid[0].length
                && grid[r][c] == 1 && !visited[r][c]) {
   
                area += getArea(grid, visited, r, c);
            }
        }
        
        return area;
    }

面试题106：二分图

题目

如果能将一个图的结点分成A、B两部分，使得任意一条边的一个结点属于A另一个结点属于B，那么该图就是一个二分图。输入一个由数组graph表示的图，graph[i]里包含所有和结点i相邻的结点，请判断该图是否为二分图。例如，如果输入graph为[[1, 3], [0, 2], [1, 3], [0, 2]]，那么我们可以将结点分为{0, 2}、{1, 3}两部分，因此该图是一个二分图，如图15.7（a）所示。如果输入graph为[[1,2,3],[0,2],[0,1,3],[0,2]]，则不是一个二分图，如图15.7（b）所示。

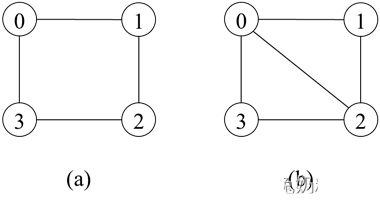
图15.7：二分图与非二分图。（a）二分图。（b）不是二分图。

参考代码

解法一

public boolean isBipartite(int[][] graph) {
   
    int size = graph.length;
    int[] colors = new int[size];
    Arrays.fill(colors, -1);
    for (int i = 0; i < size; ++i) {
   
        if (colors[i] == -1) {
   
            if (!setColor(graph, colors, i, 0)) {
   
                return false;
            }
        }
    }

    return true;
}

private boolean setColor(int[][] graph, int[] colors, int i, int color) {
   
    Queue<Integer> queue = new LinkedList<>();
    queue.add(i);
    colors[i] = color;
    while (!queue.isEmpty()) {
   
        int v = queue.remove();
        for (int neighbor : graph[v]) {
   
            if (colors[neighbor] >= 0) {
   
                if (colors[neighbor] == colors[v]) {
   
                    return false;
                }
            } else {
   
                queue.add(neighbor);
                colors[neighbor] = 1 - colors[v];
            }
        }
    }

    return true;
}

解法二

public boolean isBipartite(int[][] graph) {
   
    int size = graph.length;
    int[] colors = new int[size]