tamarin manual总结笔记4(使用规则的模型规范)
使用规则的模型规范
在本节中,我们现在提供底层模型的非正式描述。该模型的全部细节可以在(Schmidt 2012)中找到。
tamarin模型使用三个主要成分:
1.规则(Rules)
2.事实(Facts)
3.术语(Terms)
在前一节中,我们已经看到了术语的定义。在这里,我们将讨论事实和规则,并说明它们在Naxos协议中的用法,如下所示

在该协议中,每一方x都有一个长期私钥lkx和一个相应的公钥pkx = ‘g’^lkx,其中’g’是Diffie-Hellman组的生成器。因为g可以是公共的,所以我们把它当作一个公共常数来建模。这里使用了两个不同的哈希函数h1和h2。
要启动会话,发起者I首先创建一个新的临时eskI,也称为I的临时(私)密钥。然后,他将eskI与I的长期私钥lkI连接起来,使用哈希函数h1对结果进行哈希,并将’g’^h1(eskI,lkI)发送给响应器。响应者R将接收到的值存储在变量X中,根据自己的临时eskR和长期私钥lkR计算出类似的值,并将结果发送给发起者,发起者将接收到的值存储在变量Y中。最后,双方计算一个会话密钥(kI和kR),其计算包括他们自己的长期私钥,这样只有预期的合作伙伴才能计算相同的密钥。
注意,交换的消息没有经过身份验证,因为接收方无法验证在消息的构造中是否使用了预期的长期密钥。身份验证是隐式的,只有通过拥有正确的密钥才能保证。显式身份验证(例如,预期的合作伙伴最近还活着或同意某些值)通常在经过身份验证的密钥交换协议中通过添加密钥确认步骤来实现,其中双方交换交换消息的MAC,该消息是用计算的会话密钥(一种变体)进行密钥校验的。
规则
我们使用多集重写来指定协议的并发执行和对手。多集重写是一种通常用于并发系统建模的形式化方法,因为它自然地支持独立转换。
多集重写系统定义了一个转换系统,在我们的例子中,转换将被标记。系统的状态是事实的多集(包)。我们将在下面解释事实的类型及其用法。
Tamarin中的重写规则有一个名称和三个部分,每个部分都是一个事实序列:一个用于规则的左侧,一个用于标记转换(我们称之为“动作事实”),另一个用于规则的右侧。例如:
rule MyRule1:
[ ] --[ L('x') ]-> [ F('1','x'), F('2','y') ]
rule MyRule2:
[ F(u,v) ] --[ M(u,v) ]-> [ H(u), G('3',h(v)) ]
现在,我们将忽略动作事实(L(…)和M(…)),在下一节讨论属性时再回到它们。如果一个规则没有被动作事实标记,箭头符号—[]->可以缩写为—>。
规则名称仅用于引用特定的规则。它们没有特定的含义,可以任意选择,只要每个规则有一个唯一的名称即可。
执行
转换系统的初始状态是空多集。
规则定义了系统如何过渡到一个新状态。如果可以将规则实例化,使其左侧包含在当前状态中,则可以将规则应用于状态。在这种情况下,左边的事实从状态中移除,并被实例化的右边所取代。
例如,在初始状态下,MyRule1可以被重复实例化。
对于MyRule1的任何实例化,这会导致包含F(‘1’,‘x’)和F(‘2’,‘y’)的后续状态。MyRule2不能在初始状态下应用,因为它不包含F个事实。在后继状态下,规则MyRule2现在可以应用两次。它可以通过u = ‘1’ (v = ‘x’)或’2’ (v = ‘y’)来实例化。每个实例化都会导致一个新的后继状态。
在本地宏的规则中使用let绑定
在对更复杂的协议进行建模时,一个术语可能会在同一规则中多次出现(可能作为子术语)。为了使这些规范更具可读性,Tamarin提供了let…in,如下例所示:
rule MyRuleName:
let foo1 = h(bar)
foo2 = <'bars', foo1>
...
var5 = pk(~x)
in
[ ... ] --[ ... ]-> [ ... ]
这种let-binding表达式可用于在规则上下文中指定本地术语宏。
每个宏应该出现在单独的行上,并定义一个替换:=号的左边必须是一个变量,右边是一个任意项。将等式中出现的所有变量的右侧代入后,将解释该规则。如上例所示,宏可以使用先前定义的宏的左侧。
事实
事实符号F和项ti的形式为F(t1,…,tn)。它们有一个固定的密度(在本例中为n)。注意,如果一个Tamarin模型使用两个不同密度的相同事实,Tamarin将报告一个错误。
Tamarin有三种特殊的功能。它们被用来模拟与不可信网络的交互,并模拟唯一的新鲜(随机)值的生成。
In
这一事实用于模拟从由Dolev-Yao对手控制的不可信网络接收消息的一方,并且只能发生在重写规则的左侧。
Out
这一事实用于模拟向由Dolev-Yao对手控制的不可信网络发送消息的一方,并且只能发生在重写规则的右侧。
Fr
这个事实必须在生成新的(随机)值时使用,并且只能出现在重写规则的左侧,其参数是新项。Tamarin的底层执行模型具有用于生成Fr(x)事实实例的内置规则,并且还确保每个实例生成一个不同于所有其他的术语(实例化x)。
对于以上三个事实,Tamarin有自己的规则。特别是,有一个生成唯一的Fr(…)事实的新规则,以及一组用于对手知识派生的规则,这些规则消耗Out(…)事实并生成In(…)事实
线性事实与持久事实
上述事实被称为“线性事实”。它们不仅是由规则产生的,也可以被规则消耗。因此,它们可能出现在一种状态,而不是下一种状态。
相比之下,我们模型中的一些事实一旦被引入,就永远不会从状态中移除。
用线性事实来建模需要每个在左边有这样一个事实的规则,在右边也有这个事实的精确副本。虽然这种建模在理论上没有根本的问题,但它给用户带来了不便,而且还可能导致Tamarin探索与实践中跟踪这些事实无关的规则实例,这甚至可能导致不终止。
基于上述两个原因,我们现在引入“持久事实”,它永远不会从状态中移除。我们用“!”作为这些事实的前缀。
事实总是以大写字母开头,不需要明确声明。如果它们的名字前面有一个感叹号!,那么它们是持久的。否则,它们是线性的。注意,每个事实名称必须一致使用;也就是说,它必须始终以相同的密度、大小写、持久性和多样性来使用。除此之外,Tamarin抱怨说这个理论不够完善。
比较线性和持久事实行为,我们注意到,如果在某些规则的前提中存在一个持久事实,那么Tamarin将考虑在其结论中产生该持久事实的所有规则作为源。通常情况下,这样的规则很少(通常只有一条),这简化了推理。对于线性事实,特别是那些在许多规则中使用的事实(并且保持静态),显然有许多规则在其结论中包含事实(所有规则!)。因此,在任何前提下寻找源时,都需要考虑所有这些规则,这显然是效率较低且不容易终止的。因此,当尝试对从未使用过的事实建模时,首选使用持久事实。
嵌入式的限制
建模协议时经常使用的一个技巧是,一旦调用某个规则,就对跟踪实施限制,例如,如果规则表示的步骤在稍后的某个时间点需要另一个步骤,例如,为可靠通道建模。我们稍后会解释什么是限制,但粗略地说,它们指定了协议执行应该遵守的约束。
这可以手工完成,即通过指定一个指向该规则唯一的动作事实的限制,或者通过使用如下所示的嵌入式限制:
rule B:
[In(x), In(y)] --[ _restrict( formula )]-> []
公式是一个限制。请注意,嵌入式限制目前仅在跟踪模式下可用。
建模的协议
有几种方法可以定义安全协议的执行,例如(Cremers和Mauw 2012)。在Tamarin中,没有预定义的协议概念,用户可以根据自己的选择自由建模。下面我们给出一个如何对协议建模的示例,然后讨论替代方案。
公钥基础设施
在 Tamarin 模型中,没有预先定义的公钥基础设施(PKI)概念。可通过一条为一方生成密钥的规则来模拟一个预先分布的 PKI,该 PKI 的每一方都有非对称密钥。当事人的身份和公钥/私钥作为事实存储在状态中,以便协议规则检索。对于公钥,我们通常使用 Pk 事实,对于相应的长期私钥,我们使用 Ltk 事实。由于这些事实只会被其他规则用来检索密钥,而不会被更新,因此我们将它们建模为持久事实。我们使用抽象函数 pk(x) 来表示与私钥 x 相对应的公钥,从而得出以下规则。请注意,我们也直接将所有公钥交给攻击者,右侧的 Out 表示攻击者。
rule Generate_key_pair:
[ Fr(~x) ]
-->
[ !Pk($A,pk(~x))
, Out(pk(~x))
, !Ltk($A,~x)
]
一些协议,如Naxos,依赖于密钥对的代数特性。在许多基于DH的协议中,公钥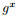 代表私钥x,这允许利用指数的可交换性来建立密钥。在这种情况下,我们指定以下规则。
代表私钥x,这允许利用指数的可交换性来建立密钥。在这种情况下,我们指定以下规则。
rule Generate_DH_key_pair:
[ Fr(~x) ]
-->
[ !Pk($A,'g'^~x)
, Out('g'^~x)
, !Ltk($A,~x)
]
模拟协议步骤
协议描述系统中代理的行为。代理可以执行协议步骤,例如接收消息并通过发送消息进行响应,或者启动会话。
对Naxos应答者角色进行建模
我们首先对响应者角色建模,它比发起者角色更简单,因为它可以在一个规则中完成。
该协议使用Diffie-Hellman求幂和两个哈希函数h1和h2,我们必须声明它们。我们可以用:
builtins: diffie-hellman
和
functions: h1/1
functions: h2/1
如果没有任何进一步的方程,以这种方式声明的函数将表现为单向函数。
代理 $R的响应线程每次接收到一条消息时,都会生成一个新的值~eskR,发送一条响应消息,并计算一个密钥kR。我们可以通过在规则左侧指定一个In事实来建模接收消息。为了对新值的生成建模,我们要求它由内置的fresh规则生成。
最后,该规则依赖于参与者的长期私钥,我们可以从前面介绍的Generate_DH_key_pair规则生成的持久事实中获得该私钥。
响应消息是g的计算哈希函数的幂的幂。由于哈希函数是一元的,如果我们想在两条消息的连接上调用它,我们将它们建模为一对<x,y>,这将用作h1的单个参数。
因此,这一规则的初步形式化可能如下:
rule NaxosR_attempt1:
[
In(X),//接收到X
Fr(~eskR),//生成新鲜随机数eskR
!Ltk($R, lkR)//持久事实,$R的长期私人密钥
]
-->
[
Out( 'g'^h1(< ~eskR, lkR >) )//向$I发送信息
]
然而,应答者也计算会话密钥kR,由于会话密钥不影响发送或接收的消息,我们可以从规则的左侧和右侧省略它。但是,稍后我们将希望在security属性中对会话密钥进行声明。因此,我们将计算的键添加到动作中:
rule NaxosR_attempt2:
[
In(X),
Fr(~eskR),
!Ltk($R, lkR)
]
--[ SessionKey($R, kR ) ]->//计算会话密钥
[
Out( 'g'^h1(< ~eskR, lkR >) )
]
kR的计算在上面还没有具体说明。我们可以将上面规则中的kR替换为完全展开的,但这会降低可读性。相反,我们使用let绑定来避免重复并减少可能的不匹配。此外,对于密钥计算,我们需要通信伙伴$I的公钥,我们将其绑定到一个唯一的线程标识符~tid;我们使用生成的操作事实来指定安全属性,这将在下一节中看到。这导致:
rule NaxosR_attempt3:
let
exR = h1(< ~eskR, lkR >)//先定义exR,后面会用到(简化)
hkr = 'g'^exR//向I发送的消息
kR = h2(< pkI^exR, X^lkR, X^exR, $I, $R >)//会话密钥
in
[
In(X),
Fr( ~eskR ),
Fr( ~tid ),
!Ltk($R, lkR),
!Pk($I, pkI)//持久事实,$I的公钥
]
--[ SessionKey( ~tid, $R, $I, kR ) ]->
[
Out( hkr )
]
上述规则准确地为响应者角色建模,并计算相应的密钥。
我们注意到一个进一步的优化,帮助Tamarin的向后搜索。NaxosR_attempt3中,规则指定lkR可以用任何术语实例化,因此也可以用非新鲜术语实例化。然而,由于密钥生成规则是产生Ltk事实的唯一规则,并且它将始终为密钥使用新值,因此很明显,在系统的任何可达状态中,lkR只能通过新值实例化。因此我们可以把lkR标记为新鲜类型,因此用~lkR代替它。
rule NaxosR:
let
exR = h1(< ~eskR, ~lkR >)
hkr = 'g'^exR
kR = h2(< pkI^exR, X^~lkR, X^exR, $I, $R >)
in
[
In(X),
Fr( ~eskR ),
Fr( ~tid ),
!Ltk($R, ~lkR),
!Pk($I, pkI)
]
--[ SessionKey( ~tid, $R, $I, kR ) ]->
[
Out( hkr )
]
我们稍后将看到,上述规则足以对基本安全属性进行建模。
对Naxos启动器角色进行建模
Naxos协议的发起者角色包括发送消息和等待响应。
在启动器等待响应时,其他代理也可能执行一些步骤。因此,我们使用两条规则对启动器进行建模第一条规则对启动启动器角色、生成新值并发送适当消息的代理进行建模。和前面一样,我们使用let绑定来简化表示,并使用~lkI而不是lkI,因为我们知道Ltk事实只以一个新值作为第二个参数生成
rule NaxosI_1_attempt1:
let exI = h1(<~eskI, ~lkI >)
hkI = 'g'^exI
in
[ Fr( ~eskI ),
!Ltk( $I, ~lkI ) ]
-->
[ Out( hkI ) ]
使用状态事实来模拟进程A
触发前一条规则后,启动器将等待响应消息。我们仍然需要对第二部分建模,其中接收响应并计算密钥。要对启动器规则的第二部分进行建模,我们必须能够指定它先于第一部分,并使用特定的参数。直观地说,我们必须在转换系统的状态中存储有一个启动线程,它已经执行了带有特定参数的第一次发送,因此它可以继续它上次的操作。
为了对此建模,我们引入了一个新的事实,我们通常将其称为状态事实:一个表明某个进程或线程在其执行过程中处于特定点的事实,有效地作为程序计数器和进程或线程内存内容的容器运行。
由于可以并行地存在任意数量的启动器,我们需要为它们的每个状态事实提供一个唯一的句柄。
下面我们将提供启动器第一条规则的更新版本,该规则生成状态事实Init_1,并为该规则的每个实例引入唯一的线程标识符~tid。
rule NaxosI_1:
let exI = h1(<~eskI, ~lkI >)
hkI = 'g'^exI
in
[ Fr( ~eskI ),
Fr( ~tid ),
!Ltk( $I, ~lkI ) ]
-->
[ Init_1( ~tid, $I, $R, ~lkI, ~eskI ),
Out( hkI ) ]
请注意,状态事实有几个参数:唯一的线程标识符 ~tid、代理身份 $I 和 $R、代理的长期私人密钥 ~lkI 和私人指数。这样,我们就可以指定第二条启动规则了。
rule NaxosI_2:
let
exI = h1(< ~eskI, ~lkI >)
kI = h2(< Y^~lkI, pkR^exI, Y^exI, $I, $R >)
in
[ Init_1( ~tid, $I, $R, ~lkI , ~eskI),
!Pk( $R, pkR ),
In( Y ) ]
--[ SessionKey( ~tid, $I, $R, kI ) ]->
[]
第二条规则要求从网络接收消息Y,同时还要求先前已生成了一条发起者事实。该规则然后消耗这个事实,并且由于协议中没有进一步的步骤,因此不需要输出类似的事实。因为Init_1事实是用相同的参数实例化的,所以第二步将使用相同的代理标识和第一步计算的指数exI。
因此,完整的示例变成:
theory Naxos
begin
builtins: diffie-hellman
functions: h1/1
functions: h2/1
rule Generate_DH_key_pair:
[ Fr(~x) ]
-->
[ !Pk($A,'g'^~x)
, Out('g'^~x)
, !Ltk($A,~x)
]
rule NaxosR:
let
exR = h1(< ~eskR, ~lkR >)
hkr = 'g'^exR
kR = h2(< pkI^exR, X^~lkR, X^exR, $I, $R >)
in
[
In(X),
Fr( ~eskR ),
Fr( ~tid ),
!Ltk($R, ~lkR),
!Pk($I, pkI)
]
--[ SessionKey( ~tid, $R, $I, kR ) ]->
[
Out( hkr )
]
rule NaxosI_1:
let exI = h1(<~eskI, ~lkI >)
hkI = 'g'^exI
in
[ Fr( ~eskI ),
Fr( ~tid ),
!Ltk( $I, ~lkI ) ]
-->
[ Init_1( ~tid, $I, $R, ~lkI, ~eskI ),
Out( hkI ) ]
rule NaxosI_2:
let
exI = h1(< ~eskI, ~lkI >)
kI = h2(< Y^~lkI, pkR^exI, Y^exI, $I, $R >)
in
[ Init_1( ~tid, $I, $R, ~lkI , ~eskI),
!Pk( $R, pkR ),
In( Y ) ]
--[ SessionKey( ~tid, $I, $R, kI ) ]->
[]
end
注意,协议描述只指定了一个模型,而没有指定它可能满足哪些属性。
我们将在下一节中讨论这些问题。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【论文笔记】BiFormer: Vision Transformer with Bi-Level Routing Attention
- 如何利用firewalld抵御DDOS攻击
- 最强开源中英双语大模型发布,340亿参数超越Llama2-70B !
- element-ui表单验证时undefined (reading ‘validate‘)
- Report the POCV Coefficient and Derating
- 弹性各向异性后处理软件 ElATools(二)
- 前端开发如何在自己项目中引用iconfont图标
- 使用git工具把项目文件上传到github 的操作
- 基于计算机视觉的棋盘图像识别
- 【Spring】SpringBoot 统一功能处理