数据探查系列：如何进行有意义的探索性数据分析（EDA）

发布时间：2023年12月27日

如何进行有意义的探索性数据分析（EDA）

1 | 设置

1.1 导入库

# 导入所需的库
import numpy as np
import pandas as pd
import seaborn as sns
import plotly.express as px
import tkinter
from matplotlib import pyplot as plt
from sklearn.model_selection import cross_val_score
from collections import Counter
# 设置seaborn的样式为ticks，并将上下文设置为talk
sns.set(style="ticks", context="talk")


<a id="1.2"></a>
## <b>1.2 <span style='color:#F1A424'>导入数据</span></b>


```python
# 读取训练数据和测试数据
try:
    # 尝试从指定路径读取训练数据和测试数据
    raw_train = pd.read_csv('/kaggle/input/playground-series-s3e4/train.csv', index_col='id')
    raw_test = pd.read_csv('/kaggle/input/playground-series-s3e4/test.csv', index_col='id')
except:
    # 如果指定路径读取失败，则从当前路径读取训练数据和测试数据
    raw_train = pd.read_csv('train.csv', index_col='id')
    raw_test = pd.read_csv('test.csv', index_col='id')

1.3 数据集特征

比赛的数据集（包括训练集和测试集）是从一个在信用卡欺诈检测（https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud）上训练的深度学习模型生成的。特征分布与原始数据集接近，但并非完全相同。请随意将原始数据集用作比赛的一部分，既可以探索差异，也可以查看是否将原始数据集纳入训练可以提高模型性能。

请注意，与之前的Tabular Tuesdays数据集相比，这个比赛的基础数据集要大得多，因此可能包含更多的伪像。

https://www.kaggle.com/competitions/playground-series-s3e4/overview

1.4 数据集属性

数据集说明

该数据集仅包含经过PCA转换的数值型输入变量。不幸的是，由于保密问题，我们无法提供原始特征和更多关于数据的背景信息。特征V1、V2、…、V28是通过PCA获得的主成分，唯一没有经过PCA转换的特征是’Time’和’Amount’。特征’Time’表示每个交易与数据集中第一笔交易之间经过的秒数。特征’Amount’表示交易金额，该特征可以用于基于示例的成本敏感学习。特征’Class’是响应变量，如果是欺诈交易则取值为1，否则为0。

Id - 每行的唯一标识符。
Time - 该交易与数据集中第一笔交易之间经过的秒数
V1-V28 - 经过降维处理以保护用户身份和敏感特征的特征
Amount - 交易金额
Class - 目标类别（1表示欺诈交易，0表示真实交易）

🔝返回目录🔝

2 | 探索训练集和测试集

训练数据集中的观察结果：

共有32列：30列连续型变量，0列分类变量，1列id和1列目标变量
共有219129行
类别是目标变量
没有缺失值

测试数据集中的观察结果：

共有31列：30列连续型数据，0列分类数据和1列id
共有146087行
没有缺失值

2.1 训练数据集 - 快速概览

# 查看训练数据的前几行
raw_train.head()

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V21	V22	V23	V24	V25	V26	V27	V28	Amount	Class
id
0	0.0	2.074329	-0.129425	-1.137418	0.412846	-0.192638	-1.210144	0.110697	-0.263477	0.742144	...	-0.334701	-0.887840	0.336701	-0.110835	-0.291459	0.207733	-0.076576	-0.059577	1.98	0
1	0.0	1.998827	-1.250891	-0.520969	-0.894539	-1.122528	-0.270866	-1.029289	0.050198	-0.109948	...	0.054848	-0.038367	0.133518	-0.461928	-0.465491	-0.464655	-0.009413	-0.038238	84.00	0
2	0.0	0.091535	1.004517	-0.223445	-0.435249	0.667548	-0.988351	0.948146	-0.084789	-0.042027	...	-0.326725	-0.803736	0.154495	0.951233	-0.506919	0.085046	0.224458	0.087356	2.69	0
3	0.0	1.979649	-0.184949	-1.064206	0.120125	-0.215238	-0.648829	-0.087826	-0.035367	0.885838	...	-0.095514	-0.079792	0.167701	-0.042939	0.000799	-0.096148	-0.057780	-0.073839	1.00	0
4	0.0	1.025898	-0.171827	1.203717	1.243900	-0.636572	1.099074	-0.938651	0.569239	0.692665	...	0.099157	0.608908	0.027901	-0.262813	0.257834	-0.252829	0.108338	0.021051	1.00	0

5 rows × 31 columns

2.2 训练数据集 - 基本统计信息

# 使用describe()函数对raw_train进行描述性统计分析
raw_train.describe()

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V21	V22	V23	V24	V25	V26	V27	V28	Amount	Class
count	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	...	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000	219129.000000
mean	62377.415376	0.096008	0.048345	0.592102	0.069273	-0.161555	0.133688	-0.128224	0.149534	-0.048337	...	-0.031064	-0.050852	-0.050531	-0.002992	0.124005	0.009881	0.014034	0.017313	66.359803	0.002140
std	25620.348569	1.395425	1.159805	1.132884	1.253125	1.069530	1.202411	0.817207	0.716212	1.054143	...	0.422777	0.597812	0.318175	0.593100	0.406741	0.473867	0.233355	0.164859	150.795017	0.046214
min	0.000000	-29.807725	-44.247914	-19.722872	-5.263650	-37.591259	-25.659750	-31.179799	-28.903442	-8.756951	...	-14.689621	-8.748979	-11.958588	-2.836285	-3.958591	-1.858672	-9.234767	-4.551680	0.000000	0.000000
25%	47933.000000	-0.846135	-0.573728	-0.027154	-0.769256	-0.847346	-0.631835	-0.646730	-0.095948	-0.711444	...	-0.190418	-0.473099	-0.174478	-0.332540	-0.126080	-0.318330	-0.050983	-0.009512	5.990000	0.000000
50%	63189.000000	0.385913	0.046937	0.735895	0.064856	-0.229929	-0.087778	-0.098970	0.111219	-0.131323	...	-0.042858	-0.032856	-0.063307	0.038708	0.145934	-0.086388	0.015905	0.022163	21.900000	0.000000
75%	77519.000000	1.190661	0.814145	1.306110	0.919353	0.356856	0.482388	0.385567	0.390976	0.583715	...	0.109187	0.354910	0.060221	0.394566	0.402926	0.253869	0.076814	0.066987	68.930000	0.000000
max	120580.000000	2.430494	16.068473	6.145578	12.547997	34.581260	16.233967	39.824099	18.270586	13.423914	...	22.062945	6.163541	12.734391	4.572739	3.111624	3.402344	13.123618	23.263746	7475.000000	1.000000

8 rows × 31 columns

2.3 测试数据集 - 快速概览

raw_test.head()

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V20	V21	V22	V23	V24	V25	V26	V27	V28	Amount
id
219129	120580.0	2.115519	-0.691809	-1.305514	-0.685655	-0.641265	-0.764784	-0.924262	-0.023030	-0.230126	...	0.067367	0.241708	0.682524	0.037769	-0.546859	-0.123055	-0.084889	0.004720	-0.021944	29.95
219130	120580.0	1.743525	-1.681429	-0.547387	-1.061113	-0.695825	2.458824	-1.632859	1.073529	1.068183	...	0.441788	0.543278	1.294571	0.309541	3.703925	-0.242579	0.068708	0.002629	0.064690	163.50
219131	120580.0	2.205568	-1.571445	-0.238965	-1.662517	-1.652324	-0.054701	-1.682064	0.105613	-1.177858	...	-0.366906	-0.131527	0.086623	0.291375	0.739087	-0.543006	-0.297813	0.043699	-0.037855	16.00
219132	120580.0	1.989728	-0.972909	-1.938259	-1.440129	-0.166855	-0.794048	0.252889	-0.399789	2.079398	...	-0.049136	-0.080115	-0.010732	-0.038550	0.656830	0.343470	-0.627529	-0.024338	-0.036143	120.98
219133	120580.0	-1.943548	-1.668761	0.363601	-0.977610	2.684779	-2.037681	0.039709	-0.048895	-0.281749	...	0.391627	0.083389	-0.306918	0.247822	-0.391799	-0.790716	-0.025706	0.330758	0.335537	1.98

5 rows × 30 columns

2.4 测试数据集 - 基本统计信息

# 使用describe()函数对raw_test数据进行描述性统计分析
raw_test.describe()

	Time	V1	V2	V3	V4	V5	V6	V7	V8	V9	...	V20	V21	V22	V23	V24	V25	V26	V27	V28	Amount
count	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	...	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000	146087.000000
mean	144637.928166	0.512929	-0.013098	-0.697478	-0.273258	0.321856	-0.050204	0.073419	0.043803	-0.071620	...	-0.056678	0.044729	0.175461	0.018471	0.016029	-0.118352	-0.015199	0.006236	0.002035	66.182463
std	14258.025396	1.628455	1.247749	1.292522	1.365752	1.146215	1.332880	0.946681	0.749513	0.924996	...	0.458364	0.449017	0.710704	0.359597	0.633929	0.479720	0.446154	0.255935	0.174613	153.151535
min	120580.000000	-34.755944	-37.803827	-18.934952	-5.497560	-25.639591	-14.133040	-18.715915	-26.926164	-4.823352	...	-26.412867	-13.087263	-5.392649	-12.814296	-2.789084	-3.361564	-1.743223	-9.412538	-8.262339	0.000000
25%	132698.000000	-0.679988	-0.715885	-1.619268	-1.021205	-0.418547	-0.891441	-0.570042	-0.231824	-0.634695	...	-0.237529	-0.166715	-0.393667	-0.135059	-0.368957	-0.409938	-0.284914	-0.066037	-0.057447	5.990000
50%	144493.000000	0.285798	0.009058	-0.719060	-0.482945	0.306851	-0.372813	0.118545	0.014979	-0.075909	...	-0.096729	0.058393	0.250169	0.017835	0.029727	-0.142325	-0.069342	-0.003539	-0.026955	21.790000
75%	156140.000000	1.974015	0.827420	0.073874	0.369725	0.955997	0.302724	0.734503	0.296969	0.513770	...	0.065753	0.244817	0.749555	0.167514	0.562138	0.182937	0.216632	0.069334	0.066954	66.000000
max	172790.000000	2.452901	12.390128	4.492640	11.232928	24.352818	16.596635	27.023955	12.098322	7.888980	...	15.829261	15.333546	5.771245	17.481609	4.541724	4.555960	3.374748	12.673968	13.093229	4630.600000

8 rows × 30 columns

🔝返回目录🔝

3 | 特征分布

# 获取数值型特征列
numeric_columns = (list(raw_train.loc[:, 'Time':'Amount']))

# 创建一个图形对象
fig = plt.figure(figsize=(20, 50))

# 设置子图的行数和列数
rows, cols = 10, 3

# 遍历数值型特征列
for idx, num in enumerate(numeric_columns[:30]):
    # 在图形对象中添加子图
    ax = fig.add_subplot(rows, cols, idx+1)
    
    # 设置网格线的透明度和轴
    ax.grid(alpha = 0.7, axis ="both")
    
    # 绘制训练集的核密度估计曲线
    sns.kdeplot(x = num, fill = True, color ="#3386FF", linewidth=0.6, data = raw_train, label = "Train")
    
    # 绘制测试集的核密度估计曲线
    sns.kdeplot(x = num, fill = True, color ="#EFB000", linewidth=0.6, data = raw_test, label = "Test")      
    
    # 设置x轴标签
    ax.set_xlabel(num)
    
    # 添加图例
    ax.legend()

# 调整子图的布局
fig.tight_layout()

# 显示图形对象
fig.show()

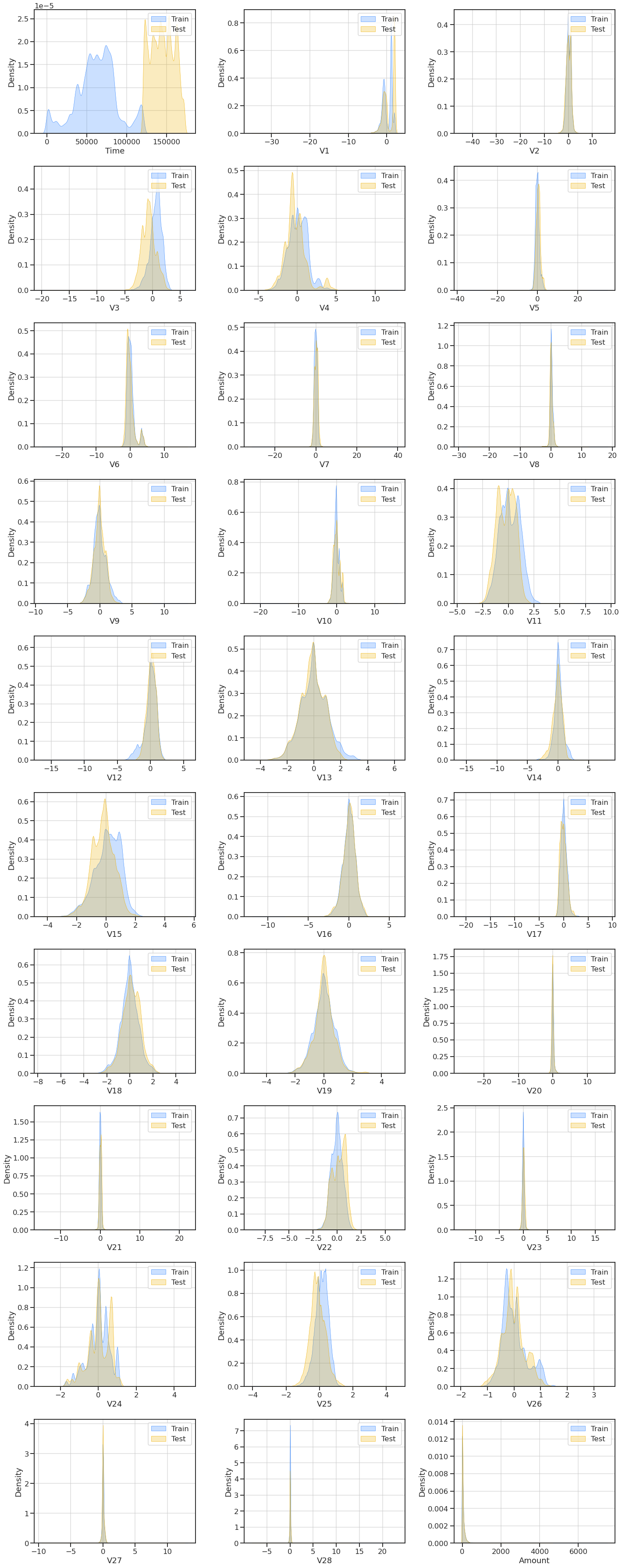
对于训练集和测试集来说，“时间”（Time）的分布非常不同。这可能会导致严重的问题，因为算法将更容易地区分这些集合。

我们可以通过将时间分解为一天中的小时特征或删除它来转换时间。

# 从原始训练数据中删除'Time'列，得到训练数据集
train_df = raw_train.drop('Time', axis=1)

# 从原始测试数据中删除'Time'列，得到测试数据集
test_df = raw_test.drop('Time', axis=1)

🔝返回目录🔝

4 | 数据不平衡检查 - 为什么它很重要

# 创建一个包含两种颜色的调色板
palette = ["#ADD8E6","#EFB000"]

# 给饼图添加注释
# 获取训练数据集中每个类别的数量，并转换为列表
l1 = list(train_df['Class'].value_counts())
# 计算每个类别在总数中的比例，并乘以100，得到饼图的数值
pie_values = [l1[0] / sum(l1) * 100, l1[1] / sum(l1) * 100]

# 创建一个包含两个子图的图形，设置图形大小为(20, 7)
fig = plt.subplots(nrows=1, ncols=2, figsize=(20, 7))

# 在第一个子图中绘制饼图
plt.subplot(1, 2, 1)
plt.pie(pie_values, labels=['Genuine', 'Fraud'], 
        autopct='%1.2f%%',  # 设置饼图上显示的百分比格式
        startangle=90,  # 设置饼图的起始角度为90度
        explode=(0.1, 0.1),  # 设置饼图中每个扇区的偏移量，使其突出显示
        colors=palette,  # 设置饼图的颜色
        wedgeprops={'edgecolor': 'black', 'linewidth': 1, 'antialiased': True})  # 设置饼图的边缘颜色、线宽和抗锯齿效果
plt.title('Fraud vs Genuine transactions in train data set %');  # 设置子图标题

# 在第二个子图中绘制柱状图
plt.subplot(1, 2, 2)
ax = sns.countplot(data=train_df, 
                   x='Class', 
                   palette=palette,  # 设置柱状图的颜色
                   edgecolor='black')  # 设置柱状图的边缘颜色
for i in ax.containers:
    ax.bar_label(i,)  # 在每个柱状图上添加标签，显示每个类别的数量
ax.set_xticklabels(['Genuine', 'Fraud'])  # 设置x轴刻度标签为类别名称

plt.title('Fraud vs Genuine transactions in train data set')  # 设置子图标题
plt.show()  # 显示图形

4.1 不平衡数据需要不同的方法

我们有**99.8%的真实交易（218,660笔），只有0.214%**的欺诈交易（469笔）！

这意味着盲猜（押注真实交易）将给我们**99.8%**的准确率。

不要使用准确率作为不平衡数据集的度量标准 - 它通常会非常高且具有误导性（您可以使用AUC-ROC、召回率、F1分数等）。
考虑利用欠采样或过采样技术。
在训练测试拆分期间使用分层拆分。
在处理异常值时要特别小心（您可以删除有意义的信息）。

5 | 我们应该删除异常值吗？

5.1 检查训练数据集中的异常值

# 定义一个函数，用于绘制数据集中数值型变量的箱线图
# 参数包括数据集、数值型变量列表、行数、列数和总标题
def boxplots_custom(dataset, columns_list, rows, cols, suptitle):
    # 创建一个绘图对象和子图对象
    fig, axs = plt.subplots(rows, cols, sharey=True, figsize=(16,25))
    # 设置总标题
    fig.suptitle(suptitle,y=1, size=25)
    # 将子图对象展平为一维数组
    axs = axs.flatten()
    # 遍历数值型变量列表，绘制每个变量的箱线图
    for i, data in enumerate(columns_list):
        # 使用seaborn库的boxplot函数绘制箱线图
        sns.boxplot(data=dataset[data], orient='h', ax=axs[i])
        # 设置每个子图的标题，包括变量名和偏度值
        axs[i].set_title(data + ', skewness is: '+str(round(dataset[data].skew(axis = 0, skipna = True),2)))
        
# 调用函数，绘制训练集中数值型变量的箱线图
boxplots_custom(dataset=train_df, columns_list=numeric_columns, rows=10, cols=3, suptitle='Boxplots for each variable')
# 调整子图的布局
plt.tight_layout()

看起来我们在异常值方面有很大的问题：

巨大的异常值；
高度偏斜的数据；
很多异常值。

5.2 四分位距 (IQR)

Tukey’s (1977) 方法用于检测偏斜或非钟形分布的数据中的异常值，因为它不做分布假设。然而，对于小样本大小，Tukey’s 方法可能不适用。一般规则是，不在 (Q1 - 1.5 IQR) 和 (Q3 + 1.5 IQR) 范围内的任何值都是异常值，并可以被移除。

四分位距离（IQR）是最常用的异常值检测和移除方法之一。

过程：

找到第一四分位数，Q1。
找到第三四分位数，Q3。
计算 IQR。IQR = Q3-Q1。
将正常数据范围定义为下限为 Q1-1.5 IQR，上限为 Q3+1.5 IQR。

def IQR_method(df, n, features):
    """
    使用Tukey IQR方法，接受一个数据框并返回一个索引列表，该列表对应于包含n个以上异常值的观测值。
    """
    outlier_list = [] # 初始化一个空列表，用于存储异常值的索引
    
    for column in features: # 遍历每个特征列
        # 第一四分位数（25%）
        Q1 = np.percentile(df[column], 25)
        # 第三四分位数（75%）
        Q3 = np.percentile(df[column],75)
        # 四分位距（IQR）
        IQR = Q3 - Q1
        # 异常值步长
        outlier_step = 1.5 * IQR
        # 确定异常值索引列表
        outlier_list_column = df[(df[column] < Q1 - outlier_step) | (df[column] > Q3 + outlier_step )].index
        # 将异常值索引列表添加到总的异常值列表中
        outlier_list.extend(outlier_list_column)
        
    # 选择包含多于n个异常值的观测值
    outlier_list = Counter(outlier_list)        
    multiple_outliers = list(k for k, v in outlier_list.items() if v > n)
    
    # 计算低于和高于边界值的记录数
    out1 = df[df[column] < Q1 - outlier_step]
    out2 = df[df[column] > Q3 + outlier_step]
    
    # 打印删除的异常值总数
    print('删除的异常值总数为：', out1.shape[0]+out2.shape[0])
    
    return multiple_outliers

5.3 检测和删除异常值


# 使用IQR方法检测并处理离群值
Outliers_IQR = IQR_method(train_df, 1, numeric_columns)

# 在原始数据集中删除离群值，并重新设置索引
df_out = train_df.drop(Outliers_IQR, axis=0).reset_index(drop=True)

Total number of deleted outliers is: 20617

5.4我们做了什么？

# 打印输出在删除异常值之前数据集中的欺诈交易数量
print ('The amount of frauds in df before dropping outliers: ', len(train_df[train_df['Class'] == 1]))

# 打印输出在删除异常值之后数据集中的欺诈交易数量
print ('The amount of frauds in df after dropping outliers: ', len(df_out[df_out['Class'] == 1]))

The amount of frauds in df before dropping outliers:  469
The amount of frauds in df after dropping outliers:  188

通过删除异常值，我们丢失了约**40%的非常重要的数据！我们不应该这样做！**

我们有几个选择，但对于这项研究，我们将回到删除异常值之前的阶段。这里一个非常有趣的选择是创建一个仅包含异常值的新数据框。您可以在此处查看此方法的结果：

https://www.kaggle.com/code/marcinrutecki/credit-card-fraud-detection-tensorflow

🔝返回目录🔝

6 | 处理重复值

# 打印数据集中重复值的数量
print('Number of duplicated values in dataset: ', train_df.duplicated().sum())

Number of duplicated values in dataset:  94

# 复制train_df数据框并赋值给df
df = train_df.copy()

# 删除df数据框中的重复行
df.drop_duplicates(inplace=True)

# 打印提示信息，表示重复值已成功删除
print("Duplicated values dropped succesfully")

# 打印100个"*"，用于分隔输出信息
print("*" * 100)

Duplicated values dropped succesfully
****************************************************************************************************

让我们检查一下是否有任何欺诈交易被删除了。这很重要，因为如果是这样的话，我们应该再次考虑它们是否是真正的重复交易。

# 打印在去除重复值之前df中的欺诈数量
print ('The amount of frauds in df before dropping duplicates: ', len(train_df[train_df['Class'] == 1]))

# 打印在去除重复值之后df中的欺诈数量
print ('The amount of frauds in df after dropping duplicates: ', len(df[df['Class'] == 1]))

The amount of frauds in df before dropping duplicates:  469
The amount of frauds in df after dropping duplicates:  469

如我们所见，我们没有丢失任何重要的数据。

🔝返回目录🔝

7 | 相关性

# 创建一个11x11的图像
plt.figure(figsize=(11, 11))

# 计算数据集的相关系数矩阵
corr = df.corr()

# 创建一个与相关系数矩阵相同形状的布尔矩阵，上三角为True，下三角为False
mask = np.triu(np.ones_like(corr, dtype=bool))

# 使用热力图可视化相关系数矩阵，只显示上三角部分，颜色映射为viridis
sns.heatmap(corr, mask=mask, robust=True, center=0, square=True, cmap="viridis", linewidths=.6)

# 设置图像标题
plt.title('Correlation Table')

# 显示图像
plt.show()


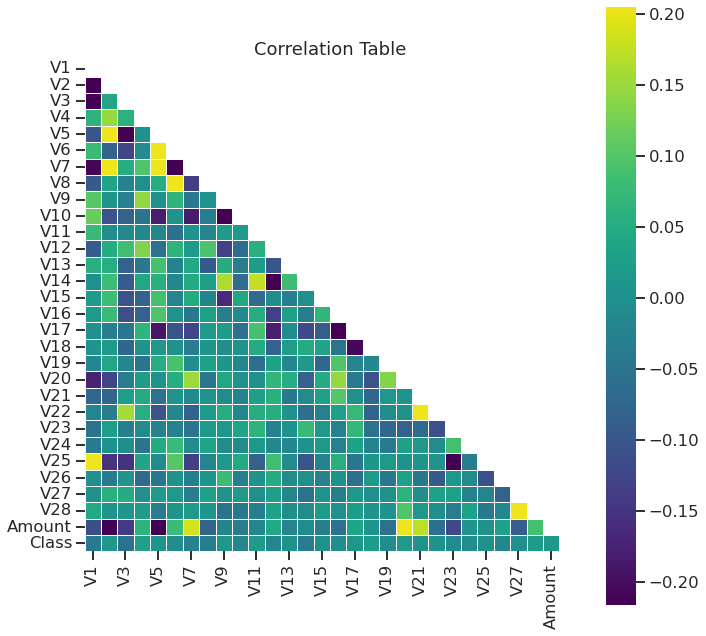
# 创建一个大小为7x4的图形
plt.figure(figsize=(7,4))

# 计算数据框df中'Class'列与其他列的相关系数，并取绝对值，按照相关系数的大小进行排序，并绘制柱状图
d = df.corr()['Class'][:-1].abs().sort_values().plot(kind='bar', title='Highly correlated features with Class')

🔝返回目录🔝

8 | 更多可视化



# 设置绘图大小
plt.figure(figsize=(10,10))

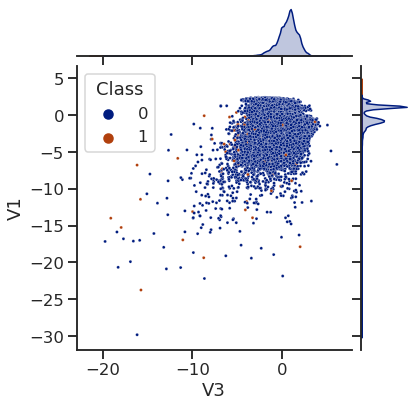
# 绘制联合分布图，x轴为V3，y轴为V1，颜色按照Class分类，数据来源为df，调色板为dark，点的大小为9
sns.jointplot(x='V3', y='V1',hue='Class', data=df, palette='dark', s=9)

<seaborn.axisgrid.JointGrid at 0x7f36c0b01f50>




<Figure size 720x720 with 0 Axes>


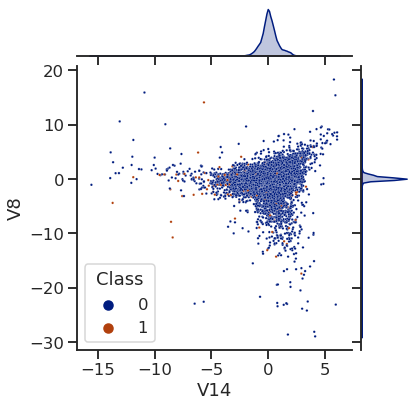
# 设置图形大小
plt.figure(figsize=(10,10))

# 创建联合图
# x轴为特征V14，y轴为特征V8
# 根据Class变量的不同值对数据点进行着色
# 使用'dark'调色板进行着色
# 设置数据点的大小为6
sns.jointplot(x='V14', y='V8', hue='Class', data=df, palette='dark', s=6)

<seaborn.axisgrid.JointGrid at 0x7f36c0b01050>




<Figure size 720x720 with 0 Axes>

🔝返回目录🔝

文章来源:https://blog.csdn.net/wjjc1017/article/details/135252396
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！