4.6 BOUNDARY CHECKS
我们现在扩展了tile矩阵乘法内核,以处理具有任意宽度的矩阵。扩展必须允许内核正确处理宽度不是tile宽度倍数的矩阵。通过更改图4.14中的示例至3×3 M、N和P矩阵,图4.18创建了矩阵的宽度为3,不是tile宽度(2)的倍数。图4.18显示了block0,.0.第1阶段的内存访问模式。Thread0,1和thread1,1,我将尝试加载不存在的M元素。同样,thread1,0和thread1,1将尝试访问N个不存在的元素。
访问不存在的元素在两个方面存在问题。访问行末尾的非现有元素(M通过thred1.0和thread,1访问,在图4.18中。)将对不正确的元素进行处理。在我们的示例中,线程将尝试访问M0.3和M1.3,两者都不存在。在这种情况下,这些内存负载会发生什么?为了回答这个问题,我们需要回到二维矩阵的线性化布局。在线性化布局中,M0.2之后的元素是M1.0。虽然thred01正在尝试访问M0.3,但它将获得M1,0.在子内积计算中使用该值肯定会腐蚀输出值。
从我们到目前为止的讨论来看,有问题的访问似乎只出现在线程执行的最后阶段。这一观察表明,可以在平铺内核执行的最后阶段采取特殊行动来解决这个问题。不幸的是,所有阶段都可能出现有问题的访问。图4.19显示了0阶段block1,1的内存访问模式。我们看到thread1,0和thread1,1试图访问不存在的M元素Ms3,0和Ms3.1,而thread0.1和thread1,1试图访问N0,3和N1,3,它们不存在。
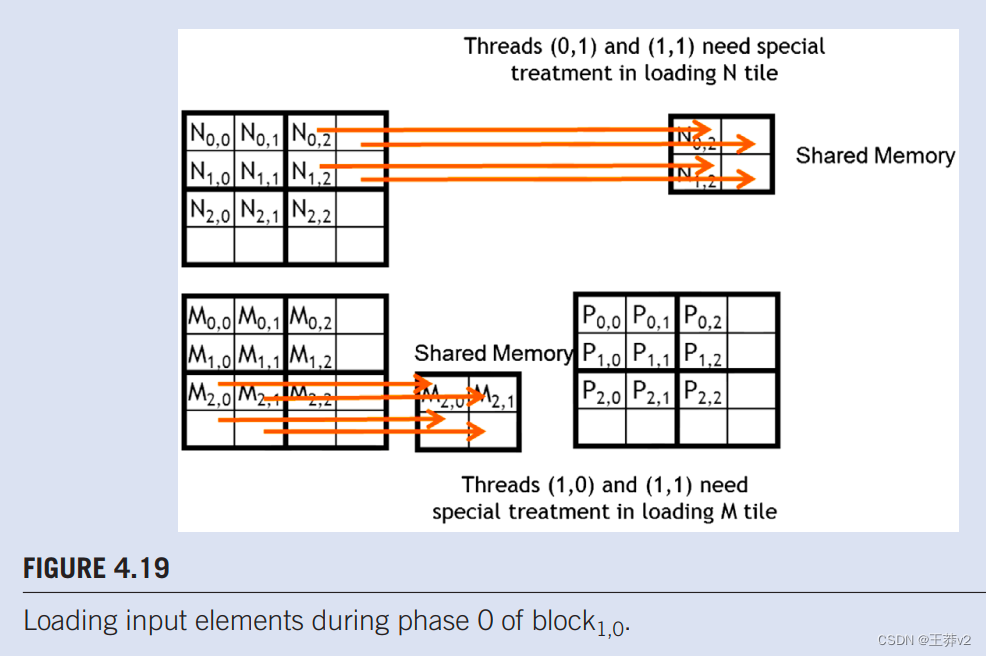
请注意,无法通过排除不计算有效P元素的线程来防止这些有问题的访问。例如,block1,1中的thread1,0不计算任何有效的P元素。然而,它需要在0阶段加载M2,1。此外,一些计算有效P元素的线程将尝试访问不存在的M或N元素。如图4.18所示。0,0 block的,thread0,1计算一个有效的P元素P0.1。然而,它试图在第1阶段访问不存在的M0,3。这些观察表明,需要进行不同的边界条件测试,以加载M tiles、加载N tiles和计算/存储P元素。
我们从加载输入tile的边界测试条件开始。当线程打算加载输入tile元素时,它应该测试该输入元素的有效性,这很容易通过检查y和x索引来完成。举例来说,在图4.16中的第9行,线性化索引来自行的y索引和phTILE _WIDTH + tx的x索引。边界条件测试是两个索引都小于宽度:(Row<Width) && (phTILE_WIDTH+tx)<Width。如果条件满足,线程应该加载M元素。读者应该验证加载N元素的条件测试是(ph*TILE_WIDTH+ty)<Width && Col<Width。
如果条件不满足,线程不应加载元素,在这种情况下,问题是应该将什么放在共享内存位置。答案是0.0,如果在内积计算中使用,这个值不会造成任何伤害。如果任何线程在计算其内积时使用此0.0值,则不会观察到内积值的变化。
最后,线程只有在负责计算有效的P元素时才应存储其最终的内积值。此条件的测试是(Row < Width)&&(Col < Width)。带有附加边界条件检查的内核代码如图4.20.所示。
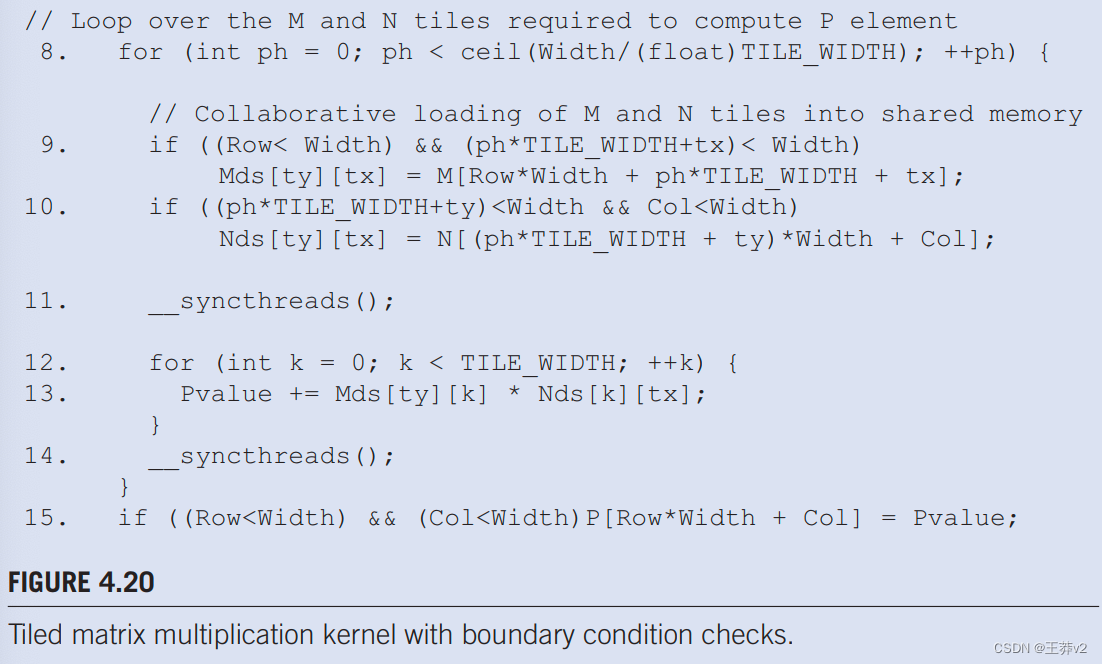
Tile(瓷砖)的思想是将大的矩阵操作分解为更小的子矩阵(或“瓷砖”)的操作。这样做可以充分利用CUDA架构的共享内存,这是一种比全局内存访问速度快得多的内存类型。通过使用共享内存,可以显著减少对全局内存的访问次数,从而减少内存延迟,并提高整体的内存带宽效率。
选择TILE_WIDTH的原因包括:
- 共享内存限制:每个CUDA核心的共享内存是有限的。例如,早期的CUDA硬件每个block只有16KB的共享内存。如果你尝试一次性加载整个矩阵,你可能会超过这个限制,从而导致错误或性能下降。
- 线程块大小限制:CUDA核心对每个线程块可以包含的线程数量也有限制。例如,如果每个核心允许的最大线程块大小是1024个线程,那么使用32×32(即1024)的
TILE_WIDTH就是这个限制的上限。如果尝试一次性加载更大的瓷砖,你将无法在一个线程块中为每个瓷砖元素分配一个线程。 - 内存带宽利用:通过分块(tiling)可以使得每次从全局内存中加载的数据都能被多次使用,这样可以减少内存访问的次数,从而更高效地利用内存带宽。
- 缓存局部性:共享内存可以被看作是用户可控的缓存。使用瓷砖技术可以增加缓存命中率,因为一旦一个瓷砖被加载到共享内存中,它的数据可以被同一个线程块中的多个线程重复使用。
- 计算与内存访问的重叠:在计算当前瓷砖的同时,下一个瓷砖的数据可以从全局内存中预取,这样可以隐藏内存访问延迟。
为什么不一次性加载整个矩阵:
-
共享内存大小:如上所述,共享内存的大小是有限的,通常不足以存储整个矩阵。
-
线程资源管理:更小的瓷砖允许更细粒度的线程管理和更高的线程并行度。
-
内存访问模式:一次性加载可能会导致内存访问模式不佳,从而降低缓存效率。
因此,TILE_WIDTH的选择是一个权衡的结果,它需要考虑硬件的限制、内存的效率和算法的并行性。通常,开发人员会根据具体的硬件配置来调整TILE_WIDTH的大小,以达到最佳性能。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 动态规划 - 509.斐波那契数(C#和C实现)
- 【数据结构】八大排序之计数排序算法
- 如何制作一本电子版时尚杂志
- 计算机毕业设计SSM基于的医院预约挂号管理系统768de9【附源码】
- 字符数组的sizeof和strlen
- 使用微信读书高效阅读论文,自带翻译功能。
- 将本地文件传到远程仓库
- k8s修改/etc/resolve.conf导致容器域名解析失败
- 【Zabbix】使用 Grafana 统一监控展示并对接Zabbix v6
- imgaug库指南(11):从入门到精通的【图像增强】之旅