LeetCode-数组-矩阵问题-中等难度

@[toc]

矩阵

矩阵是二维数组相关的应用题型，常见的有矩阵水平翻转、矩阵对角线翻转、矩阵遍历等。

1. 重塑矩阵

1.1 题目描述

leetcode跳转：566. 重塑矩阵

1.2 方法一：简单模拟

借助一个一维数组用来保持按行列遍历的结果，然后再按照新的行列遍历生成即可。

public int[][] matrixReshape(int[][] mat, int r, int c) {
    int m = mat.length;
    int n = mat[0].length;
    if (r * c != m * n) {
        return mat;
    }

    // 按原行列遍历
    int[] temp = new int[r * c];
    int idx = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            temp[idx++] = mat[i][j];
        }
    }

    // 按新行列遍历
    int[][] ans = new int[r][c];
    idx = 0;
    for (int i = 0; i < r; i++) {
        for (int j = 0; j < c; j++) {
            ans[i][j] = temp[idx++];
        }
    }
    return ans;
}

1.3 方法二：原地遍历

方法一的在空间上需要额外开辟一个行×列大小的数组，实际上我们只需要根据行列遍历的一个公式即可完成。

假设有一个4×5的二维数组：

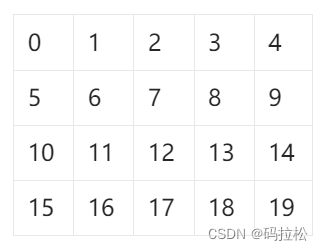
很明显，每一行的起始位置也就是：0、5、10、15 ，如果我们从下标0开始遍历，一直遍历到第19位的话，那么每一行的起始位置实际上就是：i / 5，而每一列就是i % 5。

所以，我们只需要完成的遍历一次数组的长度即可完成矩阵的重塑。

public int[][] matrixReshape(int[][] mat, int r, int c) {
    int m = mat.length;
    int n = mat[0].length;
    if (r * c != m * n) {
        return mat;
    }
    int[][] ans = new int[r][c];
    for (int i = 0; i < r * c; i++) {
        ans[i / c][i % c] = mat[i / n][i % n];
    }
    return ans;
}

2. 转置矩阵

2.1 题目描述

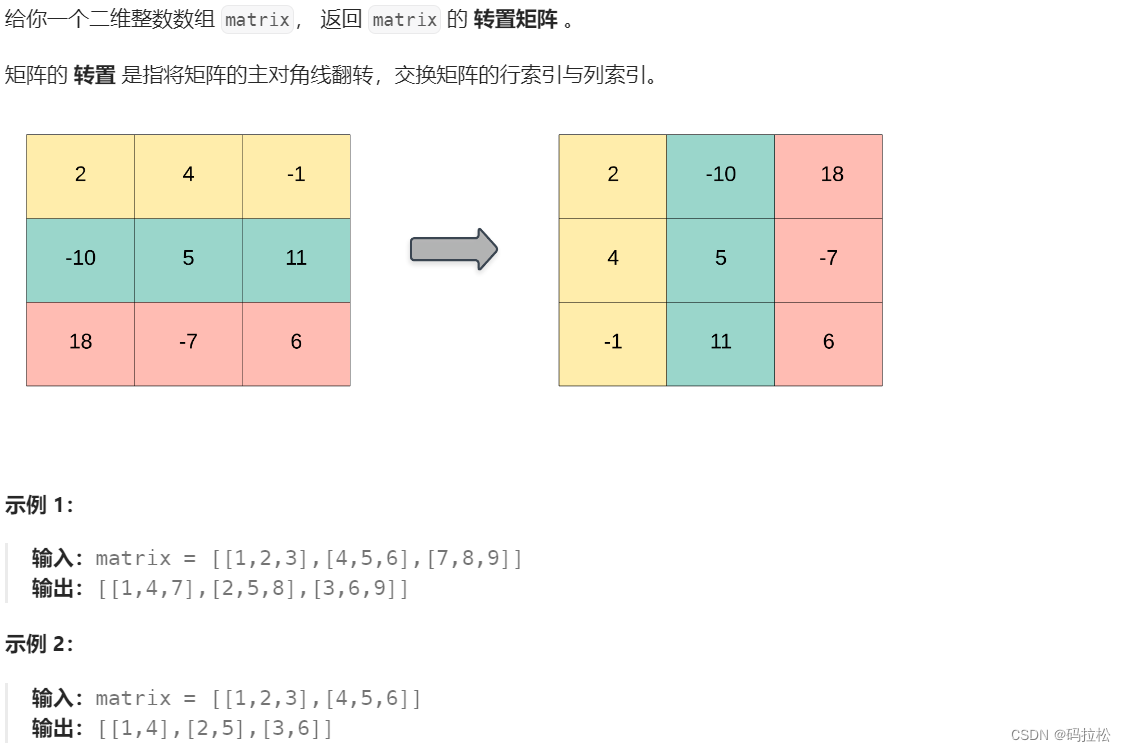
leetcode跳转：867. 转置矩阵

2.2 方法：模拟

按题意模拟即可，其实就是按行输出，变成按列输出而已。

class Solution {
    public int[][] transpose(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] ans = new int[n][m];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                ans[j][i] = matrix[i][j];
            }
        }
        return ans;
    }
}

3. 矩阵置零

3.1 题目描述

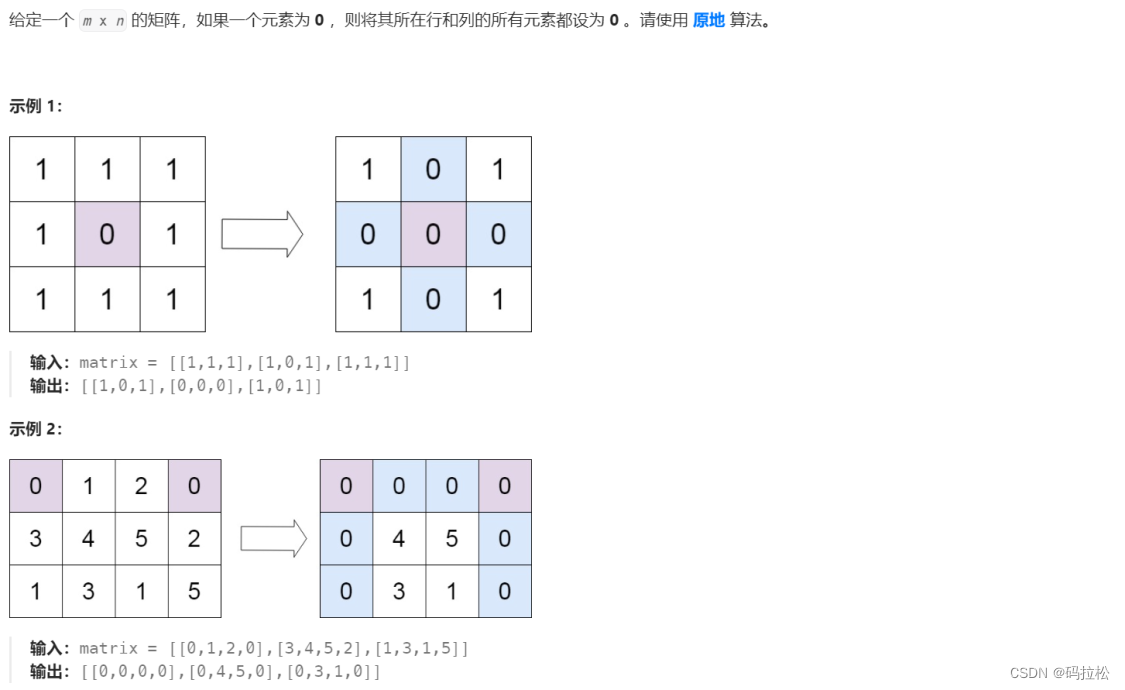
3.2 方法一：辅助标记

比较容易想到的方式就是，额外借助两个数组，用来标记哪些行、哪些列应该为零。

public void setZeroes(int[][] matrix) {
    int[] row = new int[matrix.length];
    int[] col = new int[matrix[0].length];
    for (int i = 0; i < matrix.length; i++) {
        for (int j = 0; j < matrix[i].length; j++) {
            // 原数组下标为0，则表示下标所在行、列都需要置为0
            if (matrix[i][j] == 0) {
                row[i] = 1;
                col[j] = 1;
            }
        }
    }
    for (int i = 0; i < matrix.length; i++) {
        for (int j = 0; j < matrix[i].length; j++) {
            // 如果行或列为0，则置为0
            if (row[i] == 1 || col[j] == 1) {
                matrix[i][j] = 0;
            }
        }
    }
}

3.3 方法二：原地算法

本题的难点就在于，算法要求你在不使用额外空间的条件下完成，所以很明显你必须直接在原数组上完成置零。
我们可以借助矩阵本身来实现标记。

比如有如下矩阵：

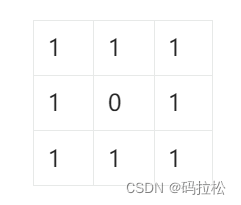
我们如果就用第一行和第一列作为标记项，当遍历到坐标(1,1)为0时，就可以标记(0,1)和(1,0)为0。

for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (matrix[i][j] == 0) {
            matrix[0][j] = matrix[i][0] = 0;
        }
    }
}

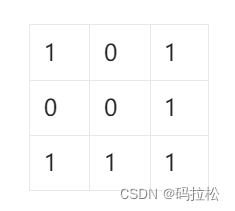
这样一次遍历结束后，我们再重新遍历一次，只要下标所属的第一行或者第一列为0，则直接置为0

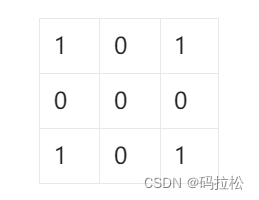
for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (matrix[0][j] == 0 || matrix[i][0] == 0) {
            matrix[i][j] = 0;
        }
    }
}

当然，还需要解决一个问题，就是第一行、第一列本身也有0的情况，比如像下面这样：

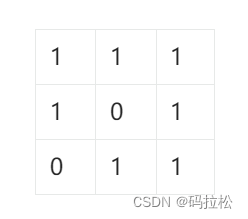
为了区分到底是本身就含有0，还是被其他坐标标记为0的情况，我们还需要预先记录一下第一行、第一列是否含有0。

boolean m0_flag = false;
boolean n0_flag = false;
for (int i = 0; i < m; i++) {
    if (matrix[i][0] == 0) {
        n0_flag = true;
        break;
    }
}
for (int i = 0; i < n; i++) {
    if (matrix[0][i] == 0) {
        m0_flag = true;
        break;
    }
}

最后完成其他坐标置0后，再处理第一行和第一列有零的情况即可。

if (m0_flag) {
    for (int i = 0; i < n; i++) {
        matrix[0][i] = 0;
    }
}
if (n0_flag) {
    for (int i = 0; i < m; i++) {
        matrix[i][0] = 0;
    }
}

完整代码实现如下：

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        boolean m0_flag = false;
        boolean n0_flag = false;
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                n0_flag = true;
                break;
            }
        }
        for (int i = 0; i < n; i++) {
            if (matrix[0][i] == 0) {
                m0_flag = true;
                break;
            }
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[0][j] = matrix[i][0] = 0;
                }
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[0][j] == 0 || matrix[i][0] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (m0_flag) {
            for (int i = 0; i < n; i++) {
                matrix[0][i] = 0;
            }
        }
        if (n0_flag) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

4. 旋转图像

4.1 题目描述

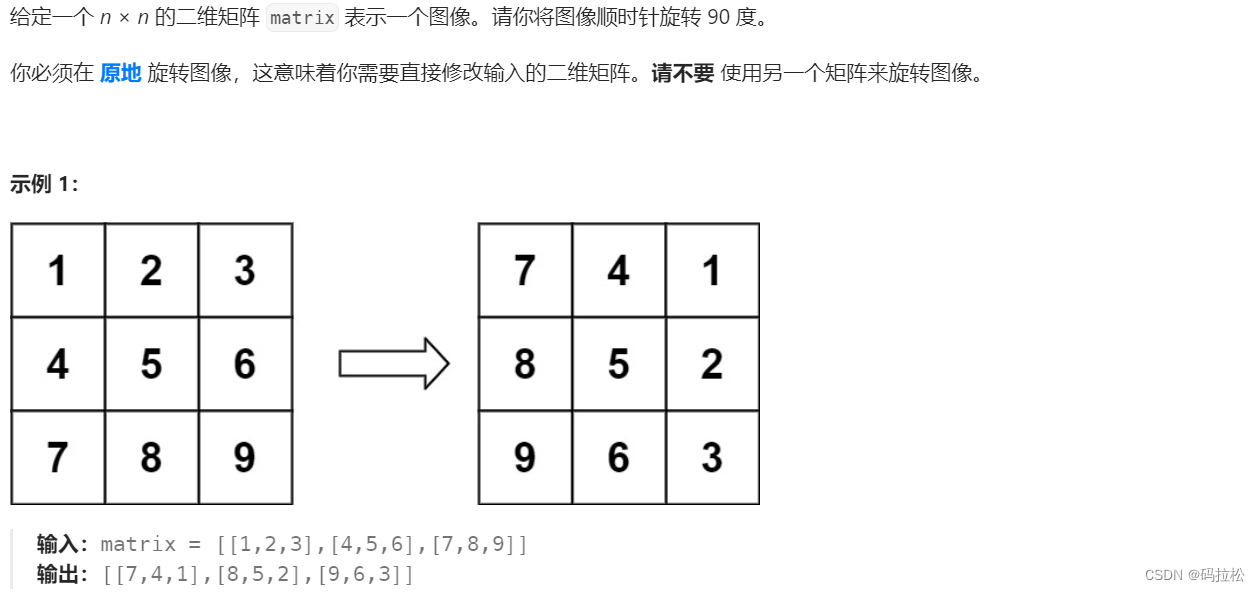
4.2 方法一：模拟一

先从最后一行开始，按行遍历：7,8,9,4,5,6,1,2,3，再从第一列开始，按列写入即可。

class Solution {
	public void rotate(int[][] matrix) {
		int n = matrix.length;
		int[][] helper = new int[n][n];
		for(int i = n - 1; i >= 0; i--){
			for(int j = 0; j < n; j++){
				helper[j][n - 1 - i] = matrix[i][j];
			}
		}

		for(int i = 0; i < n; i++){
			for(int j = 0; j < n; j++){
				matrix[i][j] = helper[i][j];
			}
		}
	}
}

4.3 方法二：模拟二

我们还可以只用一个一维数组来模拟这样的输出方式。

class Solution {
	public void rotate(int[][] matrix) {
		int n = matrix.length;
		int[] helper = new int[n * n];
		for(int i = 0; i < n; i++){
			for(int j = 0; j < n; j++){
				helper[n * i + j] = matrix[i][j];
			}
		}
		// helper：1 2 3 4 5 6 7 8 9
		// 从最后一行开始，按列遍历
		// 7 4 1
		// 8 5 2
		// 9 6 3
		int idx = helper.length - 1;
		for(int i = 0; i < n; i++){
			for(int j =  n - 1; j >= 0; j--){
				matrix[j][i] = helper[idx--];
			}
		}
	}
}

4.4 方法三：原地算法

按照本题要求，请你尝试在不占用额外内存空间的情况下完成旋转。

步骤一：我们可以先完成一次水平翻转，也就上下行交换。

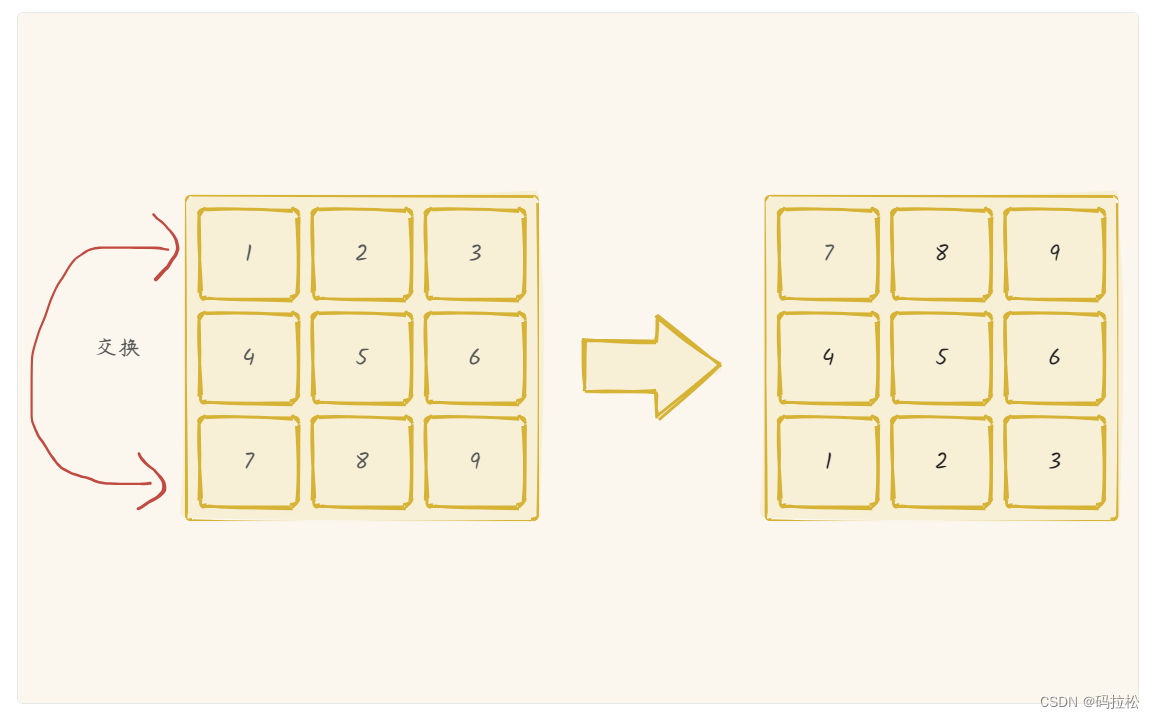
步骤二：然后再按照对角线进行翻转即可。

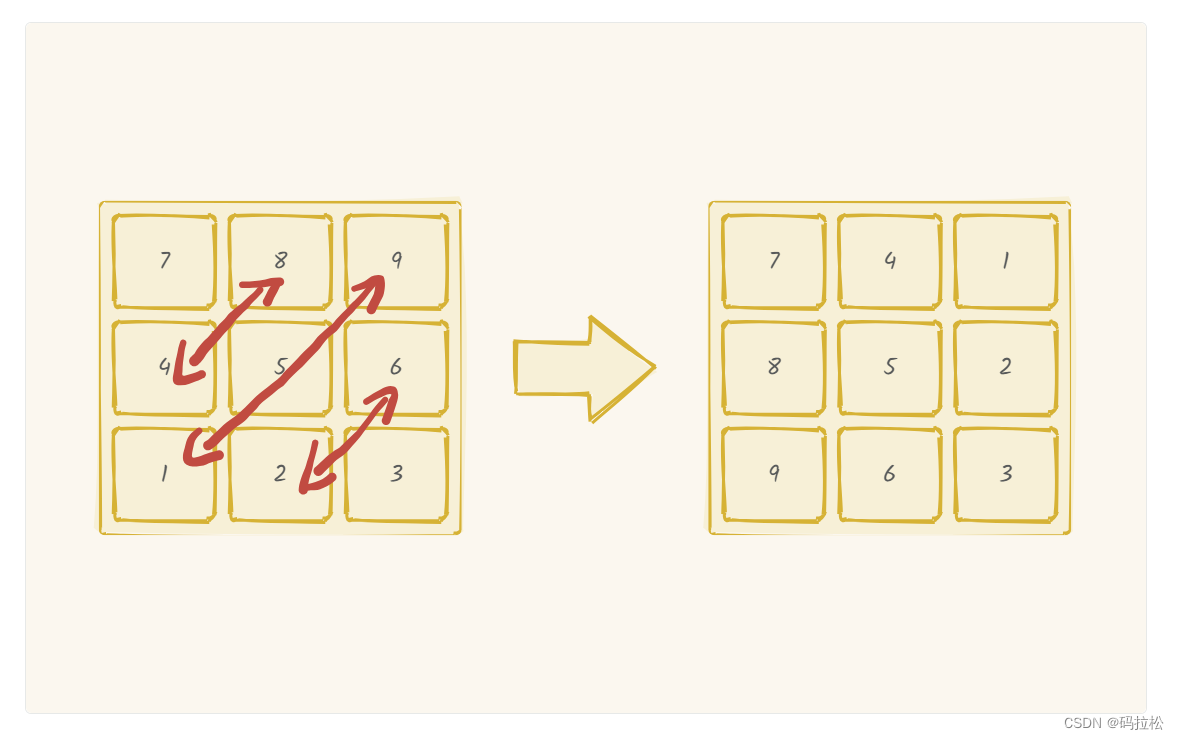
代码实现如下：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 水平翻转
        for(int i = 0; i < n / 2; i++){
            for(int j = 0; j < n; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = temp;
            }
        }
        
        // 对角线翻转
        for(int i = 0; i < n; i++){
            for(int j = i; j < n; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

5. 螺旋矩阵

5.1 题目描述

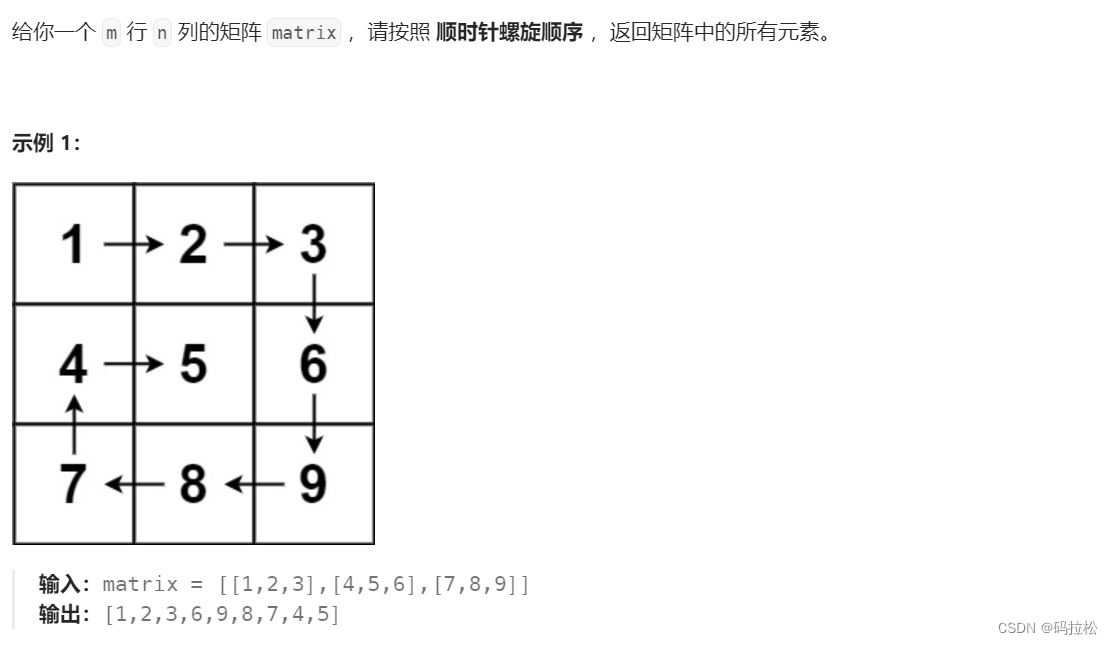
本题主要考察的还是编码和思维能力，按题意模拟即可，没有什么技巧可言。

我们采用按前进方向进行模拟，分别定义上下左右四个方向，那么前进路线以此就为：左→右、上→下、右→左、下→上

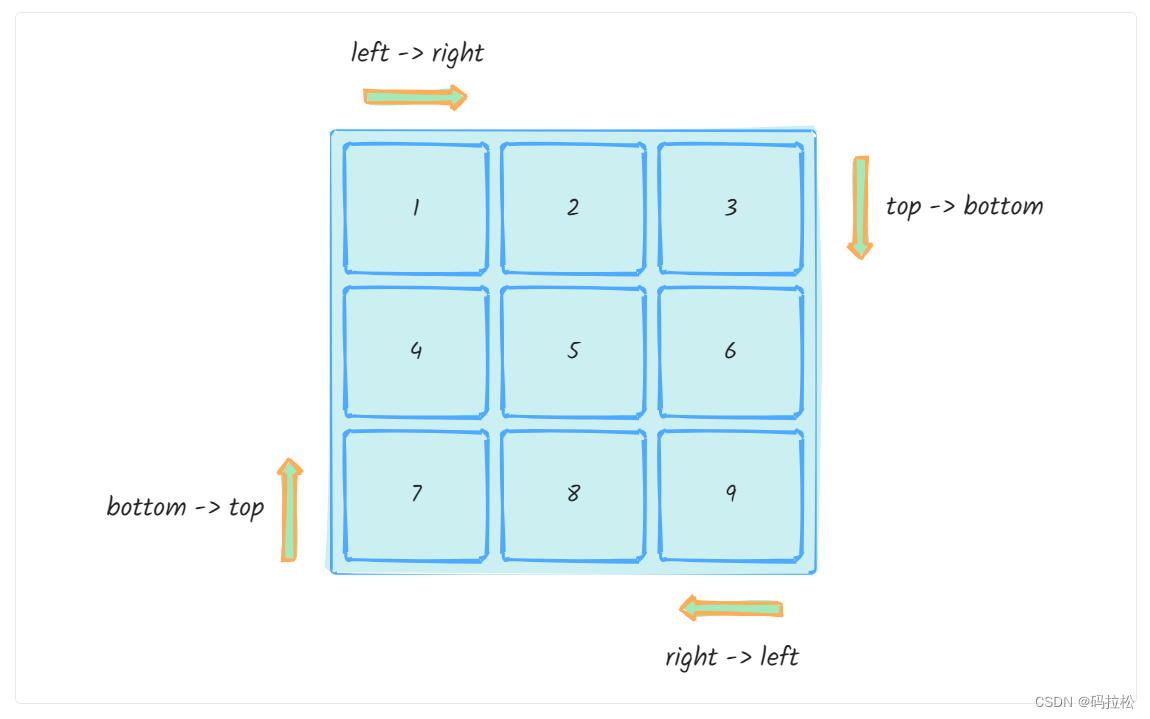
按照四个方向来模拟这个思路非常容易想到，关键在于能不能想的清楚四个方向分别表示的含义是什么？

下面给出四个方向的定义：

所以，从left走到right的方式如下所示：

for (int i = left; i <= right; i++) {
	ans.add(matrix[top][i]);
}

从top走到bottom的方式如下所示：

for (int i = top + 1; i <= bottom; i++) {
	ans.add(matrix[i][right]);
}

从right走到left的方式如下所示：

for (int i = right - 1; i > left; i--) {
	ans.add(matrix[bottom][i]);
}

最后，从bottom走到top的方式如下所示：

for (int i = bottom; i > top; i--) {
	ans.add(matrix[i][left]);
}

5.2 方法：模拟

public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int left = 0;
        int right = n - 1;
        int top = 0;
        int bottom = m - 1;
        // 用来记录已经走的步数
        int step = 0;
        List<Integer> ans = new ArrayList<>();
        while (step < m * n) {
            for (int i = left; i <= right; i++) {
                if (step < m * n) {
                    ans.add(matrix[top][i]);
                    step++;
                }
            }
            for (int i = top + 1; i <= bottom; i++) {
                if (step < m * n) {
                    ans.add(matrix[i][right]);
                    step++;
                }
            }
            for (int i = right - 1; i > left; i--) {
                if (step < m * n) {
                    ans.add(matrix[bottom][i]);
                    step++;
                }
            }
            for (int i = bottom; i > top; i--) {
                if (step < m * n) {
                    ans.add(matrix[i][left]);
                    step++;
                }
            }
            // 一圈走完以后，更新每个方向
            left++;
            right--;
            top++;
            bottom--;
        }
        return ans;
    }