刷题总结1.17 下午

第五题的平面图，偶图不理解

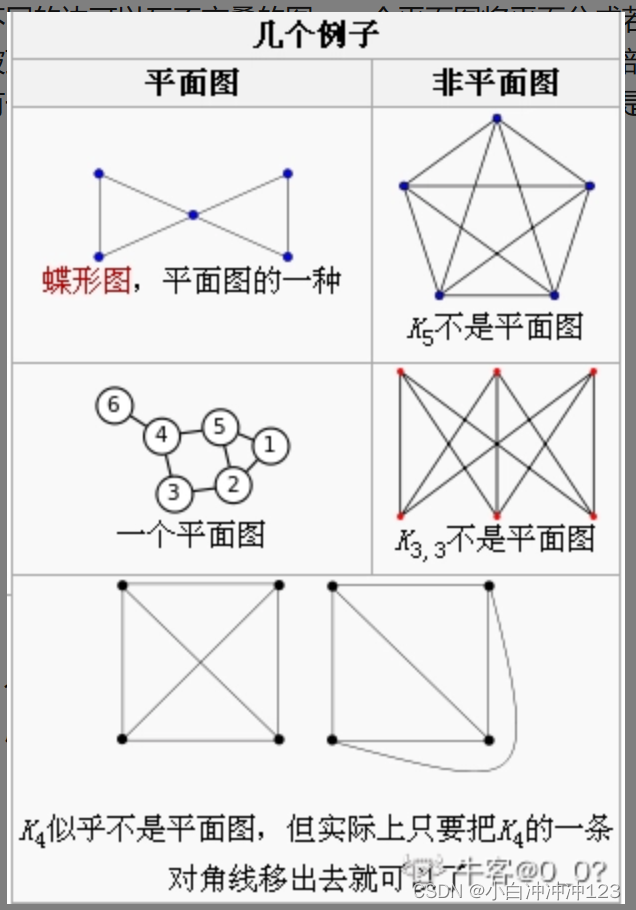
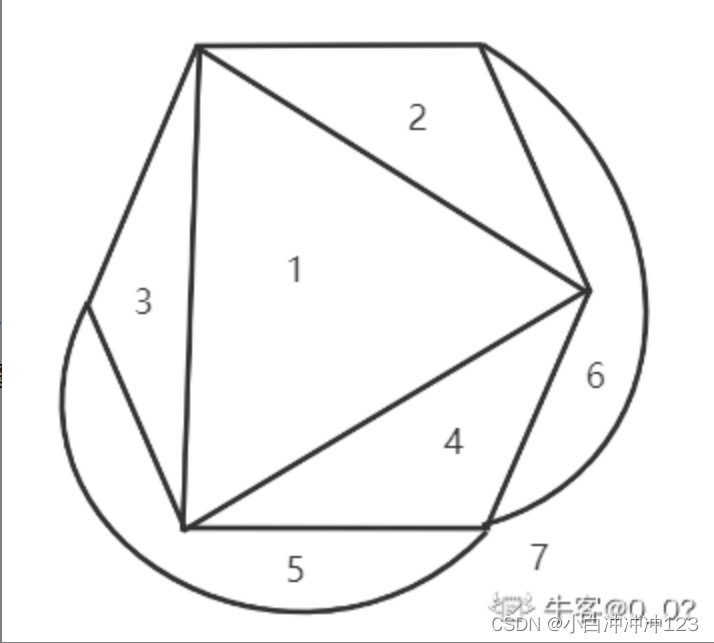
第三题为什么使用克鲁斯卡尔算法？

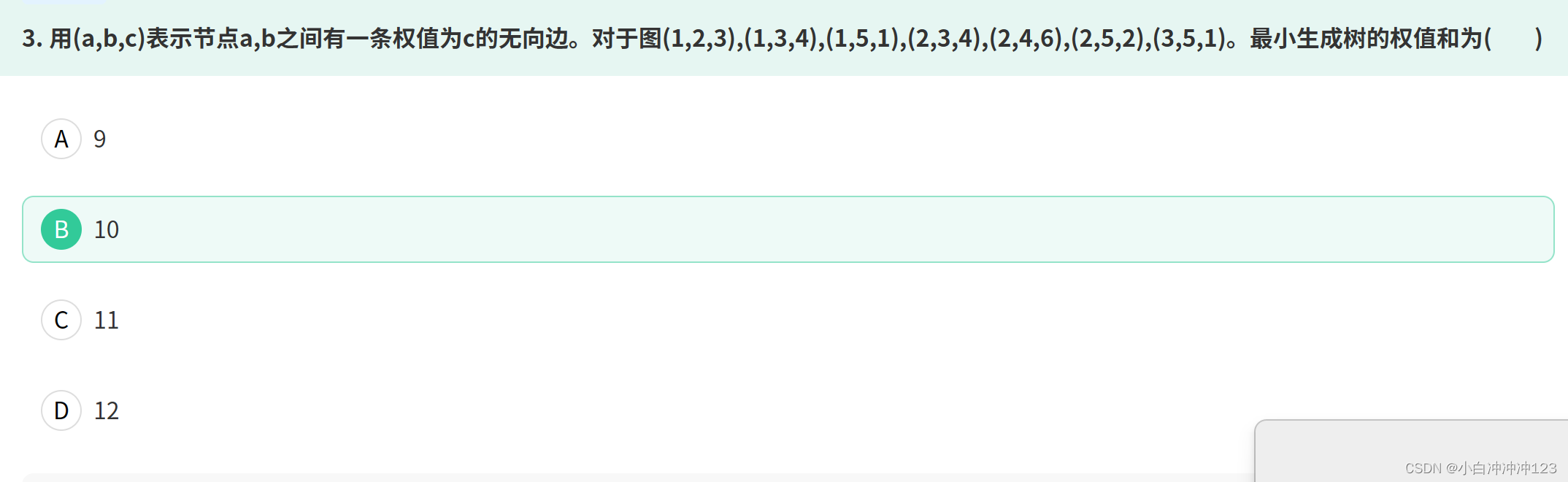
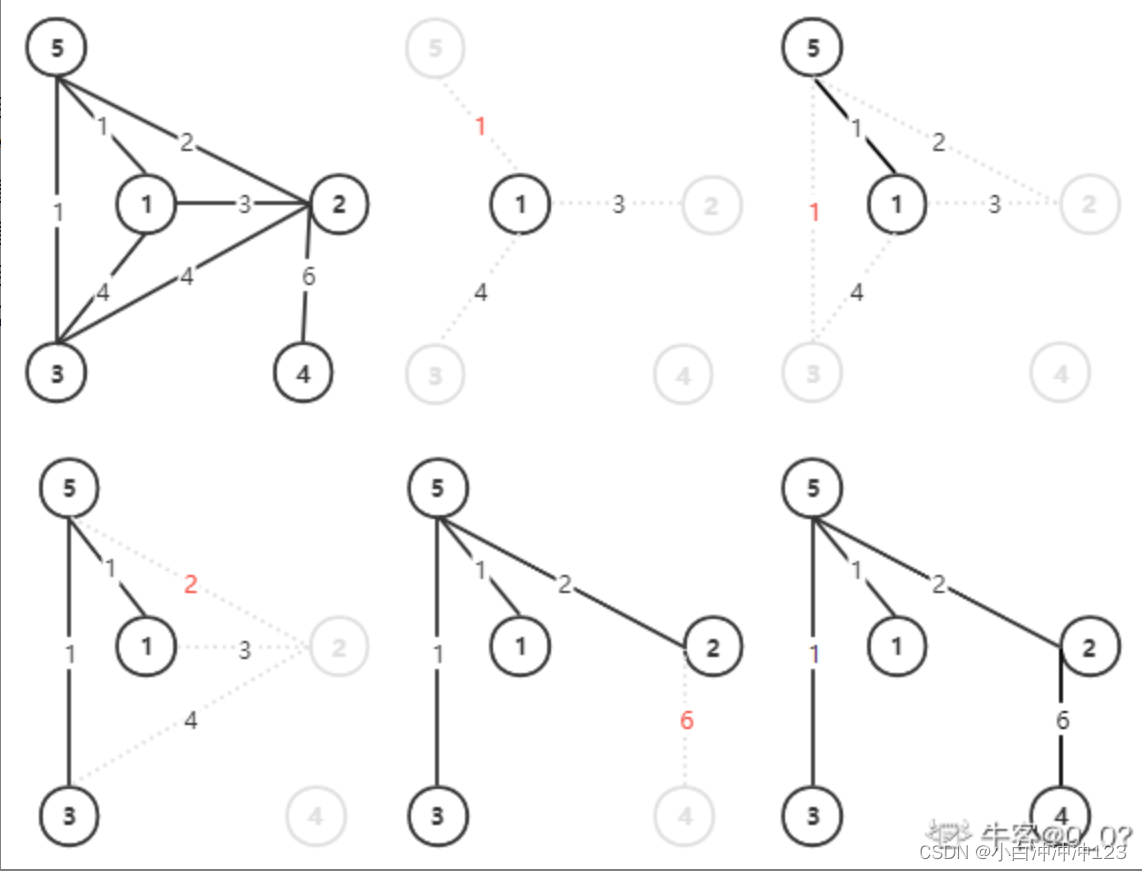
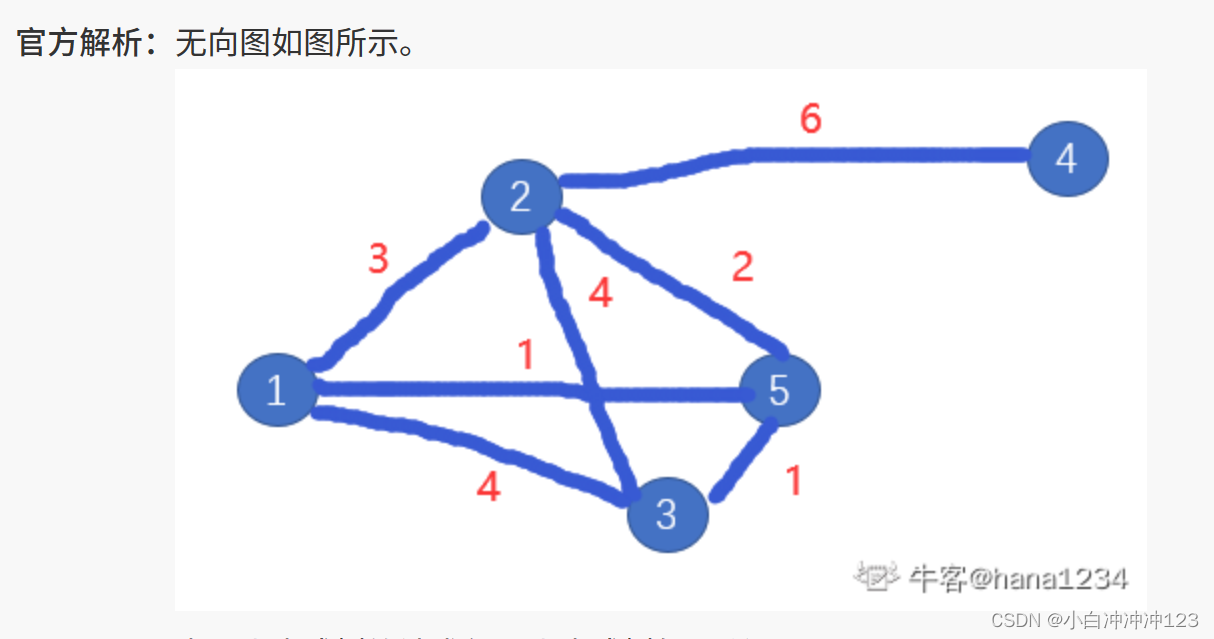
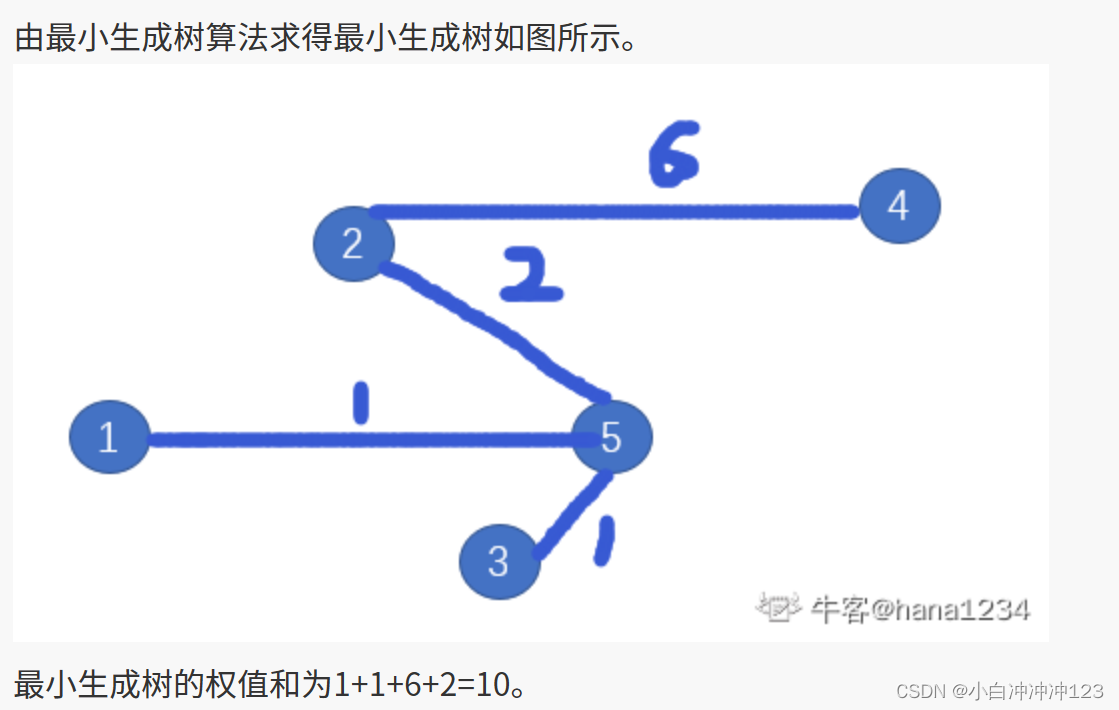
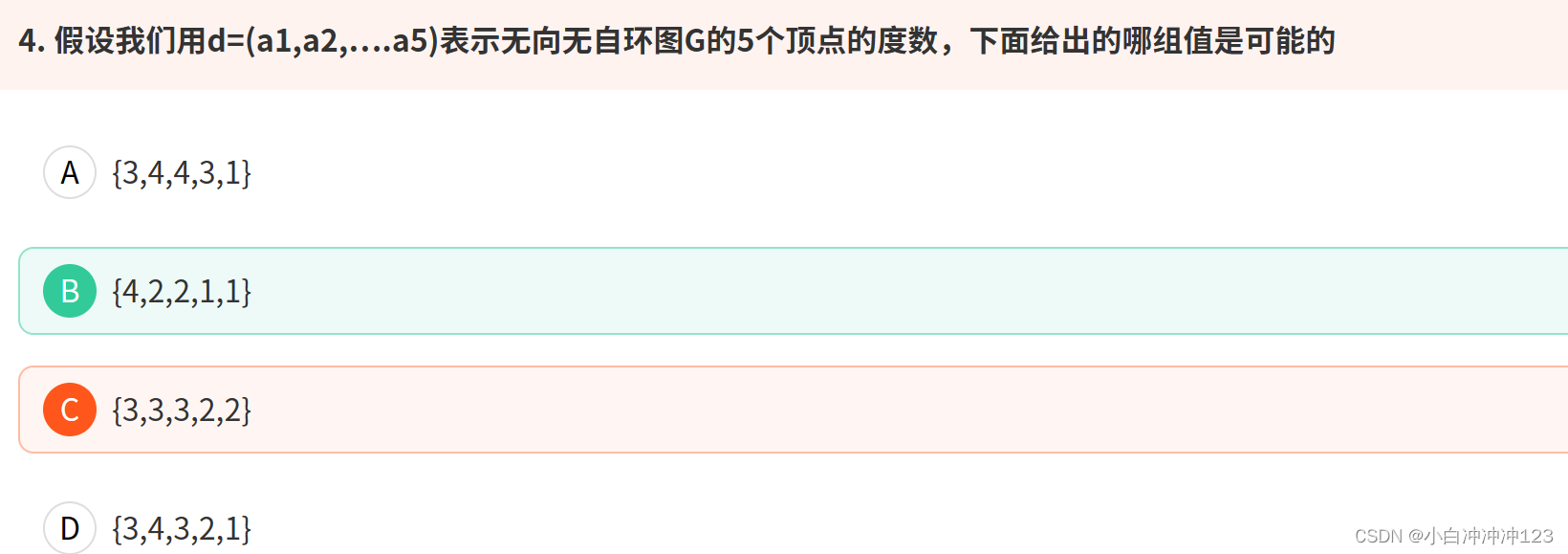
旅行商问题（Traveling Salesman Problem，TSP）是一个著名的组合优化问题，描述的是一个旅行商要在给定的一系列城市之间找到最短的路径，使得每个城市只访问一次，并最终回到起点城市。

旅行商变种问题是对旅行商问题的一些扩展或变化，通常包括以下几个方面：

1. 多旅行商问题（Multiple Traveling Salesman Problem，mTSP）：在这个问题中，有多个旅行商需要分别访问一系列城市，每个旅行商只能访问一次每个城市，并且所有旅行商最终都需要回到起点。

2. 权重旅行商问题（Weighted Traveling Salesman Problem，wTSP）：在这个问题中，每个城市之间的路径都有一个权重或成本，旅行商需要找到一条最短路径，使得路径上的权重之和最小。

3. 限制旅行商问题（Constrained Traveling Salesman Problem，CTSP）：在这个问题中，除了要找到最短路径外，还要满足一些其他的限制条件。例如，某些城市之间可能有一些限制，旅行商需要遵守这些限制。

4. 动态旅行商问题（Dynamic Traveling Salesman Problem，DTSP）：在这个问题中，城市之间的路径或权重可能会随着时间的推移而发生变化。旅行商需要在每次访问城市时重新计算最短路径。

这些是旅行商问题的一些常见的变种，每个变种都有不同的解决方法和算法。对于复杂的问题，通常需要使用启发式算法或元启发式算法来求解最优解。

以下是旅行商问题的一些变种问题：
1. 对称旅行商问题：所有城市之间的距离都是对称的，即从城市A到城市B的距离等于从城市B到城市A的距离。
2. 非对称旅行商问题：城市之间的距离是非对称的，即从城市A到城市B的距离可以不等于从城市B到城市A的距离。
3. 多旅行商问题：旅行商需要经过的城市被分成多个集合，每个集合由不同的旅行商访问。
4. 限制条件下的旅行商问题：添加了一些额外的限制，例如旅行商需要在特定的时间内完成旅行，或者需要遵循特定的路线规则等。

在同等顾客数量下，可行解数量最多的旅行商问题是多旅行商问题。因为多旅行商问题允许将城市划分为多个集合，将旅行任务分配给多个旅行商，从而增加了可行解的数量。其他变种问题都是将所有城市都由同一个旅行商访问，因此可行解的数量较少。

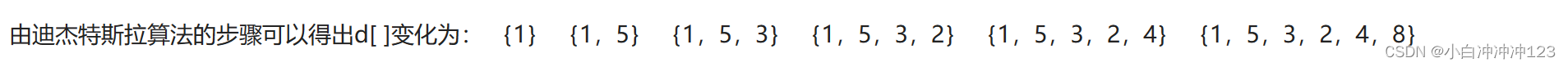
迪杰斯特拉算法和弗洛伊德算法都是用于求解最短路径的算法，但是它们的具体过程稍有不同。

迪杰斯特拉算法：
1. 初始化：将起点标记为已访问，距离值设为0，将其它顶点的距离值设为无穷大。
2. 遍历起点的邻接顶点，更新起点到邻接顶点的距离值。
3. 选择当前距离值最小的顶点作为下一个访问顶点，并标记为已访问。
4. 以新访问的顶点为中转点，更新和它相邻的未访问顶点的距离值，如果通过中转点到达未访问顶点的距离值更短，则更新距离值。
5. 重复第3步和第4步，直到所有顶点都被访问。

弗洛伊德算法：
1. 初始化：将图中的边权值赋给对应的距离矩阵。
2. 对距离矩阵进行n次迭代，其中n是图中顶点的个数。
3. 在每次迭代中，检查通过第k个顶点的路径是否存在更短的路径，如果存在则更新距离矩阵中的距离值。
4. 迭代完成后，距离矩阵中存储的就是任意两点之间的最短路径。

总结：迪杰斯特拉算法是以单源最短路径为目标，每次选择距离起点最近的顶点进行更新，直到所有顶点都被访问。而弗洛伊德算法是以所有点对之间的最短路径为目标，通过多次迭代更新距离矩阵，直到得到最终的最短路径结果。