84. 柱状图中最大的矩形
发布时间:2024年01月24日
单调栈(与接雨水类似)
思路关键:
要想找到第 i 位置最大面积是什么?
是以 i 为中心,向左找第一个小于 heights[i] 的位置 left_i;向右找第一个小于于 heights[i] 的位置 right_i,即最大面积为 heights[i] * (right_i - left_i -1),如下图所示:
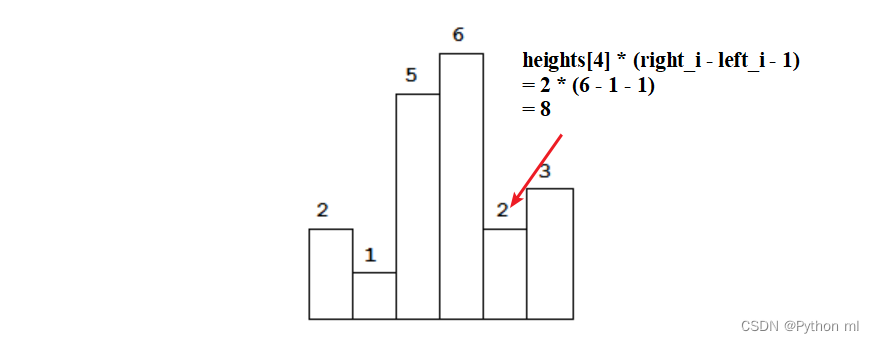
而找到左右两边第一个比heihts[i]小的位置可以用单调栈
- 递增的单调栈:在栈中递增则压入,所以栈中的上一个位置就是left_i
- 而当前遍历到第一个小于栈顶的位置则为以栈顶heights[cur]为高度的最大矩形的右边界
所以每次pop出的时候都会计算pop出元素位置的heights[cur]为高度的最大矩形面积。
时间复杂度:O(n),全部元素只会pop出一次
空间复杂度:O(n),一直递增则全部压入
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int>st;
//首尾填充0,避免边界条件讨论
heights.insert(heights.begin(),0);heights.push_back(0);
int ans=0;
for(int i=0;i<heights.size();++i){
//比栈顶元素小时 计算以柱子i为高度的矩形面积
while(!st.empty() && heights[st.top()]>heights[i]){
int cur = st.top(); //以height[cur]为高度的矩形
st.pop();
if(st.empty()) break;
int l = st.top(); //左边界为递增单调栈的上一个压入的位置
int r = i; //右边界为当前遍历的i
ans = max(ans, (r-l-1)*heights[cur]);
}
st.push(i); //(比他大的栈顶元素都pop出了)压入当前遍历位置
}
return ans;
}
};
文章来源:https://blog.csdn.net/m0_48711099/article/details/135829813
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【Java基础知识 16】禁止使用Lombok,在Lombok的加持下,“小狗”.equals(“老狗”) = true
- 密码学:一文看懂Base64算法
- 深圳服务器托管:降本增效,助力企业发展
- 数据结构与算法之二分查找
- C练习——模拟投掷6000次骰子
- Keil5如何生成反汇编文件
- 中国膜生物反应器市场预测与投资战略报告(2024版)
- 基于ChatGPT4+Python近红外光谱数据分析及机器学习与深度学习建模
- 手机上连网络转接app,电脑连接手机,共用网络转接app的办法
- java-sec-code中jwt