算法设计与分析复习笔记第五章回溯法

目录

回溯法的算法框架

0-1背包问题

n后问题

最优装载问题

旅行商问题

---

回溯法的算法框架

几种搜索方法

状态空间的搜索实际上是一种树的搜索，常用的方法有：

广度优先的搜索
从初始状态开始，逐层地进行搜索。

深度优先的搜索
从初始状态开始，逐个分枝地进行搜索。

启发式的搜索
从初始状态开始，每次选择最有可能达到终止状态的结点进行搜索。

三种搜索的优劣之处

广度优先搜索的优点是一定能找到解；缺点是空间复杂性和时间复杂性都大。

深度优先搜索的优点是空间复杂性和时间复杂性较小；缺点是不一定能找到解。

启发式搜索是最好优先的搜索，优点是一般来说能较快地找到解，即其时间复杂性更小；缺点是需要设计一个评价函数，并且评价函数的优劣决定了启发式搜索的优劣。

树搜索的一般形式

三种搜索的不同之处

树的三种搜索方法的不同就在于它们对表L使用了不同控制方式：

其中，深度优先搜索就是回溯法。

回溯法的形式化描述

回溯法的适用情形

有许多问题，当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时，往往要使用回溯法。

回溯法的基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。

回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。

回溯法的适用情形-举例

两类问题

存在性问题

求满足某些条件的一个或全部元组，如果不存在这样的元组算法应返回No；这些条件称为约束条件。

优化问题

给定一组约束条件，在满足约束条件的元组中求使某目标函数达到最大（小）值的元组。满足约束条件的元组称为问题的可行解。

回溯法的基本思想

回溯法从根结点出发，按照深度优先策略搜索（遍历）解空间树，搜索满足约束条件的解。

初始时，根结点成为一个活结点，同时也称为当前的扩展结点。在当前扩展结点处，搜索向纵深方向移至一个新结点。这个新结点成为一个新的活结点，并成为当前的扩展结点。如果在当前的扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为一个死结点（即不再是一个活节点）。此时，应往回移动（回溯）至最近的一个活结点处，并使这个活结点成为当前的扩展结点。

在搜索至树中任一结点时，先判断该结点对应的部分解是否满足约束条件，或者是否超出限界函数的界，也就是判断该结点是否包含问题的（最优）解，如果肯定不包含，则跳过对以该结点为根的子树的搜索，即所谓剪枝；否则，进入以该结点为根的子树，继续按照深度优先策略搜索。

在搜索过程中，通常采用两种策略避免无效搜索：

（1）用约束条件剪去得不到可行解的子树；
（2）用限界函数剪去得不到最优解的子树。

这两类函数统称为剪枝函数。

递归回溯法的一般形式（经常出现）

如何判断最后一个儿子？

若只要遍历解空间树上的结点，那么将各个结点按栈的方式控制便可实现深度为主的搜索。

但是在求解问题时，需要记录解的路径，在回溯时还需要删除结点和修改相应的信息。

栈中的结点是分层次的，而现在没有区分它们的层次。这就增加了回溯判断和操作的困难。

采用一个简洁有效的方法：设计一个末尾标记，每次压栈时，先压入末尾标记。

用末尾标记的迭代回溯

不可接受的结点

破坏了解的相容条件的结点

超出了状态空间的范围，或者说不满足约束条件的结点；

评价值很差的结点，即已经知道不可能获得解的结点；

已经存在于被考察的路径之中的结点，这种结点会造成搜索的死循环。

0-1背包问题

给定n个物品和一个背包。物品i的重量为wi，价值为vi，背包容量为c。问如何选择装入背包中的物品，使得装入背包的物品的价值最大？

在装入背包时，每种物品i只有两种选择，装入或者不装入，既不能装入多次，也不能只装入一部分。因此，此问题称为0-1背包问题。

如果在装入背包时，物品可以切割，即可以只装入一部分，这种情况下的问题称为背包问题。

0-1背包问题的表示方法

例：有n个物品的0-1背包问题，其可能解的表示方式有两种。

（1）可能解由一个不等长向量组成
当物品i(1≤i≤n)装入背包时，解向量中包含分量i，否则，解向量中不包含分量i。　
当n=3时，其解空间：　
{ ( ), (1), (2), (3), (1, 2), (1, 3), (2, 3), (1, 2, 3) }

（2）可能解由一个等长向量{x1, x2, …, xn}组成
xi=1(1≤i≤n)表示物品i装入背包，xi=0表示物品i没有装入背包。　
当n=3时，其解空间：　
{(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0), (1, 1, 1) }

0-1背包问题的实例

例如，对于n=3的0/1背包问题，三个物品的重量为{16, 15, 15}，价值为{45, 25, 25}，背包容量为30，从其解空间树的根结点开始搜索，搜索过程如下：

用回溯法解0-1背包问题

用一个数组P[n]存放目前取得的最优解，用变量V表示其价值；再用一个数组N[n]来产生新的解，用变量NV表示其价值，用变量W表示其重量。如果新解更优，则替代原来的最优解，否则就丢弃新解。然后回溯寻找下一个新解。

为此，我们先回顾一下回溯法的一般递归算法：

0-1背包问题的主程序

0-1背包问题的迭代实现

0-1背包问题的时间复杂性

显然0-1背包问题是一个求子集的问题。

求子集：从n个元素的集合S中找出满足某个性质子集。其搜索树称为子集树，是棵二叉树，通常有2n个叶结点，遍历的时间为O(2n) 。0-1背包问题的时间复杂性为O(2n)。

n后问题

要求在一个n×n的棋盘上放置n个皇后，使得她们彼此不受攻击。

按照国际象棋的规则，一个皇后可以攻击与之同一行或同一列或同一斜线上的任何棋子。

因此，N后问题等价于：要求在一个n×n的棋盘上放置n个皇后，使得任意两个皇后不得在同一行或同一列或同一斜线上。

八皇后问题

先建立一个8*8格的棋盘，在棋盘的第一行的任意位置安放第一只皇后。

紧接着，我们就来放第二行，第二行的安放就要受一些限制了，因为与第一行的皇后在同一列或同一对角线的位置上是不能安放皇后的，接下来是第三行，……，或许我们会遇到这种情况：在摆到某一行的时候，无论皇后摆放在什么位置，她都会被其它行的皇后吃掉，这时就必须要回溯，将前面的皇后重新摆放，

八皇后的一个可行解

八皇后问题的表示

设八个皇后为xi，分别在第i行(i=1，2，3，4……，8)；

问题的解状态：
可以用(1,x1)，(2,x2)，……，(8,x8)表示8个皇后的位置；
由于行号固定，可简单记为：(x1,x2,x3,x4,x5,x6,x7,x8)；

问题的解空间：(x1,x2,x3,x4,x5,x6,x7,x8)，1≤xi≤8(i=1，2，3，4……，8)，共88个状态；

约束条件：八个(1,x1),(2,x2) ,(3,x3),(4,x4) ,(5,x5), (6,x6) , (7,x7), (8,x8)不在同一行、同一列和同一对角线上。

原问题即：在解空间中寻找符合约束条件的解状态。

a 盲目的枚举算法

盲目的枚举算法
通过8重循环模拟搜索空间中的88个状态；
按枚举思想，以DFS的方式，从第1个皇后在第1列开始搜索，枚举出所有的“解状态”：

从中找出满足约束条件的“答案状态”。

约束条件：

不在同一列：xi≠xj；
不在同一主对角线上：xi-i ≠ xj-j；
不在同一负对角线上：xi+i ≠ xj+j。
违规的情况可以整合改写为：abs(xi - xj)=(abs( i-j )) or (xi = xj)

b加约束的枚举算法

如果能够排除那些没有前途的状态，会节约时间；

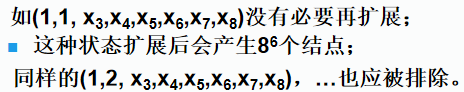
如何提前发现？在每一次扩展E结点后，都进行检查；

对检查结果如何处理？
检查合格的才继续向下扩展；遇到不合格的“掉头就走”。

此算法可读性很好，体现了“回溯”。但它只能解决八皇后问题，而不能解决任意的n皇后问题。

c递归回溯算法

d非递归回溯算法

没有递归因为k在控制

八皇后问题算法说明

八皇后问题中的核心代码：遍历过程函数；check函数。

解决此类问题的核心内容：
解空间树的搜索算法；
估值/判断函数：判断哪些状态适合继续扩展，或者作为答案状态。

n皇后问题

介绍过的方法：c递归回溯算法；d非递归回溯算法；

用递归回溯法求N后问题

求解N后问题中的数据表示

数组rec[n]表示棋盘。若rec[i]=j，1≤i, j≤n，表示棋盘的第i行第j列上有皇后。

数组C[j]=1表示第j列上无皇后，1≤j≤n

数组D[k]=1表示第k条下行(↘)对角线上无皇后。这里，k = i – j ， –n+1≤k≤n–1 。

例如：n=6;-n+1<=k<=n-1为-5<=k<=5

数组U[k] = 1表示第k条上行(↗)对角线上无皇后。

k = i + j ，2≤k≤2n 。

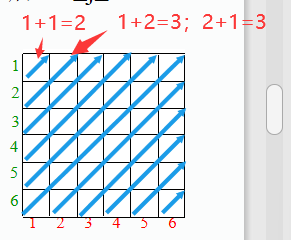
例如：n=6;2<=k<=2n为2<=k<=12

求解N后问题中的子程序

求解N后问题的主程序

N后问题的时间复杂性

时间上界为O(N!)

要精确估计N后问题的时间复杂度是一件很困难的事，但至少可以知道：它的约束条件比N个数的全排列更为严格，所有搜索的节点数肯定更少

课堂练习（没事可以做做）

最优装载问题

问题描述

有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi，且

装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有，找出一种装载方案。

贪心算法不能解决这个问题

回溯算法如何解决这个问题

容易证明，如果一个给定装载问题有解，则采用下面的策略可得到最优装载方案。
(1)首先将第一艘轮船尽可能装满
(2)将剩余的集装箱装上第二艘轮船
将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最接近。装载问题等价于以下特殊的0-1背包问题。

用回溯法设计解装载问题的O(2n)计算时间算法。在某些情况下该算法优于动态规划算法。

解空间：子集树
可行性约束函数(选择当前元素)：

上界函数(不选择当前元素)：
如果：当前载重量cw+剩余集装箱的重量r<=当前最优载重量bestw，那就继续
否则：当前载重量cw+剩余集装箱的重量r>当前最优载重量bestw,肯定不是最优解了，剪枝

构造最优解

为了构造最优解，必须在算法中记录与当前最优值相应的当前最优解。用x记录从根至当前结点的路径；bestx记录当前最优解。
算法搜索到叶结点处，就修正bestx的值。

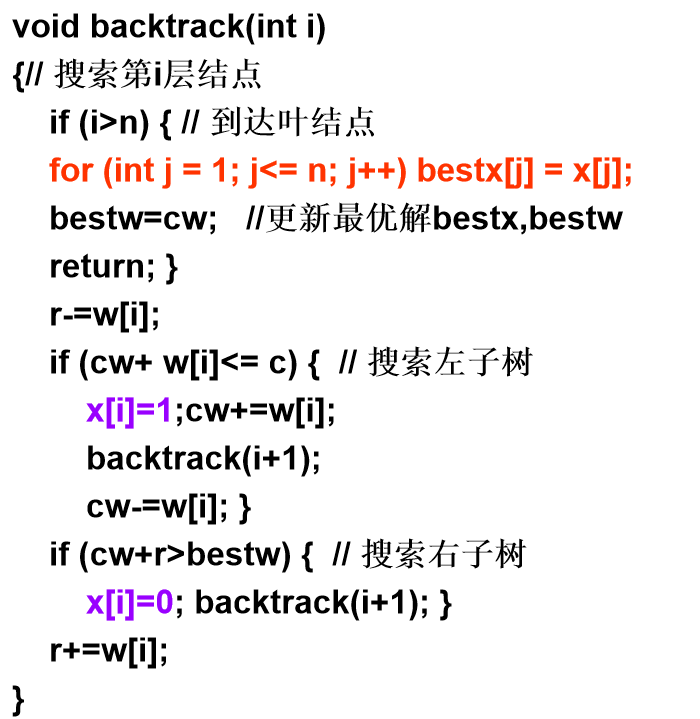
复杂度分析由于bestx可能被更新O(2n)次，改进后算法的计算时间复杂性为O(n2n)

旅行商问题

TSP：某售货员到若干城市去推销商品，已知各城市之间的路程(或旅费)。他要选定一条路线，经过每个城市一遍最后回到驻地的路线，使得总的路程(或总旅费)最小。

设G=(V, E)是一个带权图。图中各边的费用(权值)为正。图中一条周游路线是包括V中所有顶点的回路。一条周游路线的费用是该路线上所有边的费用之和。所谓旅行售货员问题就是要在图G中找出一条最小费用的周游路线。

数据结构

用数组C[n+1][n+1]存放n个城市间的费用值。

用数组P[n+1]记录已经找到的费用最小的周游路线，C为其相应的费用， C初值为∞。

用数组N[n+1]记录目前正在寻找的周游路线，NC为其相应的费用；

如果结点next不是N中已有的结点，且NC+C[N[s]][next]小于C，则结点next是可接受的。

如果NC+C[N[n]][1]小于C，则路线N更佳，于是P[] = N[]，C = NC+C[N[n]][1]。

TSP的递归程序Try

Try中的子程序

递归回溯求TSP的主程序

考虑TSP的迭代程序

为了便于迭代程序中回溯的判断，我们将城市结点编号为1 ~ n，用编号0作为末尾的标记。
采用末尾标记的迭代回溯法

TSP的迭代回溯

Backtrack中的子程序

迭代回溯求TSP的主程序

求解TSP的时间复杂性

显然TSP是一个求排列的问题。

求排列：确定n个元素的满足某种性质的排列。其搜索树称为排列树，通常有n!个叶结点，因此遍历排列树需要时间为O(n!)。

所以TSP问题的时间复杂性为O(n!)

求排列、求子集

求排列：确定n个元素的满足某种性质的排列。其搜索树称为排列树，通常有n!个叶结点，因此遍历排列树需要时间为O(n!)。

求子集：从n个元素的集合S中找出满足某个性质子集。其搜索树称为子集树，是棵二叉树，通常有2n个叶结点，遍历的时间为O(2n) 。

回溯法小结

回溯法是一种通用的算法，实为深度优先的搜索方法。

回溯法可以递归实现，也可以迭代实现。

回溯法通常求解两类问题：
(1)求排列：时间复杂性为O(f(n)n!)；
(2)求子集：时间复杂性为O(f(n)2n)；
这里f(n)为处理一个结点的时间复杂性。