数据结构第六章复习
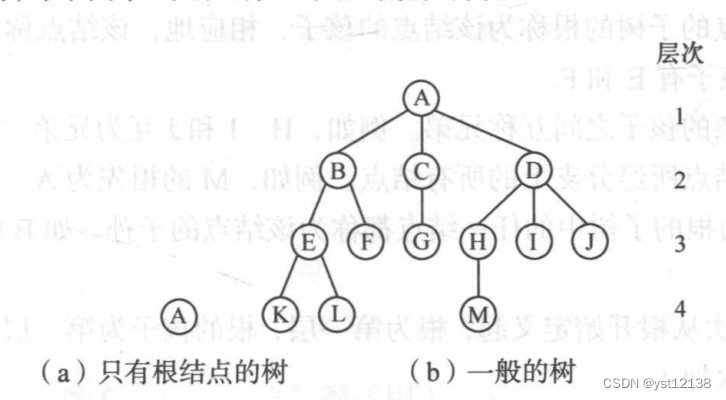
树的结构定义是一个递归的定义,现在树的定义中又用到树的概念。它的表示方法多样化,正说明了树的结构在日常生活中及计算机程序设计中的重要性。
一、概念:
度:
结点拥有的子树称为结点的度
叶子结点/终端结点:
度为0的结点称为叶子结点
孩子:
结点的子树的根称为该结点的孩子
兄弟:
同一个双亲的孩子
层次:
根为第一层,根的孩子为第二层
堂兄弟:
双亲在同一层的结点互为堂兄弟
深度:
树中结点的最大层次称为树的深度
二、二叉树
(1)定义
每个结点至多只有两颗子树
二叉树的五种基本形态:

(2)性质
1)在二叉树的第i层上至多有个结点
2)深度为k的二叉树至多有个结点
3)对任何一颗二叉树T,如果其终端结点为,度为2的结点数为
,则
? ? ?满二叉树:
,一颗深度为k且有个结点的二叉树称为满二叉树
4)具有n个结点的完全二叉树的深度为
5)对一颗有n个结点的完全二叉树对于任意结点有:
(1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则双亲PARENT(i)是结点
(2)如果2i>n,则结点i无左孩子(i为叶子结点);否则其做孩子是结点2i
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i-1
(3)二叉树的链式存储结构
1)定义:
在含有n个结点的二叉链表中有n+1个空链域
2)? ?二叉树的遍历:
遍历二叉树是按照某条搜索路径访问树中的每一个节点(仅访问一次),想要对二叉树进行操作首先得遍历。二叉树是由三个基本单元组成:根节点、左子树、右子树;则遍历二叉树的思路就是依次遍历左根右等6种不同的顺序,在此介绍三种:
先序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)访问根结点;
(2)先序遍历左子树;
(3)先序遍历右子树。
中序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)中序遍历左子树;
(2)访问根节点
(3)中序遍历右子树
后序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根节点
练习:
有如下题目:
1.已知:
先序遍历结果:A B D E C F
中序遍历结果:D B E A F C
请画出这颗二叉树:
解析:
- 从先序遍历结果中取出第一个节点作为根节点,这里是A。
- 在中序遍历结果中找到根节点A的位置,将中序遍历结果分成左子树和右子树两部分。左子树包含A左边的节点(DBE),右子树包含A右边的节点(FC)。
- 递归地对左子树和右子树进行步骤1和步骤2,直到子树为空。
答案:
A
/ \
B C
/ \ \
D E F2.已知:
先序遍历结果:A B C D E F G
中序遍历结果:C D B E A F G
解析:
- 从先序遍历结果中取出第一个节点作为根节点,这里是A。
- 在中序遍历结果中找到根节点A的位置,将中序遍历结果分成左子树和右子树两部分。左子树包含A左边的节点(CBDE),右子树包含A右边的节点(FG)。
- 递归地对左子树和右子树进行步骤1和步骤2,直到子树为空。
答案:
A
/ \
B F
/ \ \
C D G
/ \
E E三、树和森林
(1)树的存储结构
? ?1)双亲表示法
该方法以一组连续的存储单元存储树的结点,每个结点除了数据域data外,还附有一个parent域用以指示双亲结点在数组中的位置。
? ?2)孩子表示法
把每个结点的孩子结点排列起来,看成是一个线性表,且以单链表做存储结构,则n个结点有n个孩子链表(叶子的孩子链表为空表);而n个头指针又组成一个线性表,为了便于查找,可采用顺序存储结构。
3)孩子兄弟表示法
又称二叉树表示法,或二叉链表表示法,即以二叉链表做树的存储结构;链表中结点的两个链域分别指向该节点的第一个孩子结点和该结点的下一个兄弟结点,分别命名为firstchild域和nextsibling域。
树和森林
1)树与二叉树的转换(利用的就是把二叉树和树表示成相同的二叉链表)
2)森林与二叉树的转换
四、赫夫曼树
(1)定义
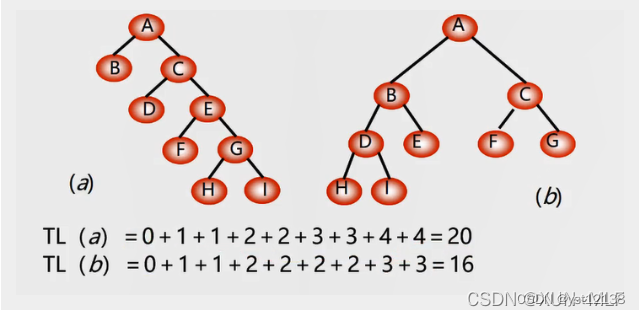
路径:从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度:路径上的分支数目称作路径长度。
树的路径长度:从树根到每一结点的路径长度之和。
权:将树中结点赋给一个有着某种含义的数值,则称这个数值称为该结点的权
结点的带权路径长度:从该结点到树根之间的路径长度与节点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和
哈夫曼树:又称作最优树;是带权路径长度最短的树(“带权路径长度最短”是在“度相同”的树中比较而得到的结果,因此有最优二叉树、最优三叉树等等)
特点:
? ? ? ? ?有2n-1个权值(结点)
? ? ? ? ?只有度为0或2的结点
注意:满二叉树不一定是哈夫曼树;在节点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树;注意区分树的路径长度和树的带权路径长度是完全不一样的
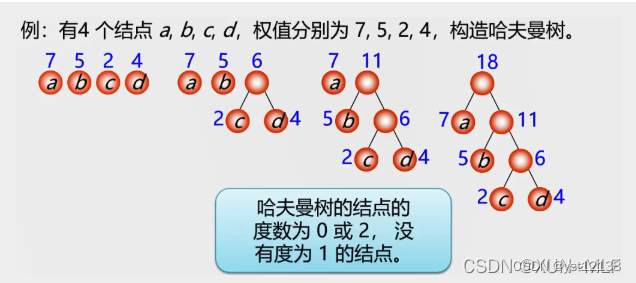
哈夫曼树的构造方法:
1.根据n个给定的权值{W1,W2,W3……Wn}构成n棵二叉树的森林,其中森林中的每一棵树都是一个根节点
2.在森林中选取两棵根结点的权值最小的成为左右子树,构造一棵新的二叉树,且设置新的二叉树的根节点的权值为其左右子树上根结点的权值之和。
3.在F中删除这两棵树,同时将新得到的二叉树加入森林中
4.重复第2步和第3步,直到森林中只有一棵树为止,这棵树即为哈夫曼树
图解:


(2)哈弗曼算法

-
在哈夫曼算法中,初始时有n棵二叉树,要经过n-1次合并最终形成哈夫曼树。
-
经过n-1此=次合并产生n-1个新结点,且这 n-1 个新结点都是具有两个孩子的分支结点
-
哈夫曼树中共有n+n-1 = 2n-1 个结点,且所有的分支结点的度都不为 1。
(3)译码
从根出发按照0或1找字符:左0右1
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!