构造LR(0)分析表和SLR(1)分析表
目录
1.构造LR(0)分析表
构造LR(0)分析表的步骤如下:
拓广文法--->列项目--->项目集规范簇--->分析表
拓广文法是一种用于描述上下文无关文法的元语法表示法,通过引入了一些扩展的符号和表示方式,以使得语法的描述更加直观
看下面的拓广文法,这里的(0)E'-->E:表示通过E'指向开始文法

列项目:
①首先将每个产生式的右部加“点”
②将通过不同符号的类列举出来
③若列举出来的语句中“点”后面是非终结符,那么需要将该非终结符所属的类都写下来,除了E'->E?。例如 E-->"点"E+T,"点"后面是E,所以将 E->"点" E +T 和 E-> "点" T 写下来,不写E'-->“点” E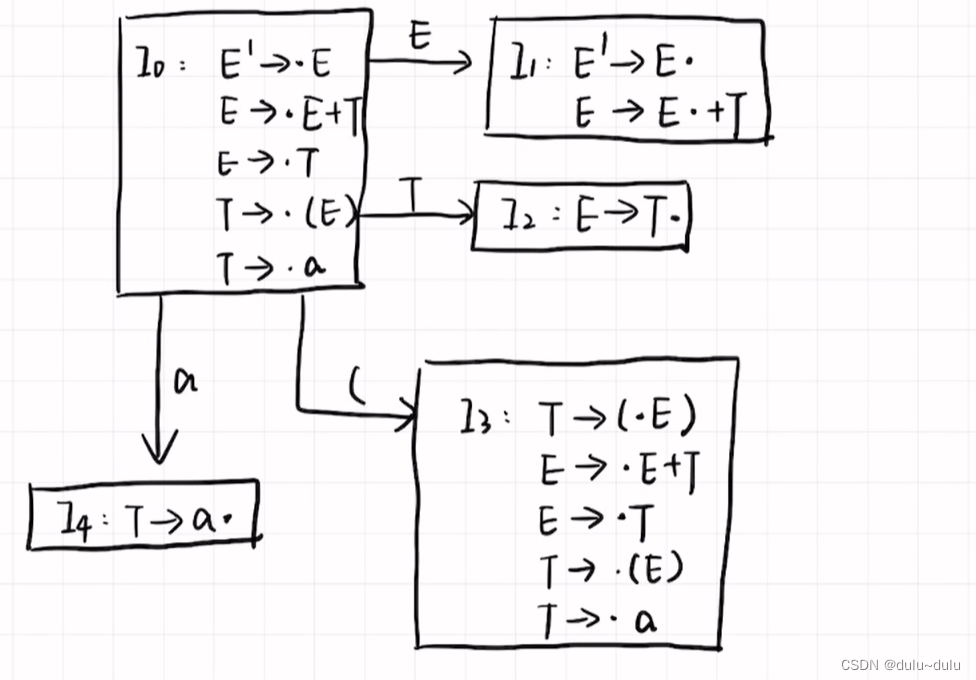
接下来分析I0:
由于E'--->E"点"中的"点"已经到最后了,不需要进一步分析
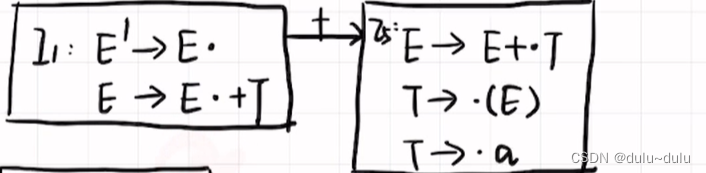
同理可得:
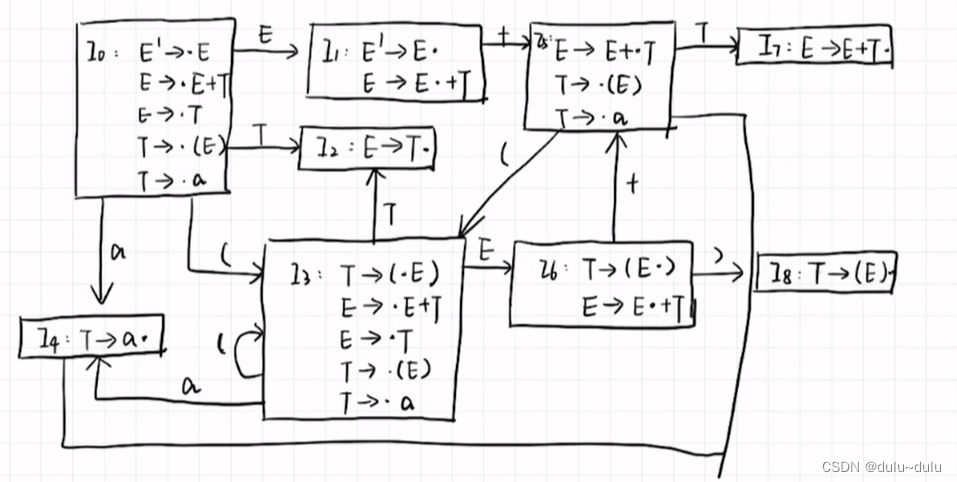
分析表:
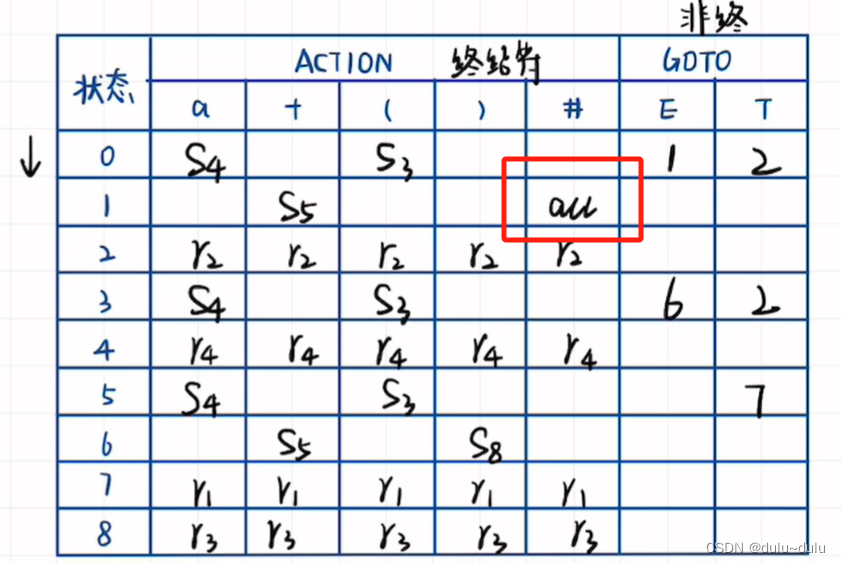
列出这样的表,0~8分别表示I0~I8:
第一行表示从I0出发,经过一个E,到达状态1,I0输入T,到达状态2,I0输入a,到达状态5,I0输入"(",到达状态3
以此类推:
若"点"已经在最后了, 表示这个项目已经结束,用”r“表示,在拓广文法中找到相同的项目,填入序号。例如这里的T2:E-->T,在拓广文法中对应(2)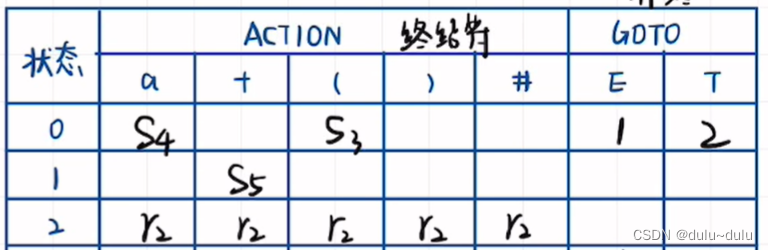
最后,状态1包含"E'-->E",所以在状态1的“#”列表明all
2.构造SLR(1)分析表
SLR(1)步骤和LR(0)相同,只是多求了一部FOLLOW集
点在不同位置,代表的项目不同:
归约项目(A-->
?):?在最后
移进项目(A-->?xB):?后面是终结符
接受项目(S--->
?):开始文法对应的
待约项目(A--->?XB):?后面是是非终结符
来看以下例子:
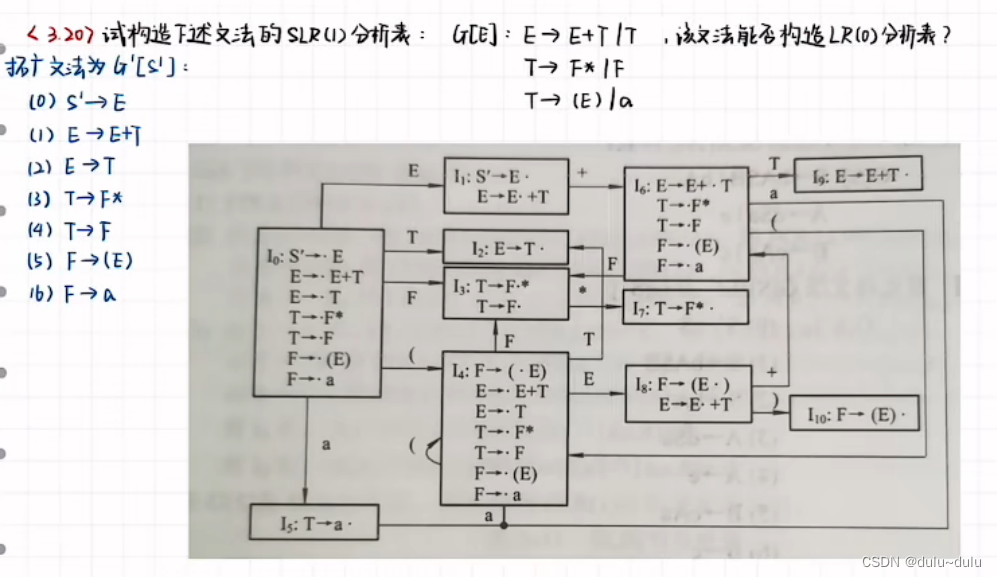
通过DFA得到的表如下图所示,但是这里先不用填“r”,表示终结
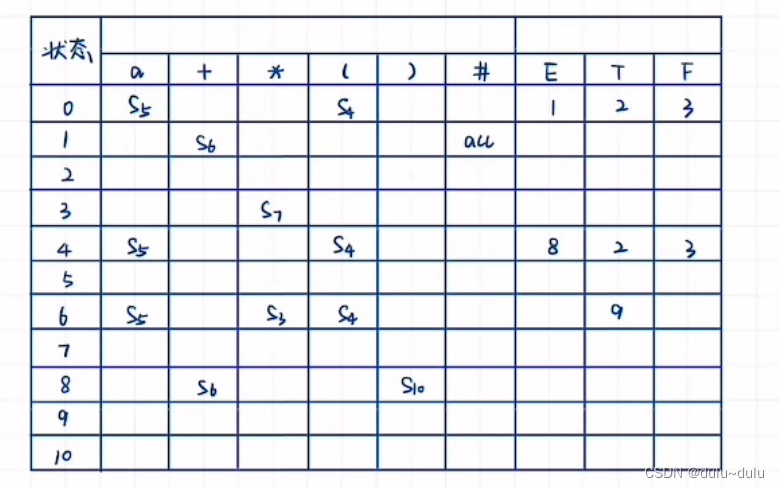
接下来我们求非终结符的FOLLOW集合:

将Follow集的终结符,写在"r"的位置,例如,拓广文法中(2)E-->T,那么E的FOLLOW集={+,),#}

以此类推,得到:
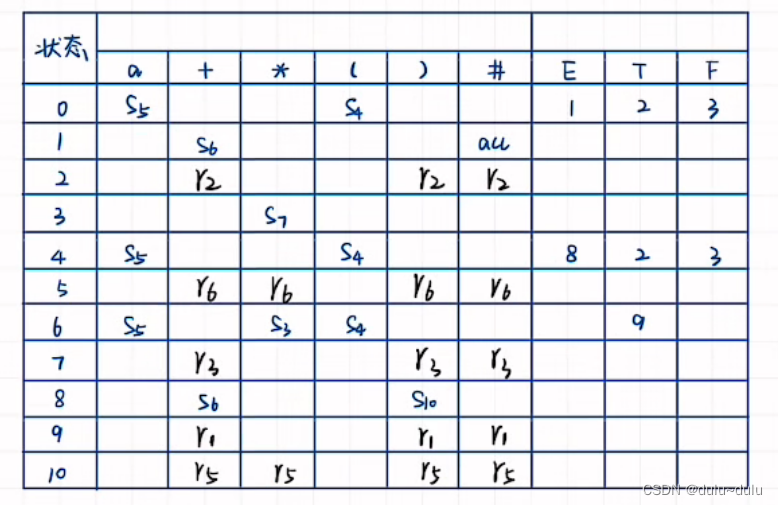
SLR(1)的出现其实是为了解决LR(0)的两个矛盾,即同一个项目中会产生矛盾:移进---归约????????归约---归约
(1)归约---归约
A--->a?
B--->a?
以上就出现了(归约---归约)错误,A的follow集/B的follow集不知是用"A--->a?"还是"B--->a?"
归约
(2)移进---归约(?后面是终结符---?在最后):
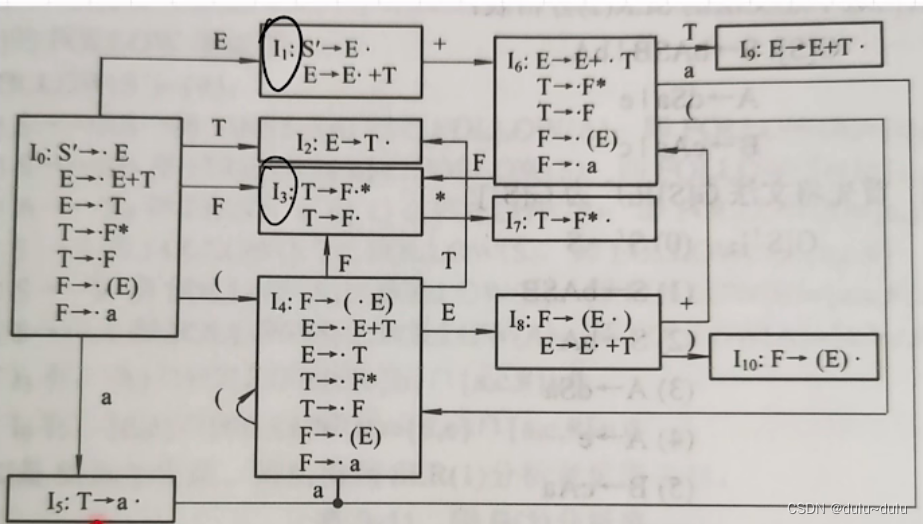
表中划圈部分满足,即I1和I3都存在移进---归约错误:
在I1中,我们将?后面的终结符“+”与该项目的开始符“ S’ ”的Follow集相交
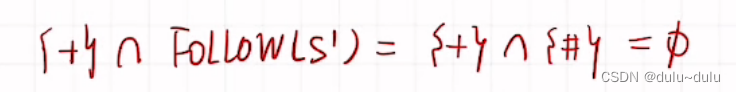
I3同理:
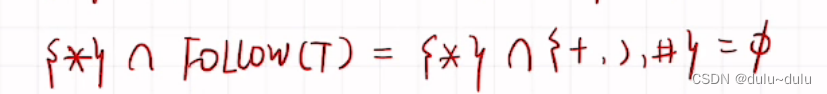
得出的两个交集皆为(空),那么说明LR(0)文法也满足SLR(1)文法的要求,是SLR(1)文法。
LR(0)和SLR(1)的联系
若不存在冲突项目,那么既是LR(0)文法,也是SLR(1)文法
若存在冲入项目,且满足Follow集为(空)的条件,那么就是SLR(1)文法,如果也不满足那么就既不是LR(0)文法,也不是SLR(1)文法
也就是说SLR(0)包含不冲突的项目,也包含符合条件的冲突项目:
SLR(0)LR(0)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 常用的gpt-4 prompt words收集
- 函数式编程 h函数
- Grafana增加仪表盘
- openwrt 搭建web
- JavaEE进阶(6)SpringBoot 配置文件(作用、格式、properties配置文件说明、yml配置文件说明、验证码案例)
- 微信小程序开发系列-03全局配置中的“window”和“tabBar”
- 5g/4g/北斗遥测终端机 水利遥测终端机
- 利用Pytorch预训练模型进行图像分类
- AI对决:ChatGPT与文心一言的深度比较
- java并发-ConcurrentHashMap 在Java7 和 8 的区别