ceres中lossfunction的选择

ceres中lossfunction的选择

在 Ceres Solver 中，核函数（或损失函数）用于处理优化问题中的异常值。核函数通过修改残差的贡献，降低异常值对总体优化结果的影响。两个常用的核函数是 Cauchy 核函数和 Trivial 损失函数，它们在处理异常值时有显著不同的行为：

Cauchy 核函数（Cauchy Loss Function）：

Cauchy 核函数是一种鲁棒的损失函数，特别适用于处理具有较大噪声的数据。它通过增加一个非线性的加权因子来降低异常值的影响，这个加权因子随着残差的增加而减少。Cauchy 核函数具有较长的“尾巴”，意味着即使残差很大，它对总体损失的贡献也会受到限制。这种函数在处理大量异常值时特别有用，因为它不会让任何单个观测值对总体结果产生过大影响。
其标准形式为：

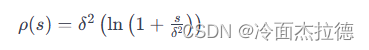
其中，s 是残差平方，而 δ 是核函数的参数，通常称为尺度参数（scale parameter）。在 Ceres Solver 中，柯西核函数的参数 δ 对优化过程有以下影响：

1.异常值的敏感性：尺度参数 δ 控制着对异常值的敏感度。较小的 δ 使得损失函数对于异常值更加敏感，导致异常值被更强烈地压缩。相反，较大的 δ 会减少对异常值的压缩，使得模型对这些值更加“宽容”。
2.收敛性质：参数的选择可能影响优化过程的收敛性。不适当的参数值可能导致优化过程不稳定或者收敛速度变慢。
3.解的偏差：适当的 δ 值可以帮助得到一个既对异常值有适当鲁棒性，又不会过度偏离真实数据分布的解。
4.平衡偏差与方差：选择合适的 δ 值有助于在偏差（bias）和方差（variance）之间达到平衡。较小的
5.δ 值可能导致高方差（即模型对数据的小变动过于敏感），而较大的 δ 值可能导致高偏差（即模型过于简化，不能充分捕捉数据的复杂性）。

Trivial 损失函数（Trivial Loss Function）：

Trivial 损失函数实际上是不应用任何额外处理的标准最小二乘损失函数。在这种情况下，所有的残差都会被平等对待，不论它们是正常值还是异常值。使用 Trivial 损失函数的优化等同于标准的最小二乘优化，没有任何鲁棒性对策。这种损失函数适用于那些数据质量较高，没有太多异常值的情况。

总结来说，Cauchy 核函数是一种鲁棒的损失函数，用于降低异常值的影响，而 Trivial 损失函数是最基本的形式，不对残差进行任何特殊处理。在选择适合的核函数时，需要根据数据的特点和优化问题的具体需求来决定。

添加lossfunction

	ceres::LossFunction* loss_function = nullptr;
	switch (loss_function_type) {//根据选择的核函数type
	case LossFunctionType::TRIVIAL:
		loss_function = new ceres::TrivialLoss();
		break;
	case LossFunctionType::SOFT_L1:
		loss_function = new ceres::SoftLOneLoss(loss_function_scale);
		break;
	case LossFunctionType::CAUCHY:
		loss_function = new ceres::CauchyLoss(loss_function_scale);
		break;