数据结构和算法-平衡二叉树（定义 插入 删除 时间复杂度）

发布时间：2023年12月21日

文章目录

平衡二叉树

总览

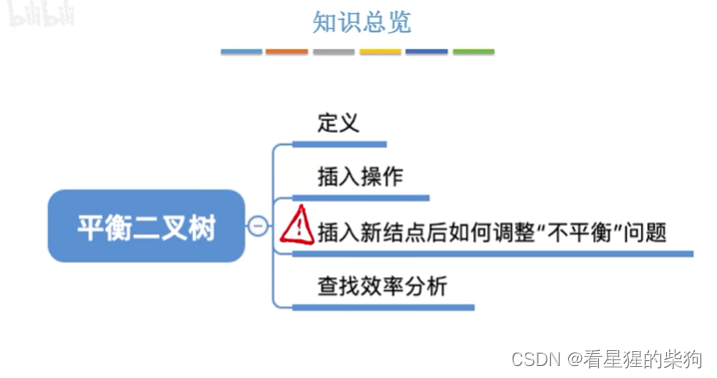
在这里插入图片描述

平衡二叉树的定义

保存平衡查找长度小些
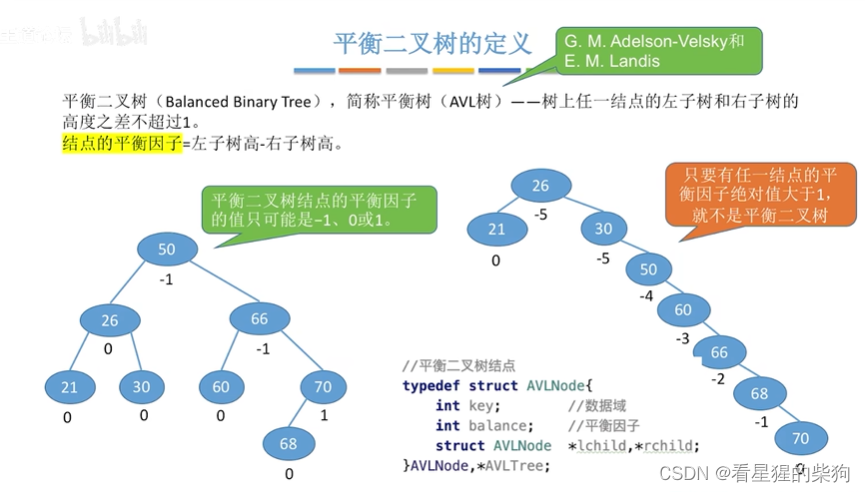
在这里插入图片描述

平衡二叉树的插入

插入后，再调整树使其恢复平衡。

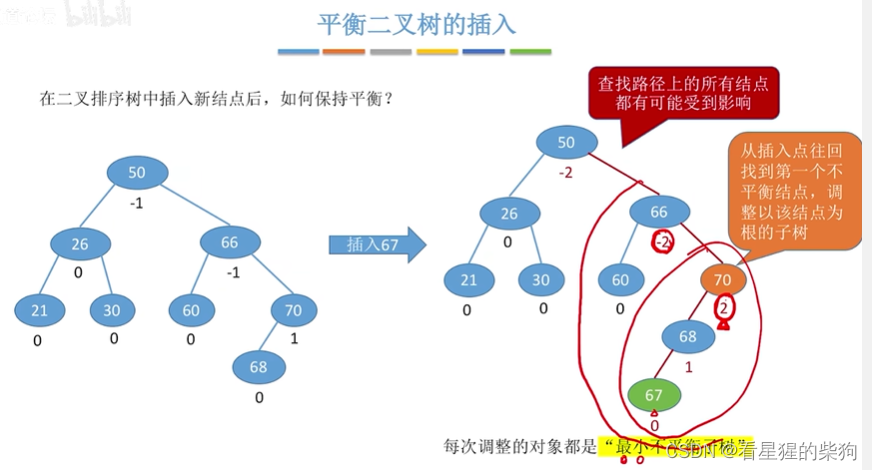
在这里插入图片描述
调整过后发现恢复平衡
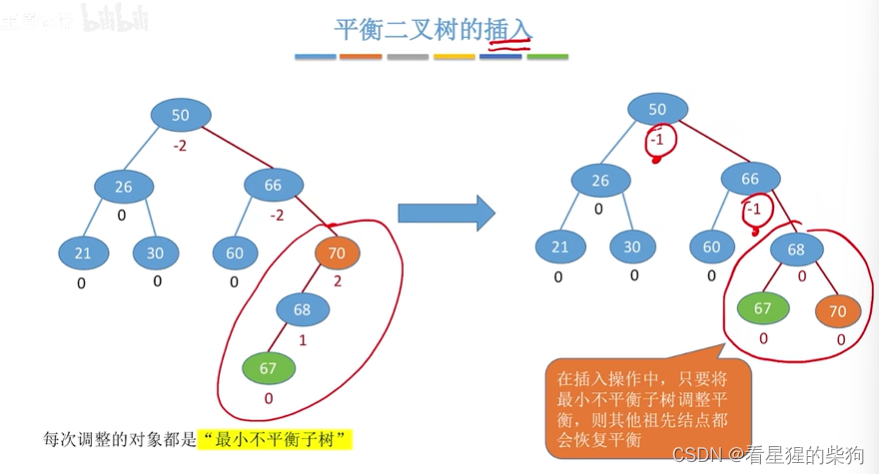
在这里插入图片描述

调整最小不平衡子树

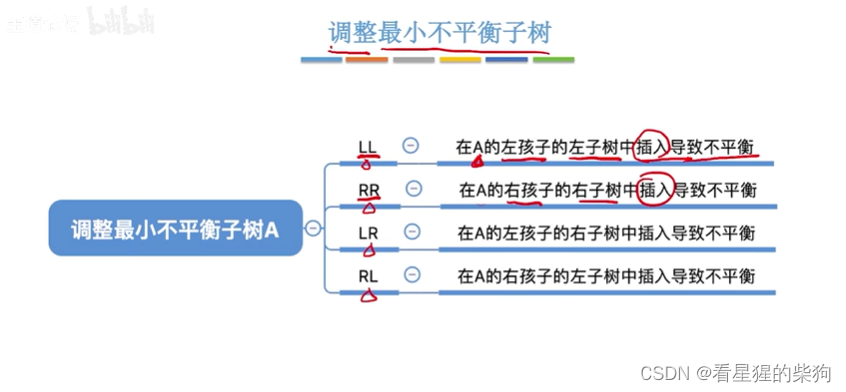
在这里插入图片描述
规律
左孩子右旋
右孩子左旋
在这里插入图片描述

在A的左孩子的左子树中插入导致不平衡

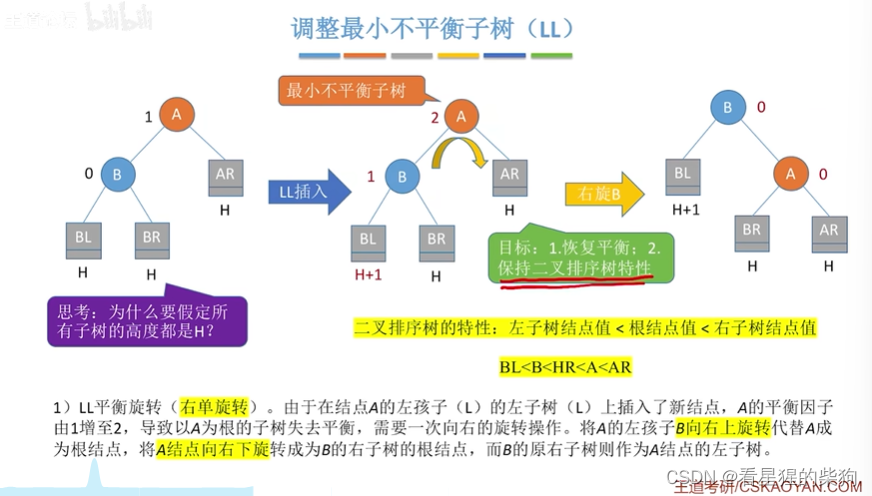
在这里插入图片描述
关于为什么所有子树的高度都是h是因为如果h+1或者h-1，那么插入后要不最小不平衡子树不是A，要不插入后没有最小不平衡子树，要不在插入前就已经出现最小不平衡子树了。总而言之都不满足假设的情况

在A的右孩子的右子树中插入导致不平衡

与上面的情况差不多，只不过改的位置不一样而已
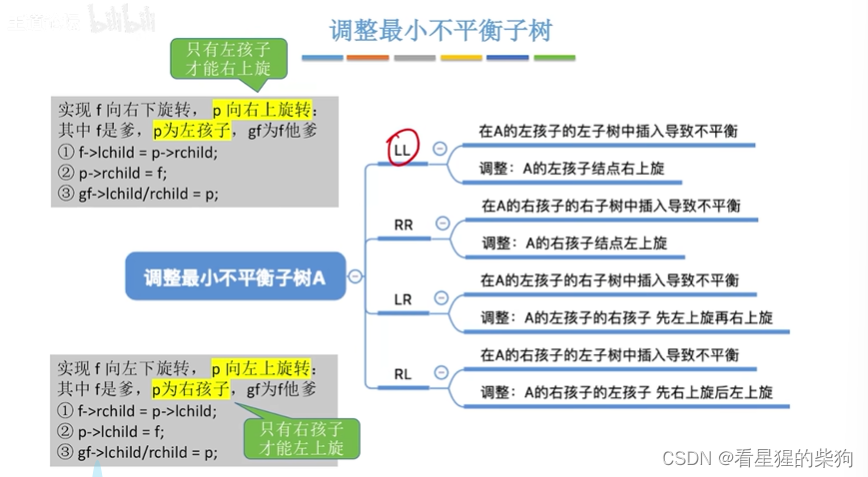
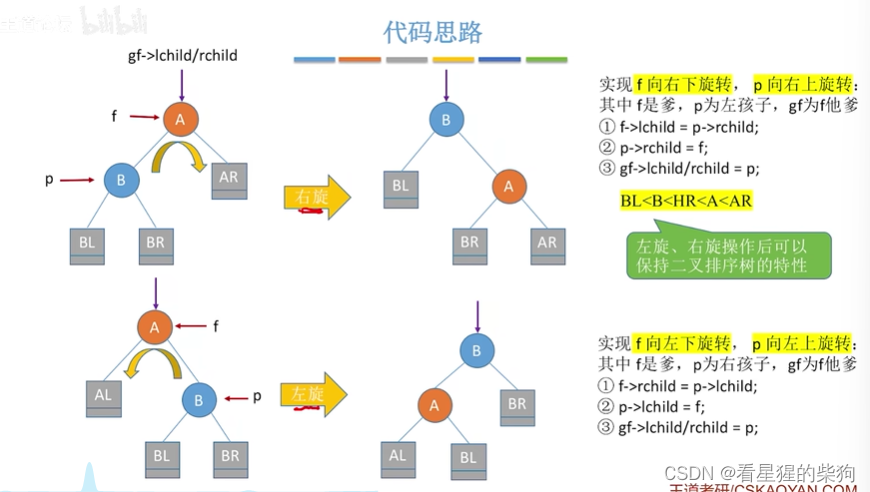
在这里插入图片描述

上述两种的代码思路

都是先更新A节点的子树为b的某个子树，然后再更新b的子树节点为f，最后再更新原来f的父节点中的子节点为b
在这里插入图片描述

在A的左孩子的右子树中插入导致不平衡

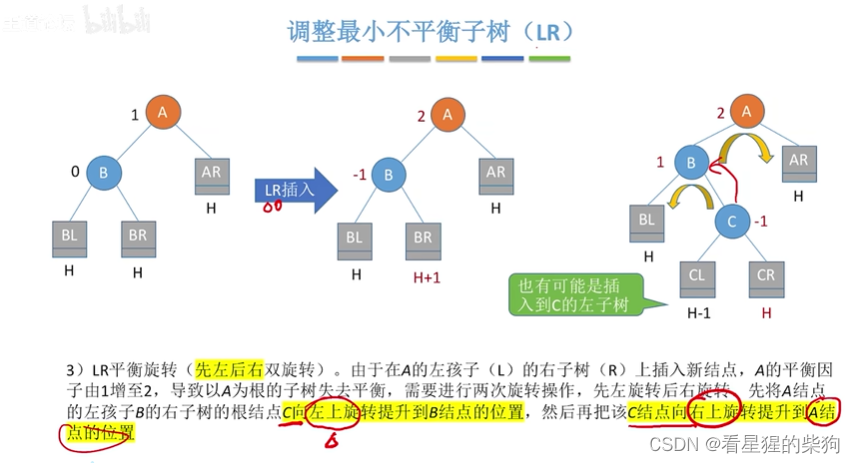
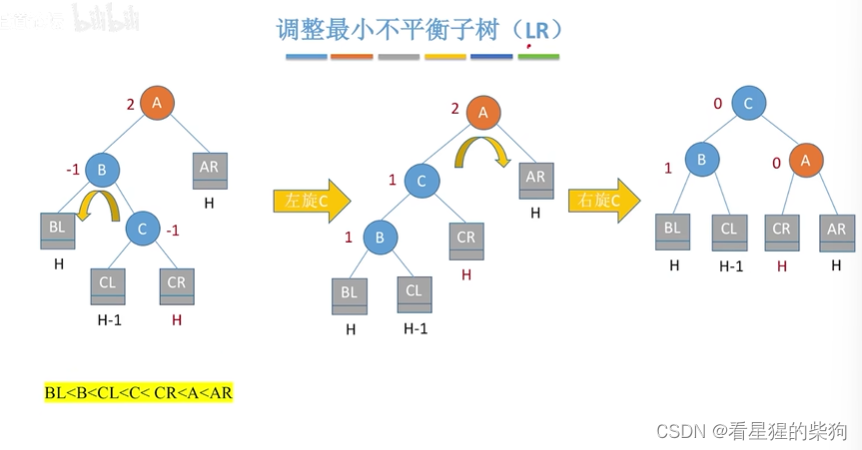
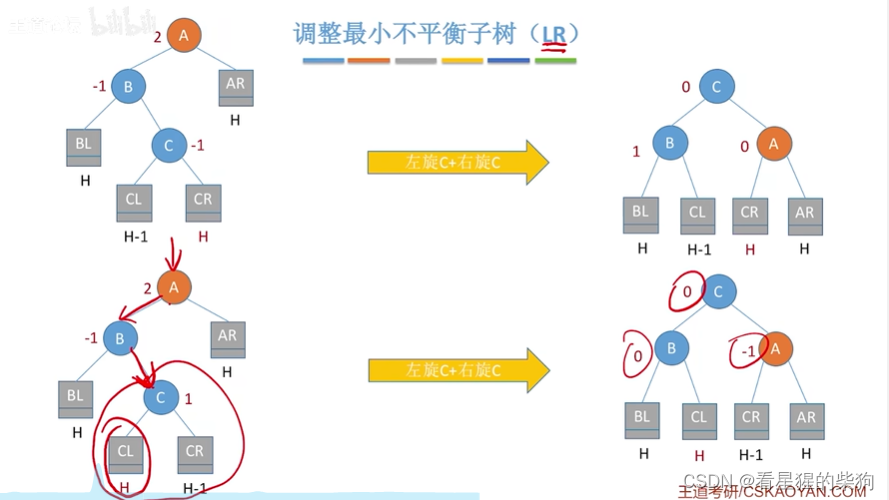
在这里插入图片描述
先左旋后右旋的结果
在这里插入图片描述
此时对应插入到c的左右子树两种情况
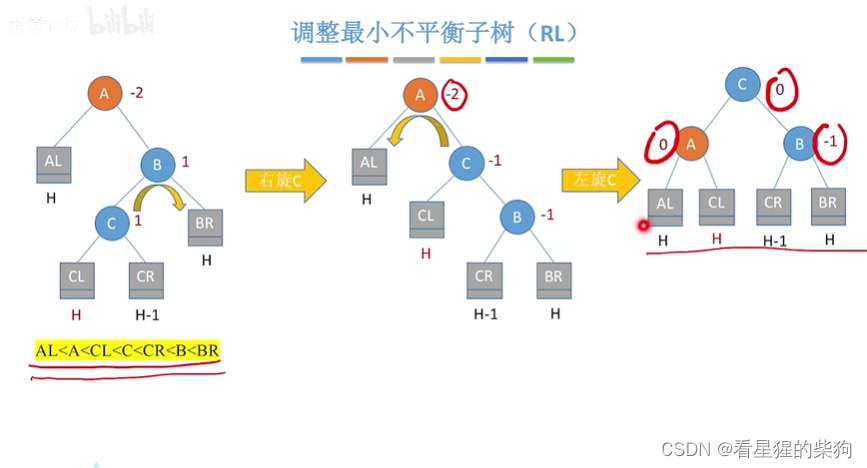
在这里插入图片描述

在A的右孩子的左子树中插入导致不平衡

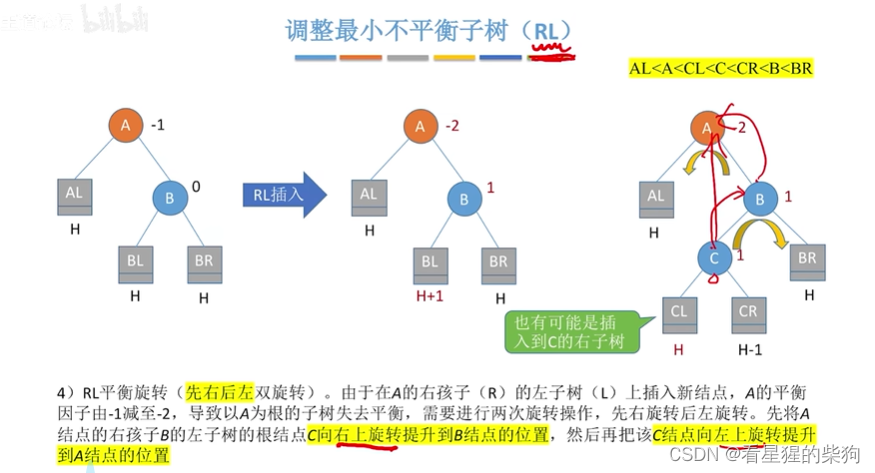
在这里插入图片描述
先右旋再左旋的过程
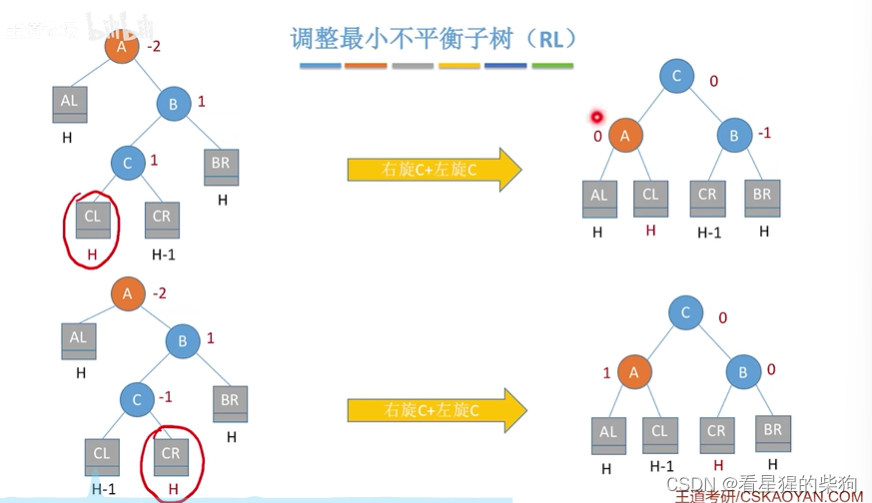
在这里插入图片描述
在这里插入图片描述

填个坑

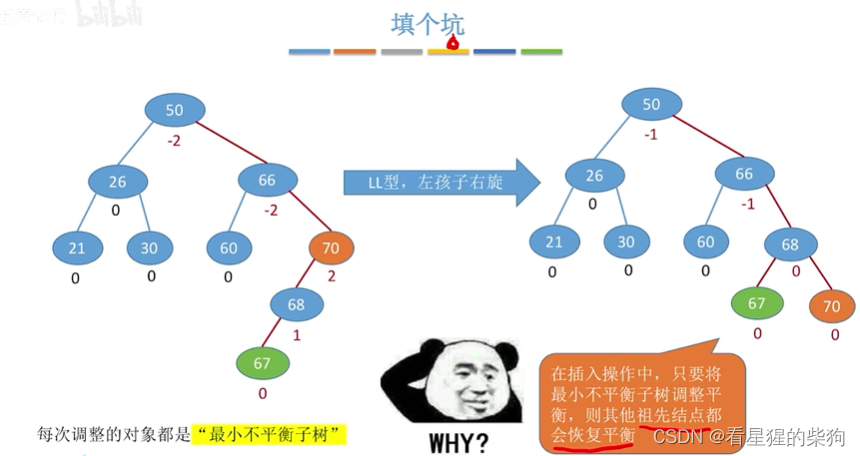
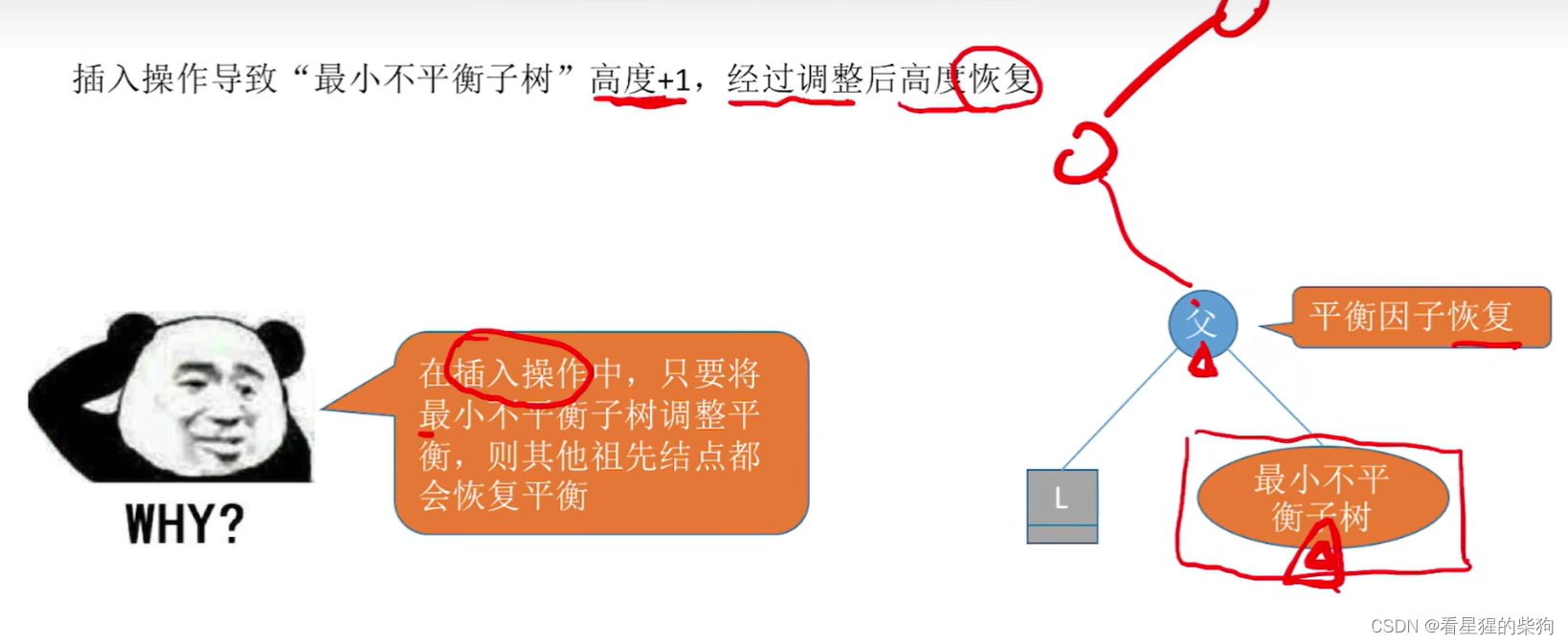
在这里插入图片描述
最小不平衡子树调整好后其父亲树都会调整平衡
在这里插入图片描述

练习

插入后，找到最小不平衡子树，让孩子旋转
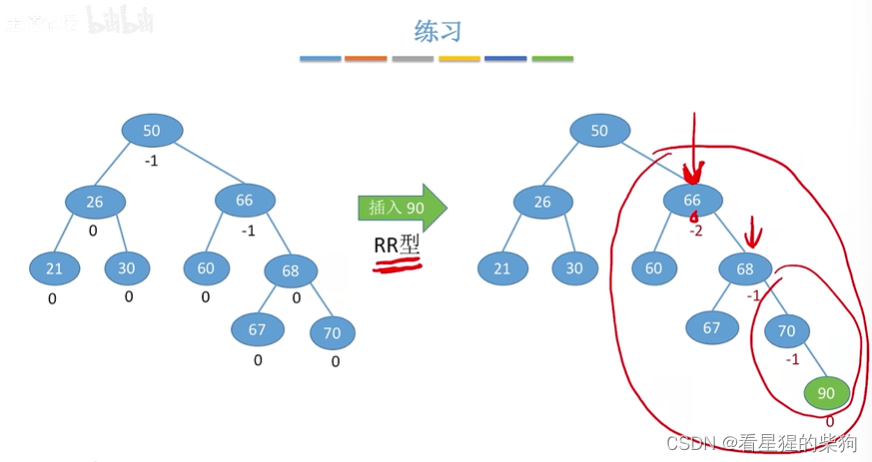
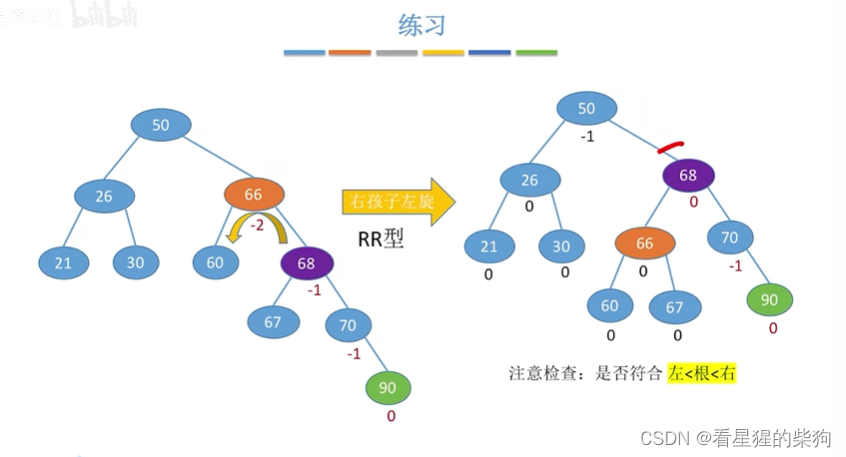
在这里插入图片描述

在这里插入图片描述
再插入
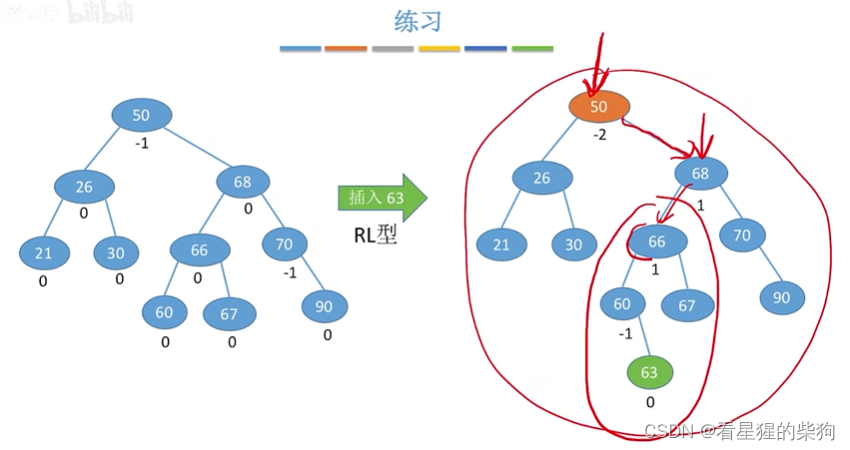
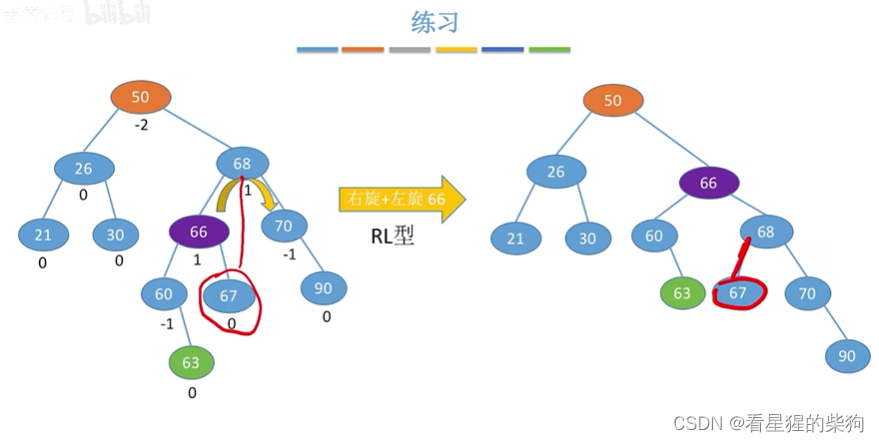
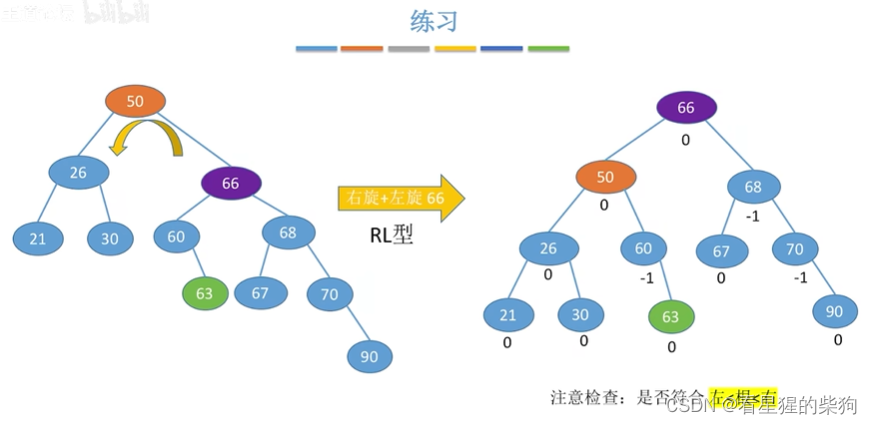
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
再插入
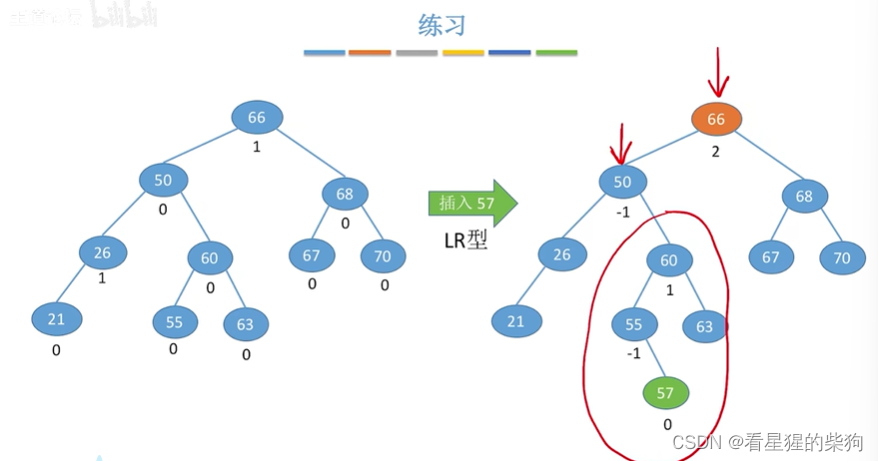
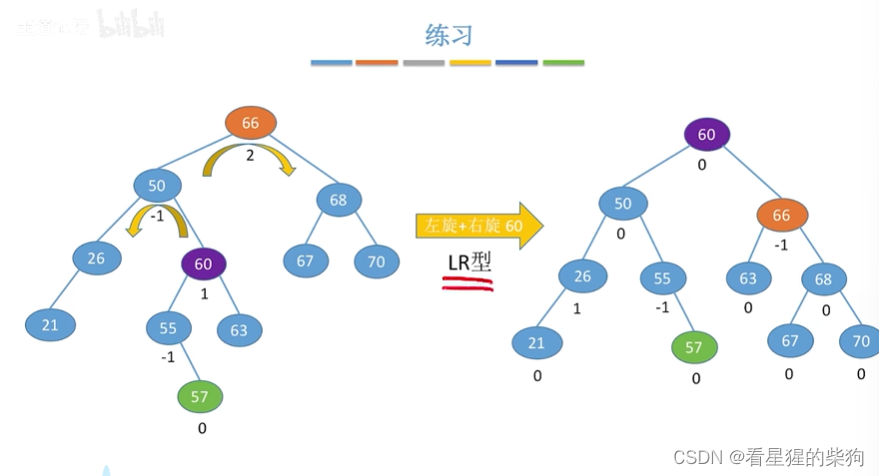
在这里插入图片描述
在这里插入图片描述

查找效率分析

由平衡二叉树可知道高度为h的平衡二叉树的节点最少的话是由一个根节点和两个子树构成，其中一颗子树为高度为h-1的最少节点数所构成的平衡二叉树，此时可以满足该树深度为h，而另一颗子树为高度为h-2的最少节点数所构成的平衡二叉树即可，若也为h-1的最少节点数所构成的平衡二叉树，那么此时没必要，节点相比与高度为h-2的最少节点数所构成的平衡二叉树多了，所以为h-2的即可
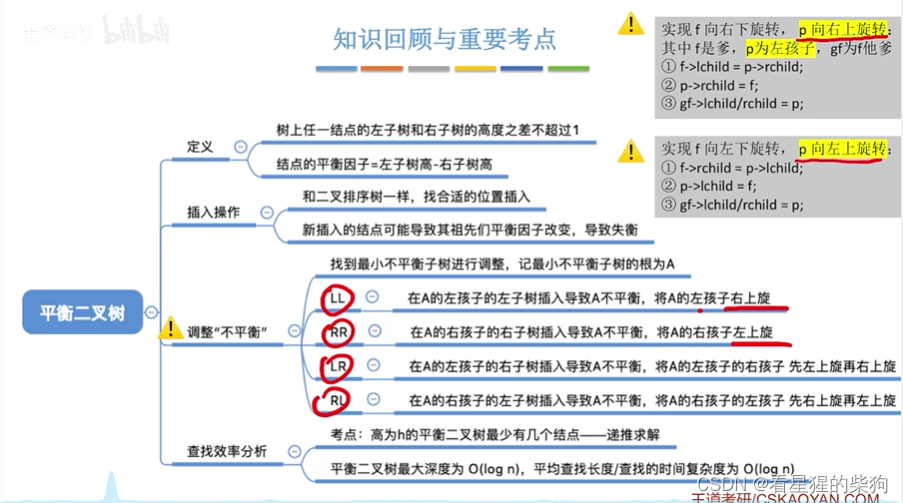
在这里插入图片描述

小结

在这里插入图片描述

平衡二叉树的删除

删除节点后，也要维持平衡二叉树的平衡

在这里插入图片描述

删除的节点是叶子-例1

在这里插入图片描述

在这里插入图片描述

删除的节点是叶子-例2

先删节点
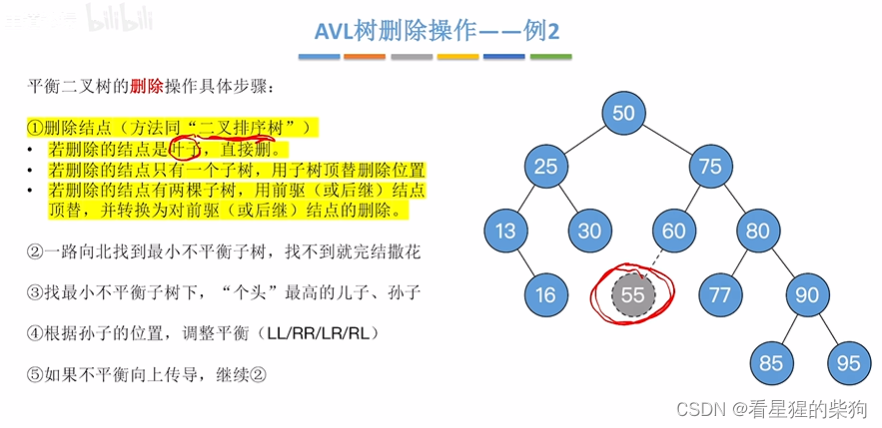
在这里插入图片描述
然后先上找到最小不平衡子树的根节点，同时找到该个头最高的儿子和孙子
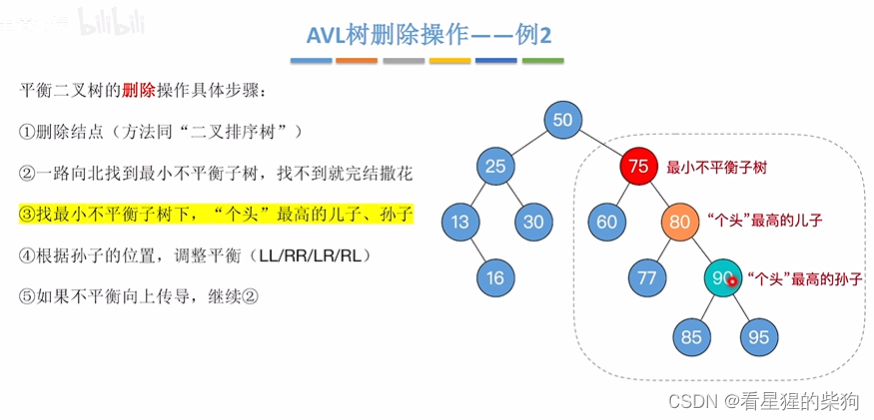
在这里插入图片描述
根据孙子位置，调整
此时80左旋
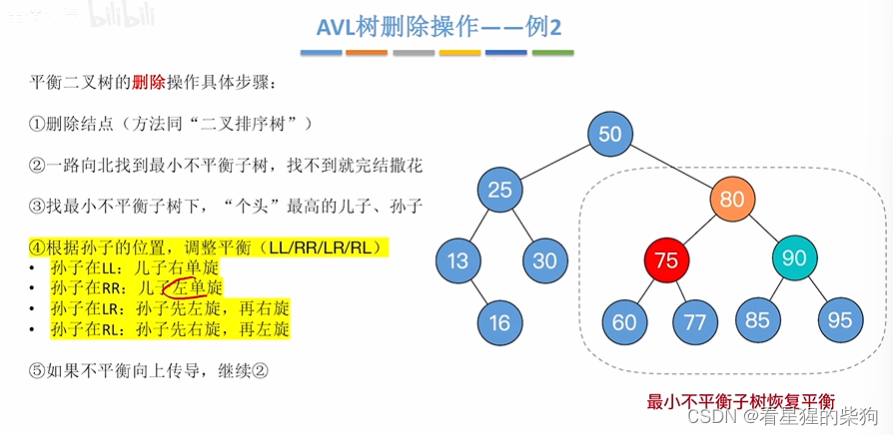
在这里插入图片描述

删除的节点是叶子-例3

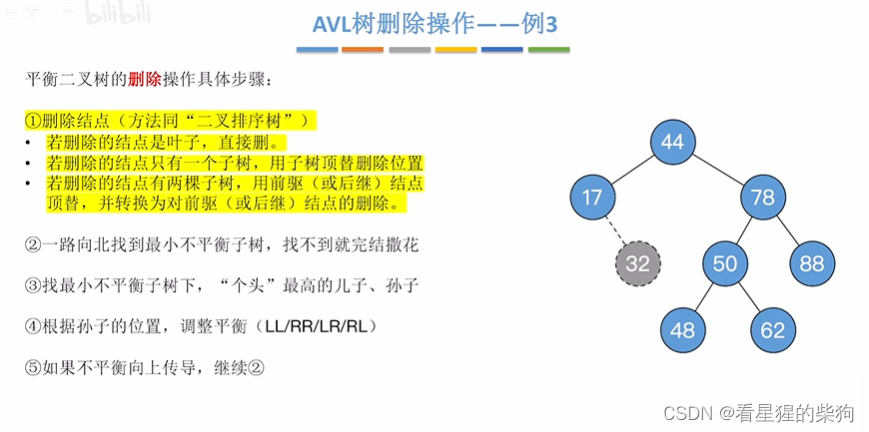
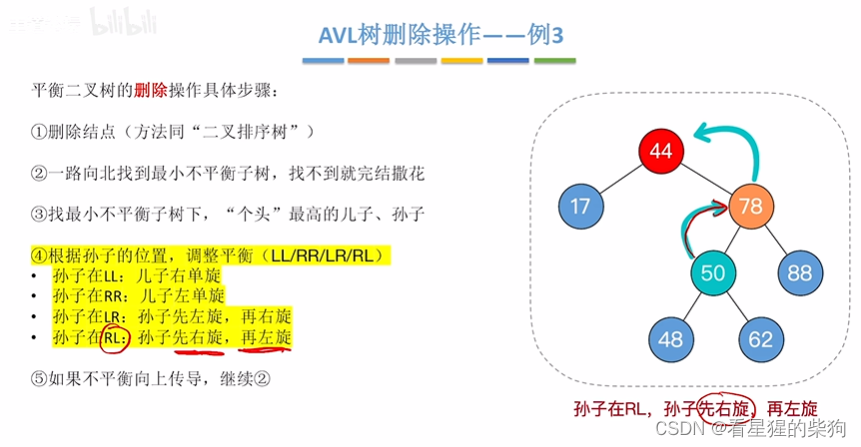
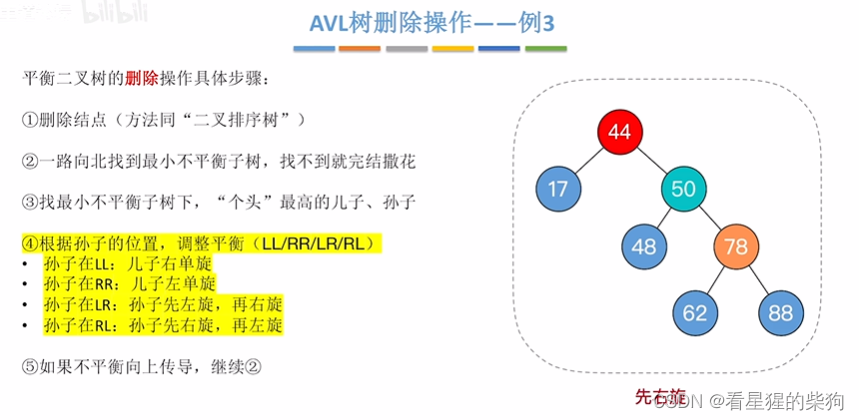
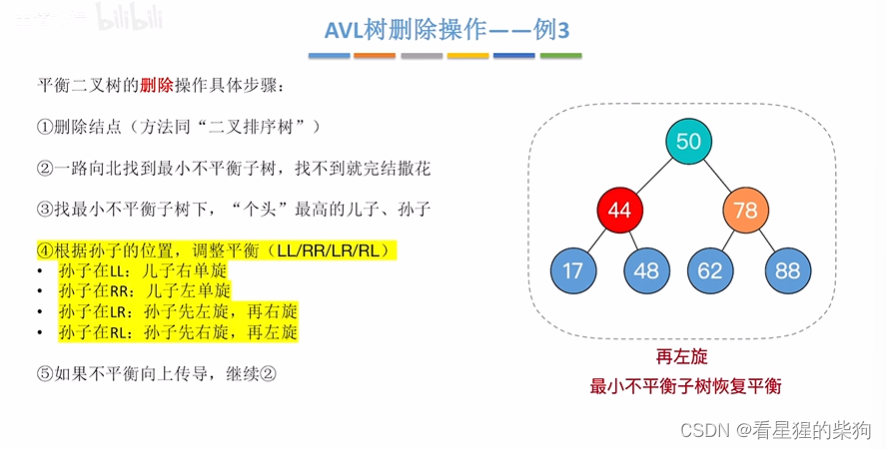
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

删除的节点是叶子-例4

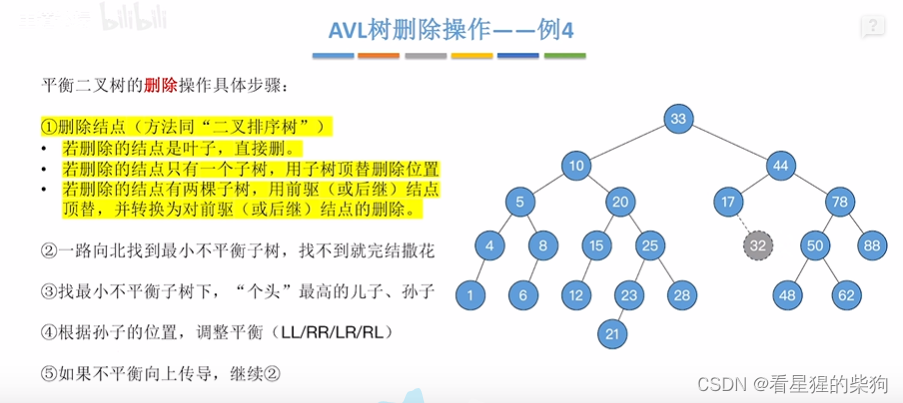
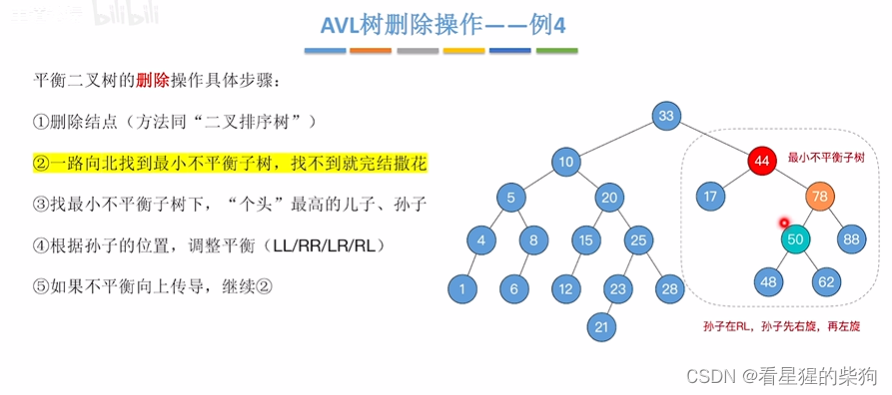
在这里插入图片描述
在这里插入图片描述
此时调整完后发现不平衡了，此时从调整后的子树继续向上传导，找到最小不平衡子树
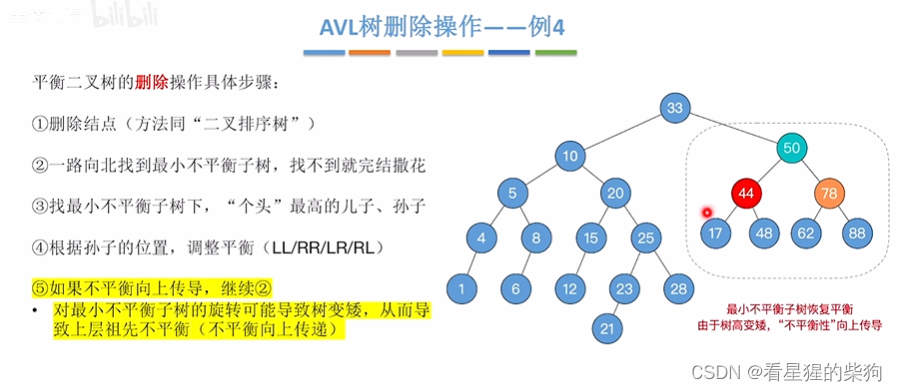
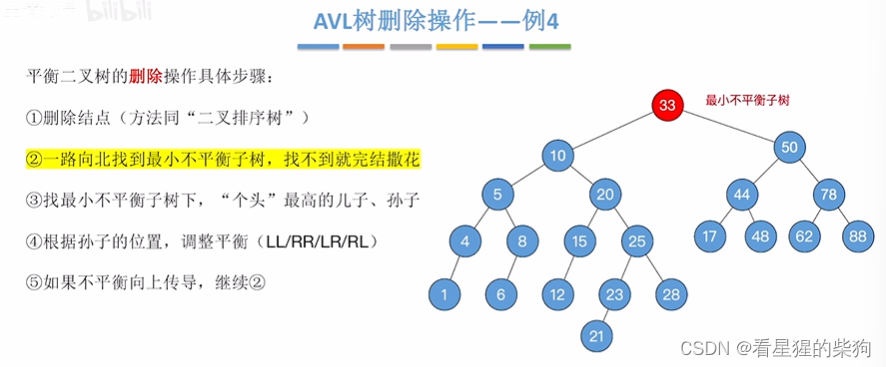
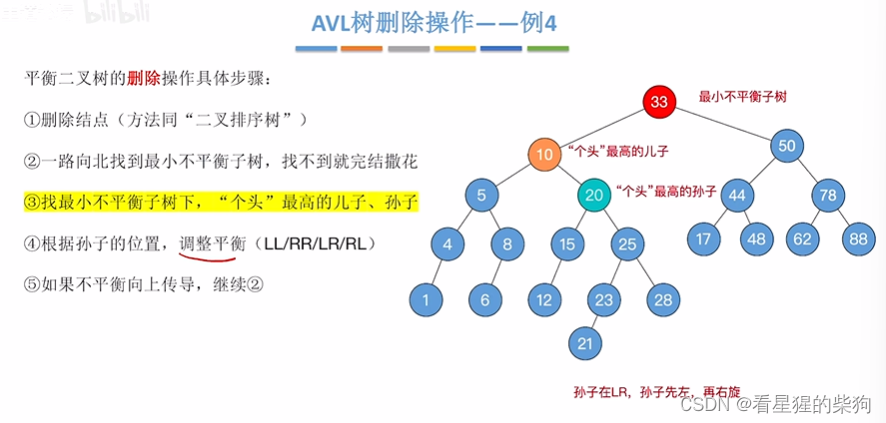
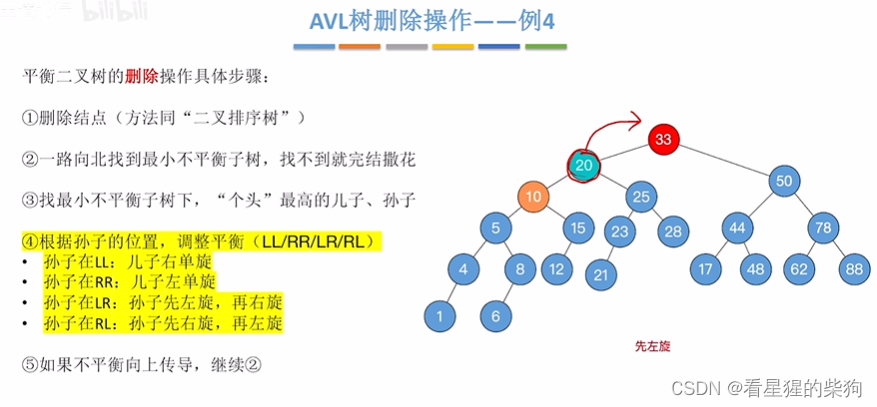
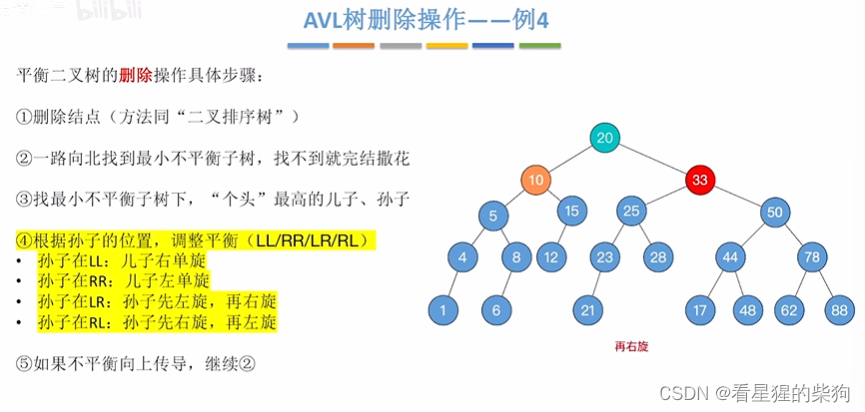
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
右旋后，不平衡特性没有向上传到了

删除的节点是有左右子树的-例5

两种顶替的策略
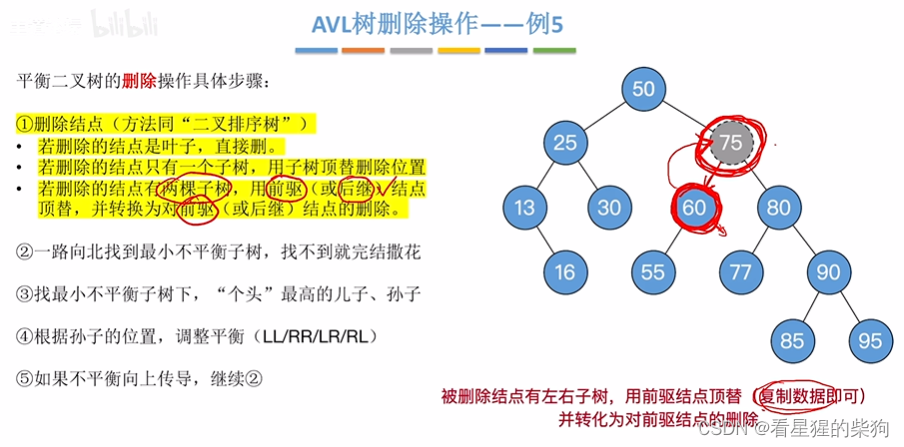
在这里插入图片描述
转换为删除的节点只有一个子树的类型
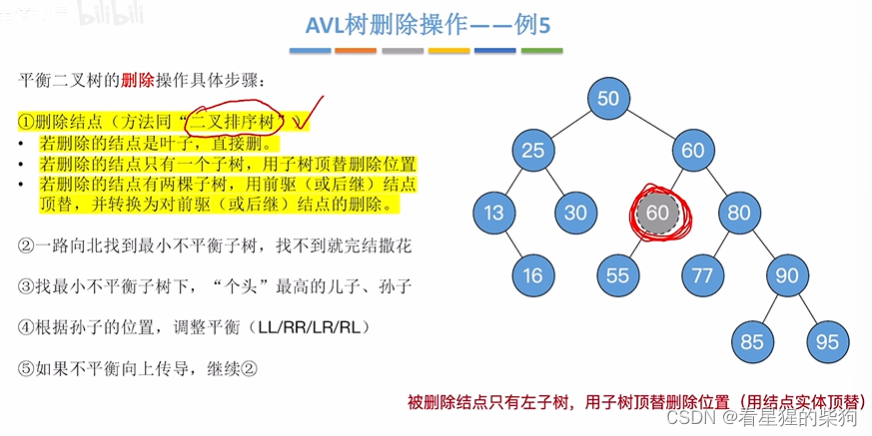
在这里插入图片描述
删除后
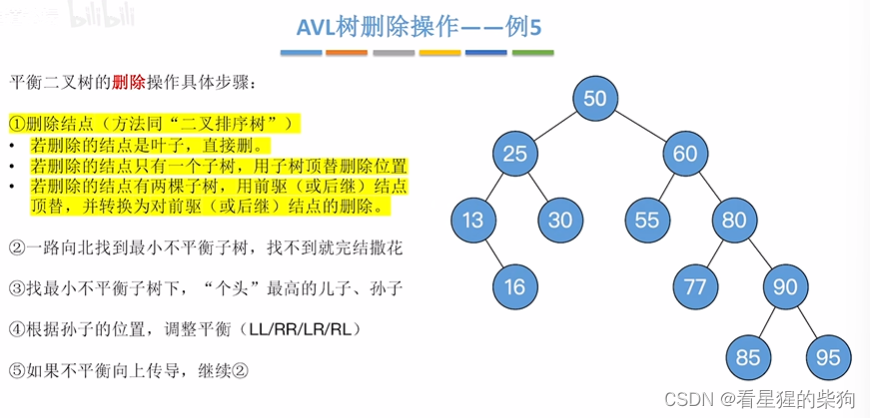
在这里插入图片描述
往上找最小不平衡子树，儿子左旋一次即可
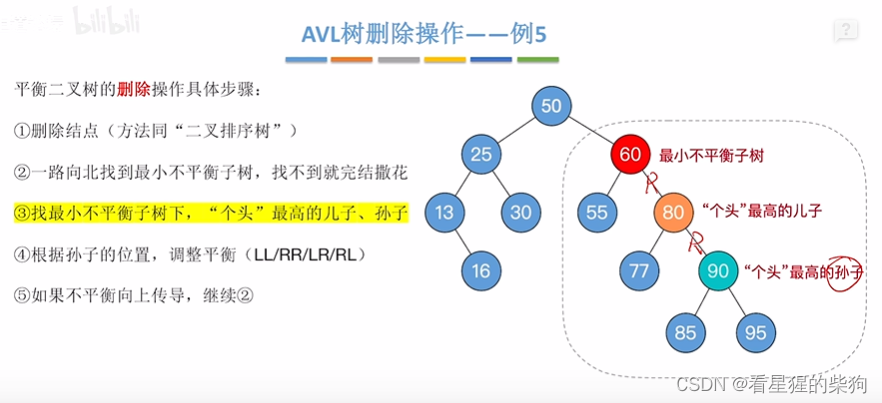
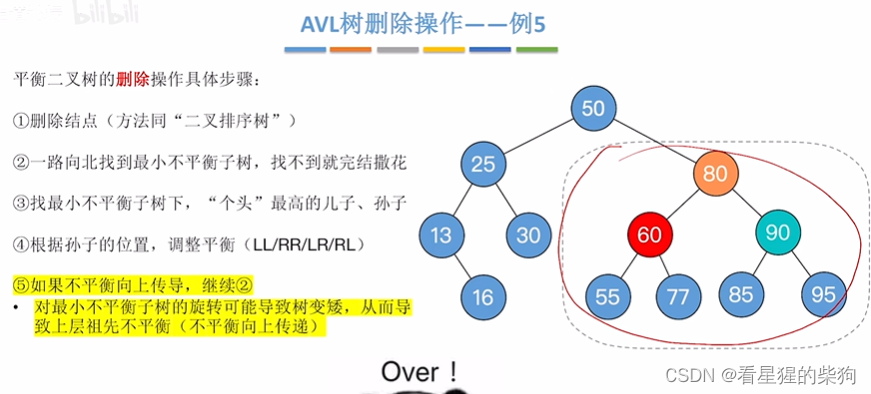
在这里插入图片描述
在这里插入图片描述
没有向上传导

删除的节点是有左右子树的-例6

此时用后继节点顶替
在这里插入图片描述
转换为删除叶子节点
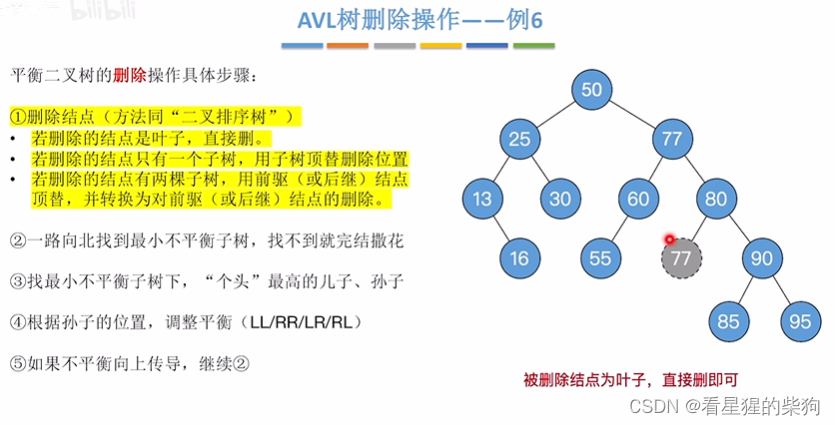
在这里插入图片描述
此时向北找到最小不平衡子树
此时孙子个头一样，所以选哪个作为个头最高的孙子
假设此时为右孙子为个头最高
此时儿子左旋一次即可
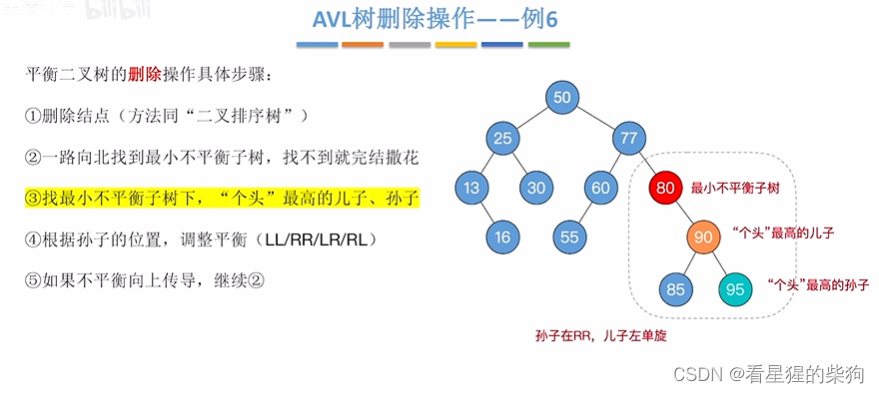
在这里插入图片描述
假设此时左孙子为个头最高

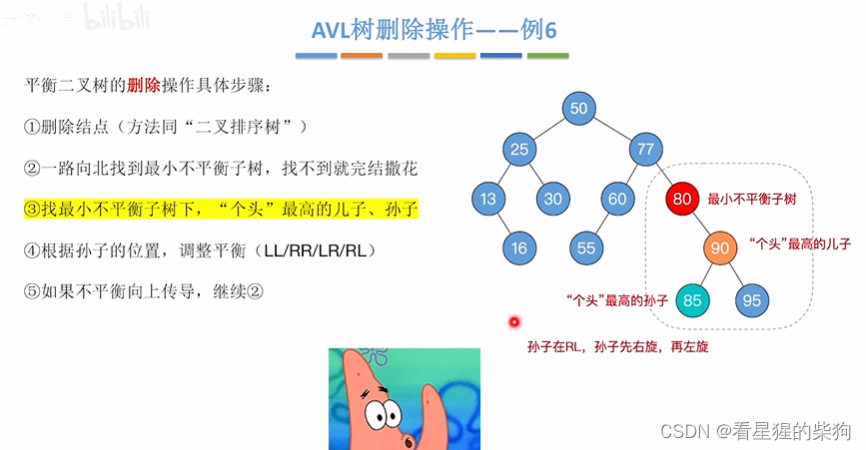
在这里插入图片描述
此时孙子先右旋
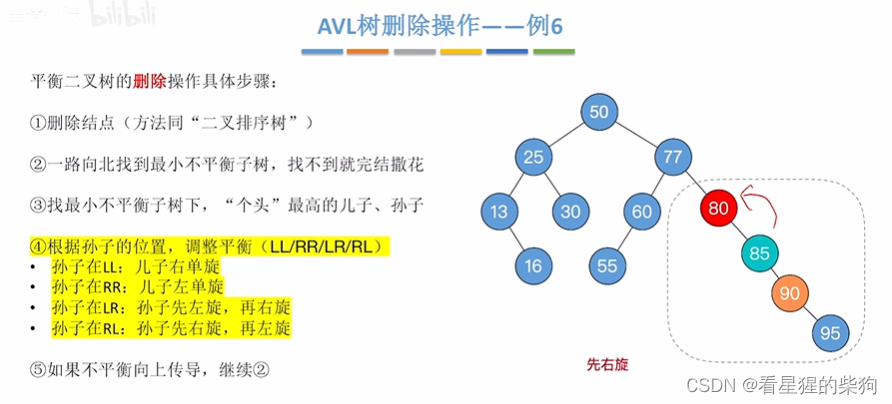
在这里插入图片描述
再左旋，此时不平衡无向上传导
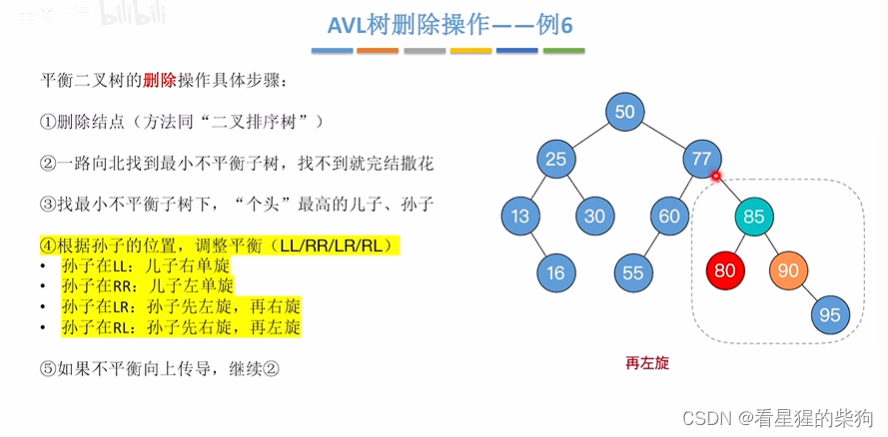
在这里插入图片描述

小结

旋转后子树变矮导致上层祖先不平衡
注意平衡二叉树删除操作的时间复杂度和插入的时间复杂度是一样的
在这里插入图片描述

文章来源:https://blog.csdn.net/llovewuzhengzi/article/details/135125393
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章