统计学R语言实验5 ：两个总体均值假设检验

统计学R语言实验5??两个总体均值假设检验

一、实验目的

1. 掌握理解两个总体均值假设检验的相关概念。

2. 掌握理解两个总体均值假设检验的相关方法。

3. 熟悉R语言等语言的集成开发环境。

二、实验分析与内容

完成教材P88的第7题、第8题。

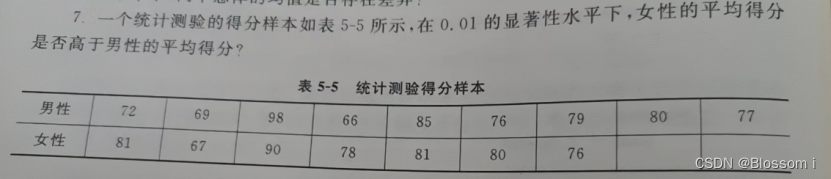
第7题有三种方法解题，如下：

（1）方法一：

假设方差不等

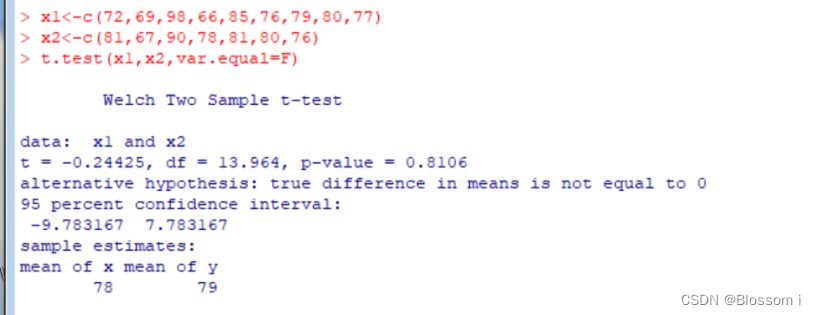
假设方差相等

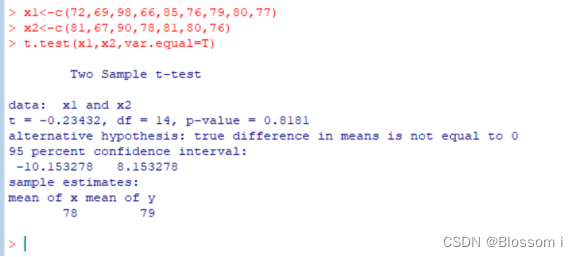
从上面两个运行结果来看，p值都大于0.01，则不能拒绝原假设，即认为女性和男性均值没有显著性区别。同时结果也给出了女性和男性样本数据的均值分别为：79和78。

（2）方法二：

（3）方法三:（方法二改进的，两个结果一样）

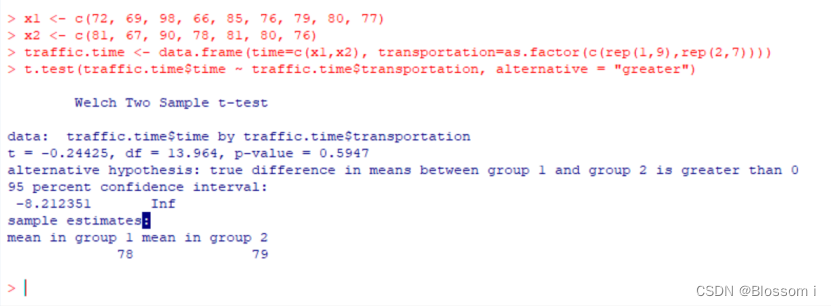
将两组数据x1和x2分别定义为男性得分和女性得分，并且认为测试时间单位为分钟。然后，我们将每个观测值对应的交通方式值存储在名为transportation的因子变量中。接下来，我们将时间和交通方式值存储在一个数据框中，命名为traffic.time。最后，我们使用t.test()函数执行了一个 Welch 独立两样本 t 检验，其中alternative = "greater"表示进行单侧测试，即测试女性的平均得分是否显著高于男性的平均得分。

根据方法二和三的结果，在 0.01 的显著性水平下不能拒绝女性平均得分与男性平均得分相等的原假设，因为P值为 0.5947，大于显著性水平0.01。因此，不能确定女性平均得分是否显著高于男性平均得分。

输入数据

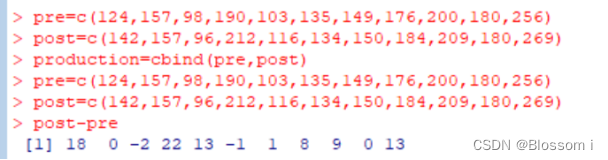
可以看出大部分是正数，相对于到校前的体重，大部分学生都再一年后重了。

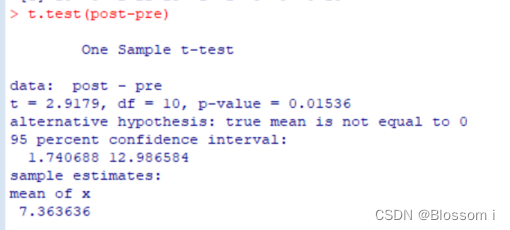
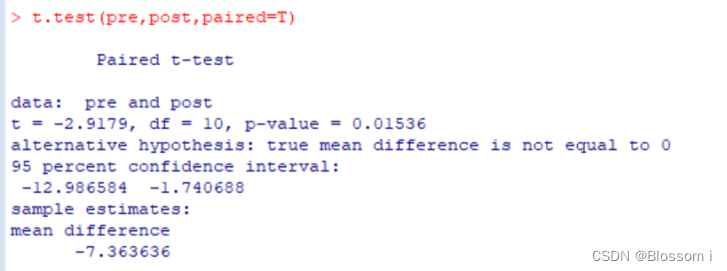
从结果来看，与配对t检验的t值-2.9179相比，看起来t统计量的绝对值明显变得更小了，p值都大于0.01，则不能拒绝原假设，即认为在0.01的水平下没有显著性区别。

三、实验总结

在本次实验中主要学习了两个总体均值假设检验的相关概念以及两个总体均值假设检验的相关方法，并继续加深对R语言等语言的集成开发环境的熟悉。在本次实验中，主要是根据样本数据对两个样本来自的两个独立总体的均值是否有显著差异进行判断。使用的前提条件：两个样本应该是相互独立的，样本来自的两个总体应该服从正态分布。首先要建立检验统计量，这个一般分两种情况，方差齐而未知；另外一种情况两总体方差不齐而未知。这两种情况计算统计量t的方法不同。所以在实际中应判断一下两独立总体的样本方差是否相等，并选择不同的方法来判断。然后计算检验统计量的观测值和p值，最后在给定的显著性水平上做出判断决策。