LC 2807. 在链表中插入最大公约数

2807. 在链表中插入最大公约数

难度 ： 中等

题目大意：

给你一个链表的头 head ，每个结点包含一个整数值。

在相邻结点之间，请你插入一个新的结点，结点值为这两个相邻结点值的 最大公约数 。

请你返回插入之后的链表。

两个数的 最大公约数 是可以被两个数字整除的最大正整数。

提示：

• 链表中结点数目在 [1, 5000] 之间。
• 1 <= Node.val <= 1000

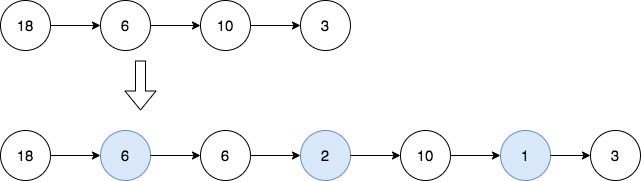
输入：head = [18,6,10,3]
输出：[18,6,6,2,10,1,3]

递归实现

难点在于代码的实现，怎么求最小公倍数

最小公倍数的模板

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    int gcd(int a, int b)  {
        return b ? gcd(b, a % b) : a;
    }
    ListNode* insertGreatestCommonDivisors(ListNode* head) {
        function<void(ListNode*)> dfs = [&](ListNode* u) -> void {
            if (!u->next) return;
            dfs(u->next);
            ListNode* newNode = new ListNode(gcd(u->val, u->next->val));
            newNode->next = u->next;
            u->next = newNode;
        };  
        dfs(head);
        return head;
    }
};

时间复杂度 $O(n)$

结束了