文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《基于8760小时生产模拟的离网风光储氢系统规划方法》

本专栏栏目提供文章与程序复现思路，具体已有的论文与论文源程序可翻阅本博主免费的专栏栏目《论文与完整程序》

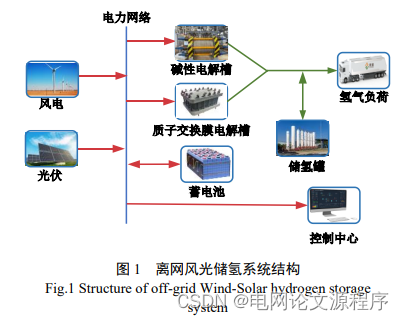
这篇文章的标题指的是一种离网（off-grid）风光储氢系统规划方法，该方法基于对全年 8760 小时的生产模拟。以下是对标题中的关键术语和概念的解读：

1. 离网系统（Off-grid system）： 这指的是不依赖传统电力网络的系统。离网系统通常是独立的，通过本地资源满足能源需求，而不依赖于主电网。

2. 风光储氢系统（Wind-solar-hydrogen system）： 这是一种整合了风能、太阳能和氢能技术的系统。风能和太阳能用于电力生成，而多余的电力则被用来产生氢气，从而实现能源的储存。

3. 8760 小时生产模拟（8760 hours production simulation）： 这表示在模拟中考虑了一整年的时间，每小时都进行了生产和能源系统的模拟。这种方法能够提供对系统在不同季节、天气条件和时间段的性能的全面了解。

4. 规划方法（Planning Method）： 这是指在文章中介绍的一种系统设计和优化方法。在这个上下文中，规划方法可能涉及到确定系统的组件、容量、运行策略等，以最大程度地满足离网系统的能源需求。

因此，整体而言，这篇文章可能详细阐述了一种通过对整年 8760 小时的生产情况进行模拟来规划离网风光储氢系统的方法。这样的方法可以帮助设计者更好地了解系统在不同情景下的性能，并做出更科学的决策，以提高系统的可靠性和效率。

摘要：风光可再生能源制氢是符合我国“双碳”目标、促进绿色工业发展的重要技术路径，建设离网风光储氢工业园区，能够有效实现可再生能源的就地消纳，降低电网建设压力。现有制氢园区规划中广泛采用基于典型日或典型场景的规划方法，在缺乏大电网支撑的离网园区规划中对全年风光波动与生产模拟结果表征存在偏差，而基于全年8760小时进行生产模拟则引入海量变量与约束，模型求解困难。因此，该文针对离网风光储氢园区规划方法展开研究，提出基于8760小时生产模拟的规划模型，并通过模型转化与改进Benders分解实现模型求解。首先，基于不同电制氢设备与储能设备模型，建立离网风光储氢系统的运行规划一体化模型。进一步，对上层规划主问题引入公共运行变量，对运行层子问题进行逐月拆分，降低单一子问题模型维度，并基于Benders分解法对模型进行求解。最后，通过山东海化地区实际算例，验证所提离网风光储氢系统规划方法能够实现基于8760小时生产模拟的设备容量规划，相比基于典型日与典型场景规划方法，能够降低园区全生命周期成本，实现更低的单位制氢成本。

这段摘要讨论了风光可再生能源制氢作为符合中国“双碳”目标和促进绿色工业发展的重要技术路径。文章提出了建设离网风光储氢工业园区的概念，旨在有效实现可再生能源的本地利用，从而减轻电网建设的压力。

具体来说，摘要中指出了目前制氢园区规划中普遍采用的基于典型日或典型场景的规划方法在离网园区中存在一些问题。这是因为这些方法在缺乏大电网支持的离网环境下，无法准确反映全年风光波动与生产模拟结果，存在一定的偏差。相比之下，基于全年 8760 小时进行生产模拟虽然更全面，但也引入了海量的变量和约束，使模型的求解变得复杂。

为解决这一问题，研究提出了基于8760小时生产模拟的规划模型，并采用Benders分解法进行模型求解。该方法首先建立了离网风光储氢系统的运行规划一体化模型，考虑了不同的电制氢设备与储能设备模型。随后，通过引入公共运行变量，对运行层子问题进行逐月拆分，从而降低了单一子问题模型的维度，有助于提高求解效率。

最后，通过在山东海化地区进行的实际算例验证，研究表明所提出的离网风光储氢系统规划方法能够实现基于8760小时生产模拟的设备容量规划。相较于基于典型日与典型场景规划方法，这种方法能够降低园区全生命周期成本，实现更低的单位制氢成本。这意味着提出的方法在实践中具有潜在的经济和环保优势。

关键词： 离网制氢;风光储氢;容量配置;生产模拟;

1. 离网制氢（Off-grid Hydrogen Production）:

   • 涉及在没有依赖于大电网的条件下进行制氢的过程。这可能涉及在偏远地区或无法接入传统电力网络的地方进行制氢。

2. 风光储氢（Wind-Solar Hydrogen Storage）:

   • 表示使用风力和太阳能等风光可再生能源来进行制氢，并将制得的氢气进行储存。这可能涉及将可再生能源直接转化为氢气以供后续使用。

3. 容量配置（Capacity Planning）:

   • 指规划和配置系统中不同组件的容量，这里可能是指制氢系统中各种设备（如电制氢设备、储能设备）的容量安排。

4. 生产模拟（Production Simulation）:

   • 涉及使用模型或仿真工具来模拟生产过程，特别是在这种情况下，是对制氢过程进行全年 8760 小时的模拟，以更全面地了解系统的性能和变化。

综合而言，这些关键词指向一项研究，其目标是在离网条件下，利用风光可再生能源进行氢气生产，并通过容量配置和生产模拟来优化系统设计，以实现更经济和环保的氢气生产。这可能对满足中国的“双碳”目标和推动绿色工业发展具有重要意义。

仿真算例：

算例数据采用山东海化地区历史实际 8760 小 时风光资源及负荷数据，系统配置方案中包含风光 储氢系统中两类制氢设备、风电机组、光伏 、电/ 氢两类储能设备等典型设备类型，单位功率风光机 组 8760 小时出力标幺值曲线如图 3 所示，全年制 氢总产量目标为5000万标方，售氢价格为35元/kg， 园区厂用电基础负荷为 500kW。特别的，由于制氢 园区氢气输入负荷受实际氢气用途影响，可能存在 绿氨、冶金、氢燃料、成品氢气运输等多种场景， 本文重点关注制氢园区能源系统侧配置方案，因此 以签订售氢合同为例，制氢负荷约束满足全年总产 量目标，且为单日产量不低于计划产量的 70%。算例验证计算平台配置为 Intel(R) Core(TM) i5-8400 CPU，8.00G RAM，基于 Matlab2022a 仿真 平台建模，主问题与分解子问题调用 Gurobi 商用求 解器进行求解。 受现有制氢设备发展水平限制，通常 AWE 与 PEM 单台制氢设备容量小于 5MW，为满足全年制 氢目标，规划结果中将包含 10 台及以上制氢设备， 8760 小时生产模拟下的变量与约束数量超过求解 器求解能力，因此通过直接划分上层规划模型与下 层运行模型并调用求解器求解的方法无法实现。 因此，为验证本文所提规划模型与求解方法， 在本节中，将验证所提求解方法的可行性，并与现 有主流方法进行对比。共设置三种方案进行对比， 分别为： 方案 1：本文提出的基于 8760 小时生产模拟的规划求解方法； 方案 2：根据风光资源分布，将全年分为夏季、 冬季、过渡季三种典型日，在双层规划模型中基于 典型日进行生产模拟； 方案 3：基于风光资源特点，采用 K-means 聚 类生成 4 种典型场景，在双层规划模型中基于典型 场景进行生产模拟。

仿真程序复现思路：

复现该仿真涉及以下步骤：

1. 数据准备： 使用山东海化地区历史实际 8760 小时的风光资源和负荷数据。这可能包括风电和光伏的发电曲线，园区的厂用电基础负荷等。

2. 系统配置： 设计风光储氢系统，包含两类制氢设备、风电机组、光伏、电/氢两类储能设备等典型设备。确保系统满足全年制氢总产量目标为5000万标方，售氢价格为35元/kg。

3. 负荷约束： 以签订售氢合同为例，制氢负荷需满足全年总产量目标，且单日产量不低于计划产量的 70%。这可能涉及制定相应的负荷约束条件。

4. 算例验证计算平台配置： 使用配置为 Intel(R) Core(TM) i5-8400 CPU，8.00G RAM 的计算平台。建模平台采用 Matlab2022a 仿真平台。

5. 建模： 根据提供的规划模型和求解方法，在Matlab中建立相应的数学模型。包括主问题和分解子问题，并调用 Gurobi 商用求解器进行求解。

6. 规划模型与求解方法验证： 针对现有制氢设备发展水平限制，验证所提出的规划模型与求解方法的可行性。考虑规划结果中包含10台及以上制氢设备，以及8760小时生产模拟下的变量与约束数量可能超过求解器求解能力的情况。

7. 对比分析： 设置三种方案进行对比分析。分别是：

   • 方案 1：?基于 8760 小时生产模拟的规划求解方法；
   • 方案 2：?根据风光资源分布，将全年分为夏季、冬季、过渡季三种典型日，在双层规划模型中基于典型日进行生产模拟；
   • 方案 3：?基于风光资源特点，采用 K-means 聚类生成 4 种典型场景，在双层规划模型中基于典型场景进行生产模拟。

8. 结果分析： 分析仿真结果，比较三种方案的优劣。考察是否方案1能够更准确地满足制氢负荷约束，以及是否在实际情况下比其他两种方案更为可行。

由于具体的算法和模型细节未提供，下面提供一个简化的伪代码示例，展示主要思路：

import gurobipy as gp
import numpy as np

# 数据准备
# 以下是示例数据，实际情况需要根据具体数据进行替换
wind_power_curve = np.array([/* 8760小时的风力发电曲线数据 */])
solar_power_curve = np.array([/* 8760小时的太阳能发电曲线数据 */])
base_load = 500  # 园区厂用电基础负荷

# 系统配置
hydrogen_target = 50000000  # 制氢总产量目标
hydrogen_price = 35  # 售氢价格
daily_production_constraint = 0.7  # 单日产量不低于计划产量的70%

# 算例验证计算平台配置
cpu_config = "Intel(R) Core(TM) i5-8400 CPU"
ram_config = "8.00G RAM"
simulation_platform = "Matlab2022a"
solver = "Gurobi"

# 建模
model = gp.Model("Hydrogen_Production_Planning")

# 添加变量
num_hours = len(wind_power_curve)
wind_power = model.addVars(num_hours, lb=0, ub=float('inf'), name="Wind_Power")
solar_power = model.addVars(num_hours, lb=0, ub=float('inf'), name="Solar_Power")
hydrogen_production = model.addVars(num_hours, lb=0, ub=float('inf'), name="Hydrogen_Production")

# 添加约束
model.addConstrs((wind_power[i] + solar_power[i] >= base_load for i in range(num_hours)), name="Power_Balance")
model.addConstr(hydrogen_production.sum() == hydrogen_target, name="Hydrogen_Target")

# 添加目标函数
revenue = hydrogen_price * hydrogen_production.sum()
model.setObjective(revenue, sense=gp.GRB.MAXIMIZE)

# 调用求解器求解
model.optimize()

# 获取结果
if model.status == gp.GRB.OPTIMAL:
    # 输出优化结果
    print("Optimal Solution Found:")
    print(f"Total Revenue: {model.objVal}")

    # 输出风光发电和制氢量等信息
    for i in range(num_hours):
        print(f"Hour {i + 1}: Wind Power = {wind_power[i].x}, Solar Power = {solar_power[i].x}, Hydrogen Production = {hydrogen_production[i].x}")

    # 其他结果处理
    # ...
else:
    print("Optimization Problem is infeasible or unbounded.")

# 对比分析
# ...

# 输出结果
# ...

请注意，上述代码仅为示例，实际情况下需要根据具体问题进行适当修改和调整。这包括添加更多的约束、调整目标函数，以及根据具体问题的需求进行结果的详细分析。此外，该示例中使用了Gurobi作为求解器，确保您已安装Gurobi并具有相应的许可证。