代码随想录刷题题Day35

刷题的第三十五天，希望自己能够不断坚持下去，迎来蜕变。😀😀😀
刷题语言：C++
Day35 任务
● 121. 买卖股票的最佳时机
● 122.买卖股票的最佳时机II

1 买卖股票的最佳时机

121. 买卖股票的最佳时机

思路：
暴力
找最优间距
C++：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        for (int i = 0; i < prices.size(); i++) {
            for (int j = i + 1; j < prices.size(); j++) {
                result = max(result, prices[j] - prices[i]);
            }
        }
        return result;
    }
};

时间复杂度：$O(n^2)$
空间复杂度：$O(1)$
该方法超时

---

贪心
因为股票就买卖一次，那么贪心的想法很自然就是取最左最小值，取最右最大值，那么得到的差值就是最大利润
C++：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int low = INT_MAX;
        int result = 0;
        for (int i = 0; i < prices.size(); i++) {
            low = min(low, prices[i]);// 取最左最小价格
            result = max(result, prices[i] - low);// 直接取最大区间利润
        }
        return result;
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(1)$

---

动态规划
（1）确定dp数组（dp table）以及下标的含义

dp[i][0] 表示第i天持有股票所得最多现金
dp[i][1] 表示第i天不持有股票所得最多现金

（2）确定递推公式

如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来

1.第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
2.第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]
dp[i][0]应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i]);

第i天不持有股票即dp[i][1]

1.第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
2.第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]

$dp[i][1]=max(dp[i?1][1],prices[i]+dp[i?1][0]);$
（3）dp数组如何初始化
dp[0][0] -= prices[0]
dp[0][1] = 0
（4）遍历顺序：从前向后遍历
（5）举例推导dp数组

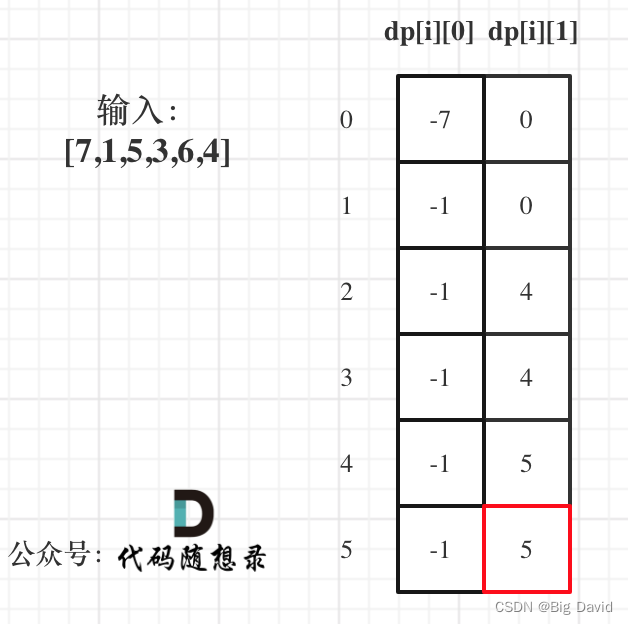
本题中不持有股票状态所得金钱一定比持有股票状态得到的多
C++：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if (len == 0) return 0;
        vector<vector<int>> dp(len, vector<int>(2));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], -prices[i]);
            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
        }
        return dp[len - 1][1];
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(n)$

2 买卖股票的最佳时机II

122.买卖股票的最佳时机II

思路：
动态规划
dp[i][0] 表示第i天持有股票所得现金。
dp[i][1] 表示第i天不持有股票所得最多现金

如果第i天持有股票即dp[i][0]， 那么可以由两个状态推出来:
1.第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金 即：dp[i - 1][0]
2.第i天买入股票，所得现金就是昨天不持有股票的所得现金减去 今天的股票价格 即：dp[i - 1][1] - prices[i]

如果第i天不持有股票即dp[i][1]的情况， 依然可以由两个状态推出来
1.第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金 即：dp[i - 1][1]
2.第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]

C++：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len, vector<int>(2, 0));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[len - 1][1];
    }
};

时间复杂度：$O(n)$
空间复杂度：$O(n)$

---

鼓励坚持三十六天的自己😀😀😀