C++基础算法之贪心
临渊羡鱼
不如退而结网
🔥个人专栏
寒假带大家手撕算法
期待小伙伴们的支持与关注！！！
目录
贪心算法的简介?
贪心算法的介绍#
贪心算法(greedy algorithm) ：是用计算机来模拟一个[贪心]的人做出决策的过程。个人十分贪婪，每一步行动总是按某种指标选取最优的操作。而且他目光短浅，总是只看眼前并不考虑以后可能造成的影响。可想而知，并不是所有的时候贪心法都能获得最优解，所以一般使用贪心法的时候，都要确保自己能证明其正确性。
(贪心算法可以比喻为：贪婪+鼠目寸光)
例如#
小明现在有100元钱，他希望购买尽可能多的商品，请问最多能买多少商品。如果这个问题用贪心的思维想，便是我们每次都尽可能买价格最低的商品，我们最后购买的商品数量一定是最多的，这便是贪心算法。
贪心的基本原理#
<1>根据当前情况，做出一步最佳选择
<2>做出选择后，永不改变，永不反悔
<3>如此循环，用局部最优解，逐步得到整体最优解
贪心的局限性#贪心算法不能保证获得全局最优解，但在某些问题上具有高效性
贪心的特征#贪心选择性质、最优子结构性质
<1>贪心策略的提出
#贪心策略的提出是没有标准以及模板的
#可能每一道题的贪心策略都是不同的
<2>贪心策略的正确性
#因为有可能 贪心策略 是一个错误的方法
#正确的贪心策略，我们是需要证明的
贪心算法的解题步骤#
<1>建立数学模型来描述问题
<2>把求解的问题分成若干个子问题
<3>对每一子问题求解，得到子问题的局部最优解
<4>把子问题的解局部最优解合成原来解问题的一个解
贪心算法的运用与模型
最小化战斗力差距
题目链接：最小化战斗力差距
题目描述#
小蓝是机甲战队的队长，他手下共有n名队员，每名队员都有一个战斗力值wi。现在他需要将这n名队友分成两组a和b，分组必须满足以下条件：
<1>每个队友都属于a组或6组。
<2>a组和6组都不为空。
<3>战斗力差距最小。
战斗力差距的计算公式为 |max(a)- min(b)| ，其中max(a)表示a组中战斗力最大的，min(b)表示b组中战斗力最小的。
请你计算出可以得到的最小战斗力差距。输入格式#
第一行一个整数n，表示队员个数。
第二行n个整数w1,w2,w3....wn，分别表示每名队友的战斗力值数据范围保证：2<=n<=10^5，1<=wi<=10^9。
输出格式#
输出一个整数，表示可以得到的最小战斗力差距。
样例输入#
3 1 2 3样例输出#
1
思路#
排序模型
但是如果把所有解一一枚举，那工程量就很大，效率不高
我们可以借助排序的办法
要将战斗力分为两部分，为了使得差距最我们可以将战斗力排序后，找一个位置进行划分，使得左边的都在a，右边的都在b，从而这个差距就是这个位置两边的战斗力差距，说明差距的取值仅有n-1种，枚举即可。
本题排序之后是不会影响最终结果的而且更高效
在贪心算法中我们经常要用到排序
#include<bits/stdc++.h> using namespace std; int main() { int n; cin>>n; vector<int> str(n); //开辟动态空间 for(int i = 0;i<n;i++) { cin>>str[i]; } sort(str.begin(),str.end()); //快速排序 int k = str[1] - str[0]; for(int i = 1;i<n;i++) { k = min(k,str[i]-str[i-1]);//求最小的战力差 } cout<<k<<endl; return 0; }
纪念品分组
题目链接：纪念品分组
题目描述#
元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品，并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组的数目最少。
你的任务是写一个程序，找出所有分组方案中分组数最少的一种，输出最少的分组数目。输入描述#
第1行包括一个整数w(8<=w<=200)，为每组纪念品价格之和的上限。
第2行为一个整数n(1<=n<=30000)，表示购来的纪念品的总件数。
第3~n+2行每行包含一个正整数pi(5<=pi<=w)，表示所对应纪念品的价格。?
输出描述#
输出一行，包含一个整数，即最少的分组数目。
输入输出样例#
输入#
100 9 90 20 20 30 50 60 70 80 90输出#
6
思路#
最少数目模型
为了使得组数最小，我们应该使得每一组内尽可能装两件礼物 (最多只能装两件)尽量占满一组的容量所以贪心策略是，每一个贵的礼物带一个便宜的，因为带也是一组，不带也是一组，肯定选择带，且最贵的和最便宜的最容易占满一组。
#include<bits/stdc++.h> using namespace std; int main() { int w,n; cin>>w>>n; vector<int> p(n); for(int i = 1;i<=n;i++) { cin>>p[i]; } sort(p.begin(),p.end()); int left = 1,right = n,count = 0; while(left<=right) { if(left == right) { count++; break; } if((p[left]+p[right])<=w) { count++; left++; right--; } else { right--; count++; } } cout<<count<<"\n"; return 0; }
谈判
题目链接：谈判
题目描述#
在很久很久以前，有n个部落居住在平原上，依次编号为1到n。第 i 个部落的人数为ti。
有一年发生了灾荒。年轻的政治家小蓝想要说服所有部落一同应对灾荒，他能通过谈判来说服部落进行联合。每次谈判，小蓝只能邀请两个部落参加，花费的金币数量为两个部落的人数之和，谈判的效果是两个部落联合成一个部落(人数为原来两个部落的人数之和)。
输入描述#输入的第一行包含一个整数n，表示部落的数量第二行包含n个正整数，依次表示每个部落的人数其中,1<=n<=1000，1 <=ti<= 10^4。
输出描述#输出一个整数，表示最小花费。
输入输出样例#输入#
4 9 1 3 5输出#
31
思路#
最小代价模型
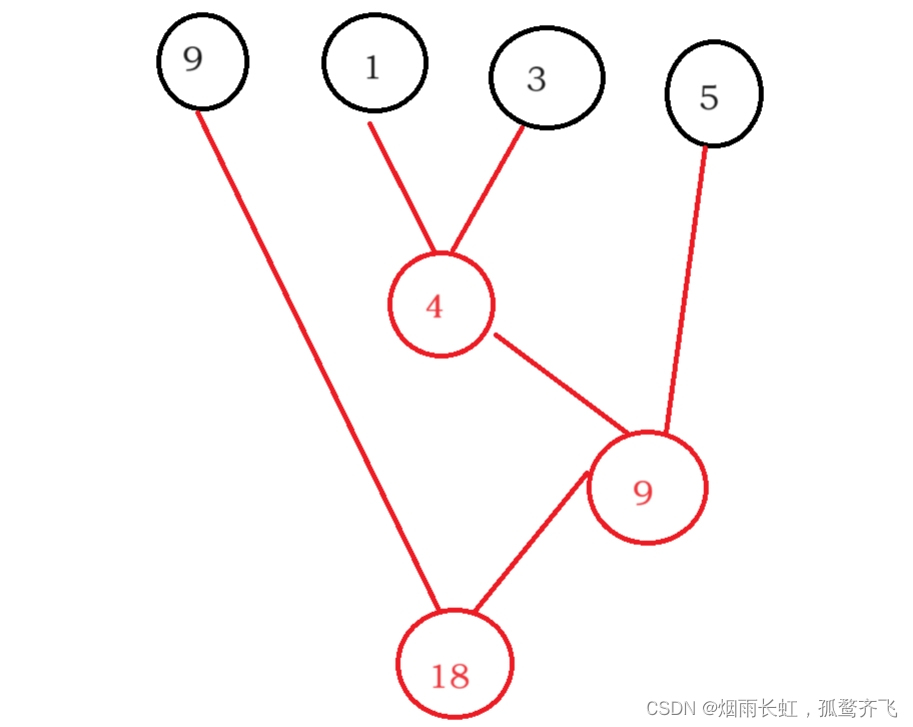
我们知道这里一共需要进行的操作次数一定是n-1次，那么贪心地想，如果每次选择代价最小的两个部落合并不仅可以使得当前代价最小，还可以使得后续合并的代价也尽可能小部落大小通过优先队列来维护。
31 = 4 +9+18
#include<bits/stdc++.h> using namespace std; using ll = long long; priority_queue<ll,vector<ll>,greater<ll>> pq;//优先队列 int main() { int n; cin>>n; for(int i = 1;i<=n;i++) { ll x; cin>>x; pq.push(x); //将元素x插入优先队列里 } ll ans = 0; while(pq.size()>1) { ll x = pq.top();//返回优先队列顶部元素 pq.pop(); //弹出优先队列顶部元素 ll y = pq.top(); pq.pop(); ans += x+y; //计算人数相对较小的两个部落之和 pq.push(x+y); } cout<<ans<<"\n"; return 0; }
补充#?
priority_queue按照元素的值从大到小进行排序，即最大元素位于队列的前面
可以直接使用greater<T>来修改比较方法，使最小元素位于队列的前面
push（x）? -将元素 x 插入到优先队列中
pop（）? ??-弹出优先队列中的顶部元素
top（）? ? ?-返回优先队列中的顶部元素
empty（）-检查优先队列是否为空
size（）? ? -返回优先队列中元素的个数
将数组和减半的最小操作数
题目链接：将数组和减半的最小操作数
给你一个正整数数组?
nums?。每一次操作中，你可以从?nums?中选择?任意?一个数并将它减小到?恰好?一半。（注意，在后续操作中你可以对减半过的数继续执行操作）请你返回将?
nums?数组和?至少?减少一半的?最少?操作数。示例 1：
输入：nums = [5,19,8,1] 输出：3 解释：初始 nums 的和为 5 + 19 + 8 + 1 = 33 。 以下是将数组和减少至少一半的一种方法： 选择数字 19 并减小为 9.5 。 选择数字 9.5 并减小为 4.75 。 选择数字 8 并减小为 4 。 最终数组为 [5, 4.75, 4, 1] ，和为 5 + 4.75 + 4 + 1 = 14.75 。 nums 的和减小了 33 - 14.75 = 18.25 ，减小的部分超过了初始数组和的一半，18.25 >= 33/2 = 16.5 。 我们需要 3 个操作实现题目要求，所以返回 3 。 可以证明，无法通过少于 3 个操作使数组和减少至少一半。示例 2：
输入：nums = [3,8,20] 输出：3 解释：初始 nums 的和为 3 + 8 + 20 = 31 。 以下是将数组和减少至少一半的一种方法： 选择数字 20 并减小为 10 。 选择数字 10 并减小为 5 。 选择数字 3 并减小为 1.5 。 最终数组为 [1.5, 8, 5] ，和为 1.5 + 8 + 5 = 14.5 。 nums 的和减小了 31 - 14.5 = 16.5 ，减小的部分超过了初始数组和的一半， 16.5 >= 31/2 = 15.5 。 我们需要 3 个操作实现题目要求，所以返回 3 。 可以证明，无法通过少于 3 个操作使数组和减少至少一半。提示：
1 <= nums.length <= 10^51 <= nums[i] <= 10^7
思路#
最小代价模型
<1>每次挑选当前数组中，最大的那个数，然后减半
<2>直到数组和减少到至少一半为止
class Solution { public: int halveArray(vector<int>& nums) { priority_queue<double> pq;//优先队列 double sum = 0.0; int count = 0; for(auto x: nums)//遍历 { pq.push(x); //插入数据 sum += x; } sum/=2; while(sum>0) { double num = pq.top()/2.0;//提取顶部元素 pq.pop(); //弹出顶部元素 sum -= num; pq.push(num); //插入减半元素 count++; } return count; } };
柠檬水找零?
题目链接：柠檬水找零
在柠檬水摊上，每一杯柠檬水的售价为?
5?美元。顾客排队购买你的产品，（按账单?bills?支付的顺序）一次购买一杯。每位顾客只买一杯柠檬水，然后向你付?
5?美元、10?美元或?20?美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付?5?美元。注意，一开始你手头没有任何零钱。
给你一个整数数组?
bills?，其中?bills[i]?是第?i?位顾客付的账。如果你能给每位顾客正确找零，返回?true?，否则返回?false?。示例 1：
输入：bills = [5,5,5,10,20] 输出：true 解释： 前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。 第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。 第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。 由于所有客户都得到了正确的找零，所以我们输出 true。示例 2：
输入：bills = [5,5,10,10,20] 输出：false 解释： 前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。 对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。 对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。 由于不是每位顾客都得到了正确的找零，所以答案是 false。提示：
1 <= bills.length <= 10^5bills[i]?不是?5?就是?10?或是?20?
思路#
由图可知我们的贪心策略是：5块钱优先保留，避免以后出现只能找5块钱的情况
class Solution { public: bool lemonadeChange(vector<int>& bills) { int w = 0,s = 0;//w代表5块钱，s代表10块钱 for(auto x: bills) { if(x == 5)w++; else if(x == 10) { if(w == 0)return false; else { w--; s++; } } else if(x == 20) { if(w&&s) { w--; s--; } else if(w>=3)w-=3; else return false; } } return true; } };
分糖果?
题目链接：分糖果
问题描述#
最近暑期特训算法班的同学们表现出色，他们的老师肖恩决定给他们分发糖果。肖恩购买了n个不同种类的糖果，用小写的阿拉伯字母表示。每个糖果必须分发给一个同学，并且每个同学至少要分到一个糖果。同学们的开心程度定义为他们所分到的糖果组成的字符串s的字典序。肖恩希望同学们的开心程度相差尽量小，因此他要找到一种方案，使得所有糖果组成的字符串中字典序最大的字符串尽可能小。请输出能够实现字典序最小可能的
max(s[1],s[2],s[3],...,s[x])?。
输入描述#第一行输入两个整数 n 和 x，分别表示有n个糖果x个同学
第二行输入一个长度为n的字符串S，S[i]表示第个糖果的种类数据保证1<=n<=10^6，1<= x <=n,S[i]?∈ {'a'，'z'}；
输出描述#输出一个字符串，为所有糖果组成的字符串中字典序最大的字符串最小的可能值。
样例输入
6 2 caabdc样例输出
abccd
思路#
找规律的贪心类型
先给字符串排序，然后我们可以分为三类讨论：<1>字符串全相等(假设全a)，那就是尽量使得每个人分到的字符串的最大长度尽可能小就行
<2>S[x] == S[1]，说明第x个是最小的字符，它要带着后面所有的学符一起输出<3>S[x] != S[1]，后面一坨字符可以直接丢到S[1]后面，分给第一个同学
#include<bits/stdc++.h> #define N 1000000 using namespace std; int main() { int n,x; cin>>n>>x; char str[N]; cin>>str+1; sort(str+1,str+1+n); if(str[1] == str[n]) { for(int i = 1;i<= n/x+(n%x?1:0);i++)cout<<str[1]; } else if(str[1] == str[x]) { for(int i = x;i<=n;i++)cout<<str[i]; } else cout<<str[x]; return 0; }
总结#
贪心算法并不从整体最优考虑，它所作出的选择只是在某种意义上的局部最优选择。基本思路就是从问题的某一个初始解出发逐步逼近给定的目标，以尽可能快的地求得更好的解。贪心算法不局限于固定的模型，我们在做题的时候要学会总结规律。
?
?
?
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！