【史上最易懂】马尔科夫链-蒙特卡洛方法：基于马尔科夫链的采样方法，从概率分布中随机抽取样本，从而得到分布的近似

马尔科夫链-蒙特卡洛方法

• • 蒙特卡洛方法：从概率分布中随机抽取样本，从而得到分布的近似
  • • 采样
    • 第一个公式（s）的解读：理论上的期望值
    • 第二个公式（${\hat{s}}_n$）的解读：如何通过具体的数据样本来近似这个理论值
  • 马尔科夫链-蒙特卡洛方法

?

---

蒙特卡洛方法：从概率分布中随机抽取样本，从而得到分布的近似

蒙特卡洛方法：一种近似复杂概率分布的随机采样方法。

假设你有一家包子店，但你不确定每天应该准备多少个包子。

你知道如果包子不够卖，会失去收入；如果包子剩太多，又会浪费食材。

问题是，你不知道每天会来多少顾客，每个顾客会买多少个包子。

• 多备货带来的浪费成本
• 少备货带来的顾客流失成本

这时候，你可以用一种叫做蒙特卡洛方法的技巧来帮助你做决策。

这个方法的基本思想是这样的：

1. 观察：首先，你观察过去几天或几周的情况，记录下来工作日和周末每天的顾客数量，以及他们买的包子数量。

2. 模拟：接着，你通过这些信息来模拟可能的情况。比如，你可以用抽签的方式来决定明天每个顾客可能的行为。每个签上写着“买1个包子”或“买2个包子”这样的信息。

3. 重复：你把这个过程重复100次。就像你有100个不同的明天，每个明天都可能有不同的顾客数和购买情况。

4. 计算：每次模拟结束后，你计算一下如果是这种情况，你的店会有多少利润。比如，如果张三来了买1个包子，李四买了2个，总共卖出的包子数量和利润是多少。

5. 平均：最后，你把这100次模拟的利润加起来，然后除以100，得到一个平均值。这个平均值可以告诉你，基于以往的情况，你可以期望的大概利润是多少。

蒙特卡洛方法就像是你在做一个实验，通过反复随机模拟明天的情况，来帮助你决定应该准备多少个包子。

• 是一种模拟算法，每个样本都代表着一次对现实的模拟。我们用有限次的模拟，来替代了所有的可能性。

换成数学语言就是 – 蒙特卡洛方法就是对问题中的随机事件进行取样，为有限个样本进行独立计算，最后把样本结果进行统计的策略。

什么时候可以采用蒙特卡洛法？

• 可能性太多，我们计算不了的时候用的。

蒙特卡洛的性质：

• 是对问题的估算，而不是精确计算。
• 非常依赖参数和模型的正确。

?

---

采样

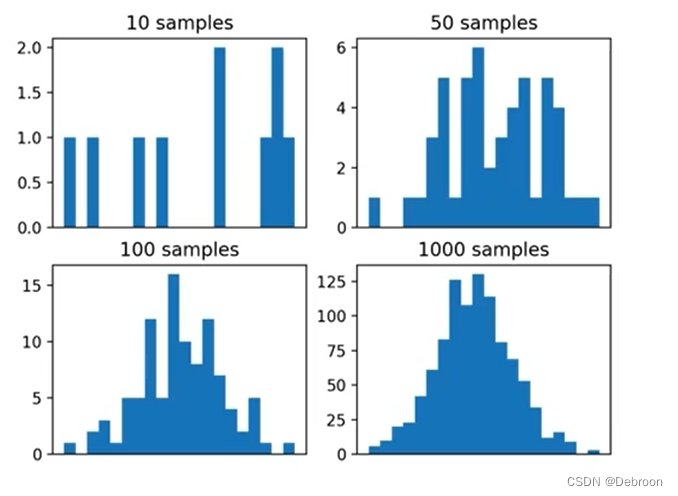
蒙特卡洛的采样，是从概率分布中随机抽取样本，从而得到分布的近似。

• 样本越多，采样越准确

$\begin{array}{rl}s& =\int p(\mathbf{x})f(\mathbf{x})d\mathbf{x}=E_p[f(\mathbf{x})]\\ & \\ {\hat{s}}_n& =\frac{1}{n}\sum _{i=1}^{n}f({\mathbf{x}}^{(i)}).\end{array}$

• 如何通过随机变量的分布来计算某个函数的期望值
• 如何利用样本来估计这个期望值

第一个公式（s）的解读：理论上的期望值

• s 是一个数学期望（平均值），我们可以想象一个随机过程，比如抽签，每次抽签都对应一个结果 x，并且每个结果 x 都有一个概率 p(x)。

• 函数 f(x) 是我们对每次抽出的结果 x 做的某种操作，比如可以是计算 x 的平方、加倍等等。

• 公式中的 ∫ p(x)f(x)dx 是一个积分，意思是对所有可能的结果 x，将每个结果的概率 p(x) 与操作后的值 f(x) 相乘，然后把这些乘积加在一起。这就给了我们一个加权平均，也就是 s。

• 这个期望值 s 是说：如果我们无限次地重复抽签过程，每次都对结果做操作 f(x)，那么平均下来，每次操作的结果会是多少。

第二个公式（${\hat{s}}_n$）的解读：如何通过具体的数据样本来近似这个理论值

• ${\hat{s}}_n$ 是对上述期望值 s 的一个估计。因为在实际中，我们无法无限次重复实验，所以我们只能通过有限次数的抽样来估计期望值。
• $\frac{1}{n}{\sum }_{i=1}^{n}f({\mathbf{x}}^{(i)})$ 是一个平均值，是说：我们实际上只进行了 n 次抽签，并且记录下了每次抽签的结果 x。对于每次抽签，我们都计算 f(x)，然后把这 n 个 f(x) 加起来，除以 n，得到一个平均值。
• 这个平均值 ${\hat{s}}_n$ 就是我们对实际期望值 s 的一个估计。
• 我们希望随着 n（样本数量）的增加，我们的估计 ${\hat{s}}_n$ 越来越接近真实的期望值 s。

这个公式的问题在于，实践中，某个概率分布 $p(x)f(x)$ 难以采样。

数学上提供了 重要性抽样（Importance sampling），解决这个问题。

• 重要性抽样解决了，在计算随机变量的期望值或复杂概率分布时，遇到的计算困难或无法直接计算的问题。
• 使用一个已知（易于采样）的概率分布来生成样本，并根据该样本的重要性权重对期望值进行重新加权。

以下就是重要性抽样的数学公式：

$\begin{array}{rl}p(\mathbf{x})f(\mathbf{x})& =q(\mathbf{x})\frac{p(\mathbf{x})f(\mathbf{x})}{q(\mathbf{x})}.\\ {\hat{s}}_q& =\frac{1}{n}\sum _{i=1,{\mathbf{x}}^{(i)}～q}^n\frac{p({\mathbf{x}}^{(i)})f({\mathbf{x}}^{(i)})}{q({\mathbf{x}}^{(i)})}\end{array}$

• $q(\mathbf{x})$：一个已知（易于采样）的概率分布
• 从概率分布中抽取 n 个样本，$i$ 表示样本的索引

马尔科夫链-蒙特卡洛方法

当问题涉及到高维空间，使用重要性抽样 + 蒙特卡洛方法，还是难以计算。

• 需要采样大量样本，才能保证精度

我们可以使用马尔科夫链的蒙特卡洛方法来解决这个问题。

• 用马尔科夫链进行采样，可以从任意分布、任意状态采样
• 是一种迭代策略，首先定义随机变量转移矩阵（可以将当前状态转移到下一个状态）
• 因为这些状态是转移矩阵随机生成，最终状态序列会收敛到一个目标分布

比如在巨大城堡，里面有很多房间，找到每个房间里的人数分布情况（每个房间被访问的次数），但是你不能一次进入所有的房间并计数。

你从房间A开始，记录房间A里的人数。

然后，根据一个规则（假设转移概率是基于房间的人数，人数较多的房间具有较高的转移概率），你随机选择一个相邻的房间作为下一个状态。

你进入该房间，记录房间的人数，并再次根据规则选择下一个房间。

你不断重复这个过程，记录不同房间的人数。

因为你是根据随机规则进行选择的，所以你会以一种随机的方式在不同的房间之间移动。

但是，当你重复这个过程很多次时，你会发现你更有可能停留在人数更多的房间，而在人数较少的房间停留的次数较少。

• 通过计算每个房间被访问的频率，来估计每个房间的人数分布情况。

你最终会得到一个状态序列，其中房间的停留次数与该房间的人数成正比。

当你重复这个过程很多次时，你会更多地停留在人数较多的房间，从而获得与人数分布相关的结果。

虽然你不能直接计算每个房间的人数，但通过马尔科夫链的蒙特卡洛方法，你可以从任意状态（房间）开始采样，并最终收敛到目标分布（人数分布）。