D49|动态规划之回文子串

首先复习一下，回文串是正读和反读都是一样的字符串。

647.回文子串

初始思路：

动态规划五部曲：

1）dp数组的定义

dp[i]表示到第i个位置，所拥有的回文子串的数目。

2）公式

我只想好了aa bb这种重复情况就比如，当前元素如果跟前一个不同dp[i] = dp[i-1]+1;如果相同的话dp[i] = dp[i-1]+x,对于这个x还没有一个固定的解析，同时没办法应对abba这种情况。

题解复盘：

动态规划五部曲：

1）dp数组的定义

那么此时我们是不是能找到一种递归关系，也就是判断一个子字符串（字符串的下表范围[i,j]）是否回文，依赖于，子字符串（下表范围[i + 1, j - 1]）） 是否是回文。

布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。

2）递推公式：

整体上是两种，就是s[i]与s[j]相等，s[i]与s[j]不相等这两种。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

• 情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
• 情况二：下标i 与 j相差为1，例如aa，也是回文子串
• 情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

3）初始化：

dp[i][j]初始化为false。

4) 循环顺序：

所以一定要从下到上，从左到右遍历，这样保证dp[i + 1][j - 1]都是经过计算的。

注意j一定是大于等于i的

for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍历顺序
    for (int j = i; j < s.size(); j++) {
        if (s[i] == s[j]) {
            if (j - i <= 1) { // 情况一 和 情况二
                result++;
                dp[i][j] = true;
            } else if (dp[i + 1][j - 1]) { // 情况三
                result++;
                dp[i][j] = true;
            }
        }
    }
}

class Solution {
    public int countSubstrings(String s) {
        boolean[][] dp = new boolean[s.length()][s.length()];
        
        int res = 0;
        for (int i = s.length() - 1; i >= 0; i--) {
            for (int j = i; j < s.length(); j++) {
                if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
                    res++;
                    dp[i][j] = true;
                }
            }
        }
        return res;
    }
}

---

?516.最长的回文子序列

初始思路&&题解复盘：

1）dp数组的含义;

dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

2)

在判断回文子串的题目中，关键逻辑就是看s[i]与s[j]是否相同。

如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

如图：?

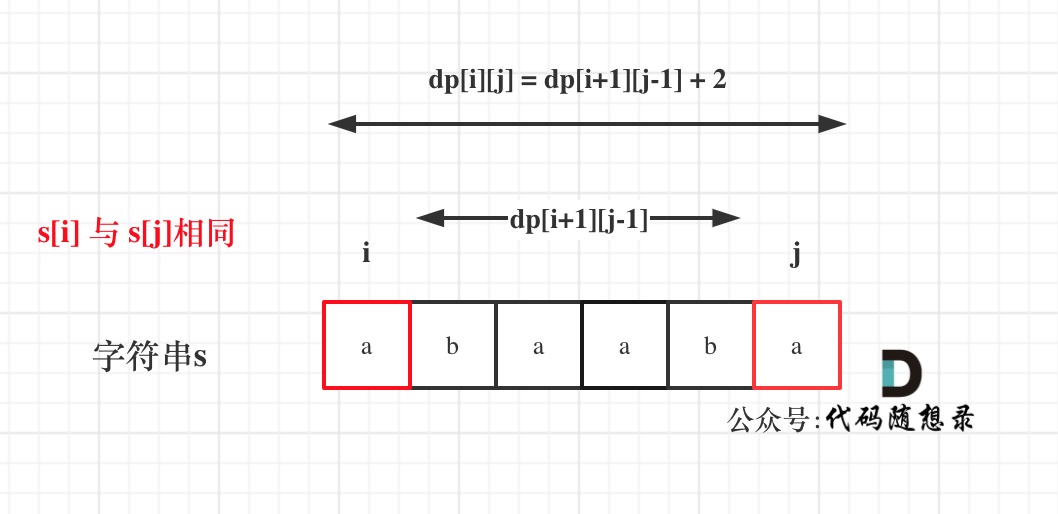
（如果这里看不懂，回忆一下dp[i][j]的定义）

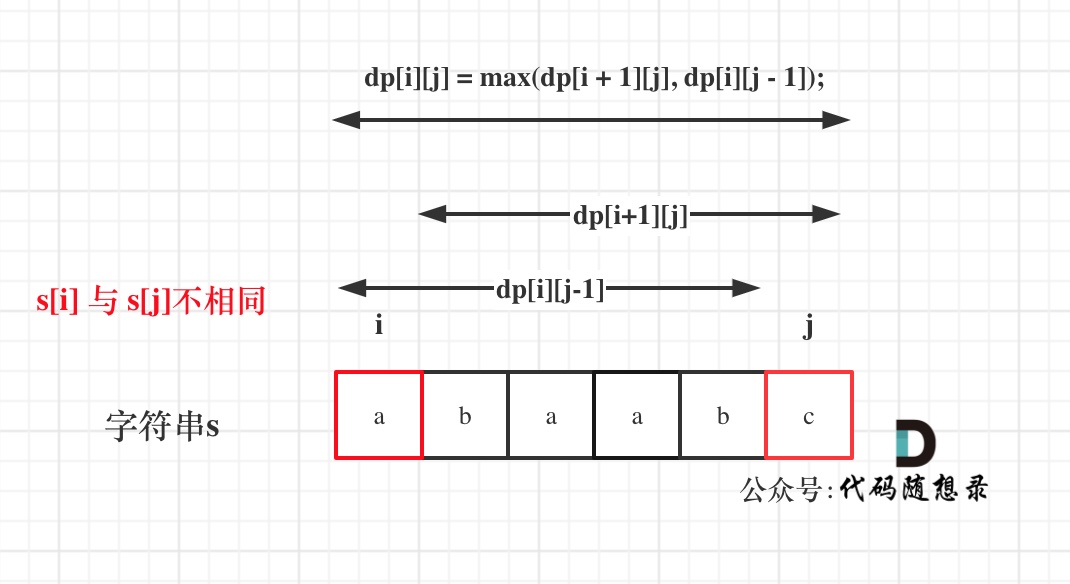
如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1][j]。

加入s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

这里一开始我有点迷糊，为什么要从baabc和abaab中取最大回文子序列的长度，咋能保证abaab中和baabc中一定是回文子序列呢，但是随后通过实例推导就可以发现，abaab中记录的长度其实还是baab的长度。

3）初始化：

对角线初始化为1；

4）遍历顺序：从下到上，从左到由，j大于i；

class Solution {
    public int longestPalindromeSubseq(String s) {
        int[][] dp = new int[s.length()][s.length()];
        int result = 1;
        for(int i = 0;i<s.length();i++){
            dp[i][i] = 1;
        
        }
        for(int i = s.length()-1;i>=0;i--){
            for(int j=i+1;j<s.length();j++){
                if(s.charAt(i)==s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1]+2;
                }else{
                    dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
                }
                result = Math.max(result,dp[i][j]);
            }
            
        }
        return result;
    }
}

?