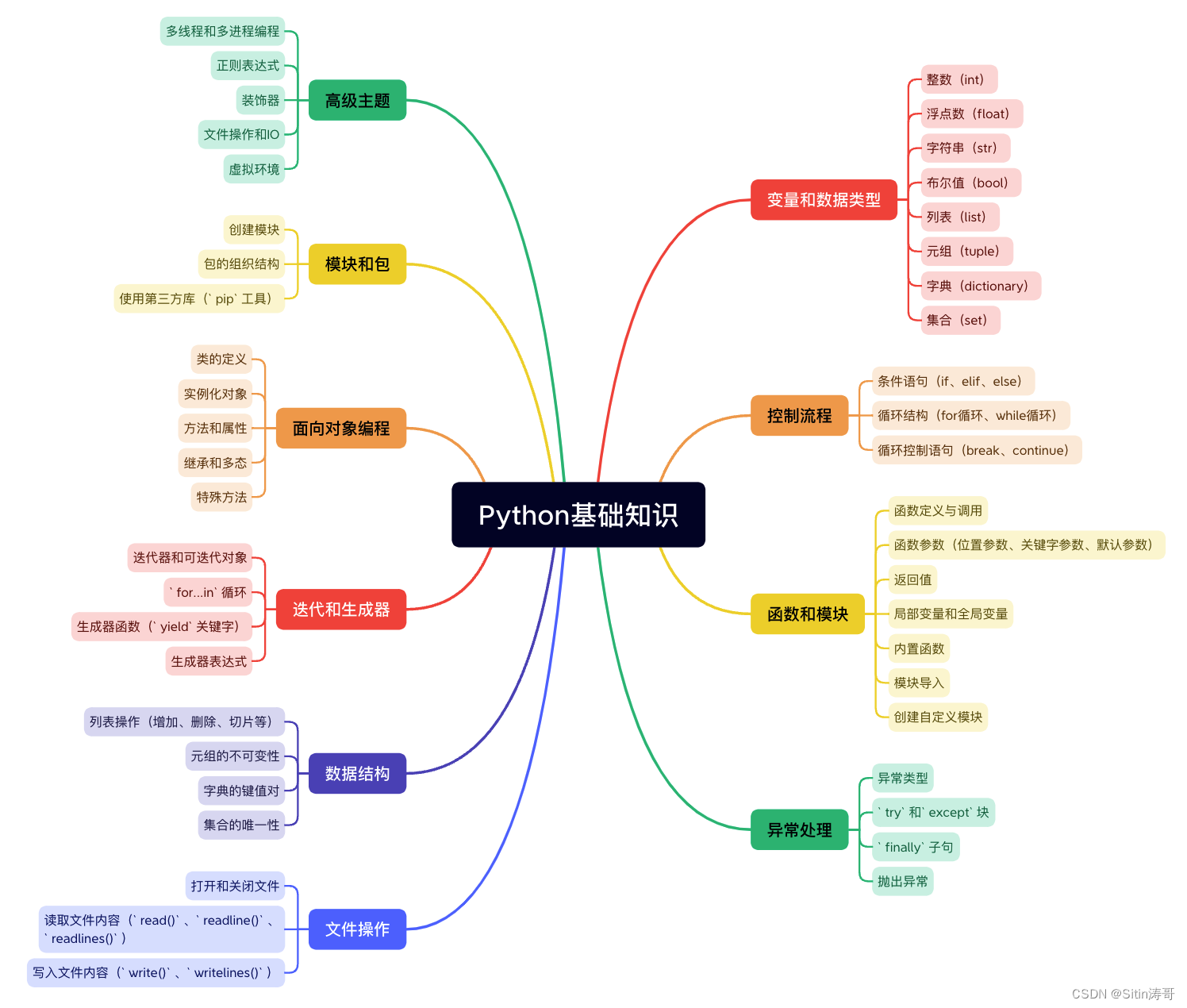
Python中杨辉三角形的生成、性质与应用

更多资料获取

📚 个人网站：ipengtao.com

---

杨辉三角形，又称帕斯卡三角形，是一个经典的数学图形，它具有许多有趣的性质和应用。杨辉三角形是一个由数字组成的三角形，每个数字等于它上方两个数字的和。本文将深入探讨杨辉三角形的生成方法、性质和一些实际应用，并提供详细的Python示例代码，帮助大家更好地理解和应用这个有趣的数学概念。

杨辉三角形的生成方法

1 基本概念

杨辉三角形的第一行只有一个数字1，接下来的每一行都以1开始和结束，并且中间的数字是上一行相邻两个数字的和。

例如，前几行杨辉三角形如下所示：

    1
   1 1
  1 2 1
 1 3 3 1
1 4 6 4 1

2 生成方法

杨辉三角形可以通过迭代的方式生成。从第一行开始，逐行计算下一行的数字，并将其添加到三角形中。

具体的生成方法如下：

1. 创建一个空列表triangle，用于存储杨辉三角形的每一行。
2. 初始化第一行为[1]，将其添加到triangle中。
3. 从第二行开始，每一行的第一个和最后一个数字都是1。
4. 对于中间的数字，计算它们等于上一行相邻两个数字的和。
5. 将每一行添加到triangle中，直到达到指定的行数。

下面是一个Python示例代码，演示如何生成前n行杨辉三角形：

def generate_pascals_triangle(n):
    triangle = []
    for i in range(n):
        row = [1]  # 第一个数字为1
        if triangle:
            last_row = triangle[-1]  # 获取上一行
            for j in range(1, i):
                # 计算中间数字
                row.append(last_row[j - 1] + last_row[j])
            row.append(1)  # 最后一个数字为1
        triangle.append(row)  # 将行添加到三角形中
    return triangle

# 生成前5行杨辉三角形
result = generate_pascals_triangle(5)
for row in result:
    print(row)

运行以上代码，将得到前5行杨辉三角形的输出。

杨辉三角形的性质

杨辉三角形有许多有趣的性质：

1 对称性

杨辉三角形是关于中心对称的，也就是说，如果将其沿着中心垂直线折叠，每个数字都与对称位置的数字相等。这个性质可以用来证明许多关于杨辉三角形的规律。

2 斜对角线

杨辉三角形中的斜对角线包含了一些有趣的数列，如斐波那契数列。例如，从第二行开始，每一条斜对角线都是斐波那契数列的一部分。这个性质可以用来计算斐波那契数列的和。

3 组合数

杨辉三角形中的每个数字表示一个组合数，即从n个元素中选择k个元素的方法数。例如，第3行的数字1、2、1分别表示从3个元素中选择0个、1个、2个元素的方法数。

4 幂展开

杨辉三角形中的每一行都对应着一个二项式展开式。例如，第4行的数字1、3、3、1对应着表达式(a + b)^3的展开系数。

杨辉三角形的应用

1 组合数学

杨辉三角形在组合数学中有广泛的应用。它可以用来计算组合数，解决排列组合问题，以及计算概率分布等。通过查找杨辉三角形中的特定数字，可以得到组合数的值，从而简化组合数学的计算。

2 概率分布

杨辉三角形可以用来生成二项分布的概率分布表。二项分布表示在多次独立重复的伯努利试验中成功的次数的概率分布。通过杨辉三角形，可以计算出不同试验次数和成功次数的概率。

3 数据压缩

杨辉三角形还可以用于数据压缩。通过将一行数字表示为前一行数字的差异，可以将数据压缩成更紧凑的形式。这种压缩方法称为差分编码。

杨辉三角形的应用示例

1 计算组合数

杨辉三角形可以用来计算组合数，即从n个元素中选择k个元素的方法数。

下面是一个Python示例代码，演示如何使用杨辉三角形计算组合数：

def compute_combinations(n, k):
    triangle = generate_pascals_triangle(n + 1)  # 生成n+1行的杨辉三角形
    return triangle[n][k]

  # 返回组合数

# 计算从10个元素中选择3个元素的组合数
result = compute_combinations(10, 3)
print(result)  # 输出 120

2 生成二项分布概率分布表

杨辉三角形可以用来生成二项分布的概率分布表。

下面是一个Python示例代码，演示如何生成二项分布的概率分布表：

def generate_binomial_distribution(n, p):
    distribution = []
    for k in range(n + 1):
        probability = compute_combinations(n, k) * (p ** k) * ((1 - p) ** (n - k))
        distribution.append(probability)
    return distribution

# 生成n=10, p=0.5的二项分布概率分布表
result = generate_binomial_distribution(10, 0.5)
for k, probability in enumerate(result):
    print(f"P(X = {k}) = {probability:.4f}")

总结

杨辉三角形是一个有趣且有用的数学概念，它不仅可以用来生成美丽的图形，还可以应用于组合数学、概率分布和数据压缩等领域。通过本文介绍的生成方法、性质和应用示例，可以更好地理解和应用杨辉三角形，从而在数学和编程中受益匪浅。希望本文对大家有所帮助，激发对数学和编程的兴趣，进一步探索这个有趣的数学领域。

---

Python学习路线

更多资料获取

📚 个人网站：ipengtao.com

如果还想要领取更多更丰富的资料，可以点击文章下方名片，回复【优质资料】，即可获取 全方位学习资料包。

点击文章下方链接卡片，回复【优质资料】，可直接领取资料大礼包。