随机微分方程数值实验 Euler-Maruyama方法（matlab）

发布时间：2023年12月26日

求解随机微分方程如下：

$\left\{\begin{array}{l}d X=1.6 X d t+2.3 X d W \\ X(0)=X_0=1\end{array}\right.$

微分方程的真解为：

$X(t)=X(0) e^{\left(1.6-\frac{1}{2} * 2.3^2\right) t+2.3 W(t)}$

Euler-Maruyama方法的数值格式：

$X_j=X_{j-1}+\left(1.6 X_{j-1}\right) \Delta t+2.3 X_{j-1}\left(W\left(\tau_j\right)-W\left(\tau_{j-1}\right)\right)$

程序如下：

randn('state',50)
lambda=1.6;mu=2.3;Xzero=1;
T=1;N=2^8;dt=1/N;
 dW=sqrt(dt)*randn(1,N);
 W=cumsum(dW);
 Xtrue=Xzero*exp((lambda-0.5*mu^2)*(dt:dt:T)+mu*W);
 plot([0:dt:T],[Xzero,Xtrue],'g-'),hold on 
 R=1;Dt=R*dt;L=N/R;
 Xem=zeros(1,L);
 Xtemp=Xzero;
 for j=1:L
     Winc=sum(dW(R*(j-1)+1:R*j));
     Xtemp=Xtemp+Dt*lambda*Xtemp+mu*Xtemp*Winc;
     Xem(j)=Xtemp;
 end
 plot([0:Dt:T],[Xzero,Xem],'r--*'),hold off
 xlabel('t','FontSize',20)
 ylabel('X','FontSize',20,'Rotation',0,'HorizontalAlignment','right')
 title('R=1时数值模拟示意图')
 emerr=abs(Xem(end)-Xtrue(end))
% Mean-square and asymptotic stability test for E-M

randn('state',150)
T=15;M=40000;Xzero=1;
ltype={'g-','r--','b-.'};
subplot(211)
lambda=1.6;mu=2.3;
for k=1:3
    Dt=2^(1-k);
    N=T/Dt;
    Xms=zeros(1,N);Xtemp=Xzero*ones(M,1);
    for j=1:N
        Winc=sqrt(Dt)*randn(M,1);
        Xtemp=Xtemp+Dt*lambda*Xtemp+mu*Xtemp.*Winc;
        Xms(j)=mean(Xtemp.^2);
    end
    semilogy([0:Dt:T],[Xzero,Xms],ltype{k},'Linewidth',2),hold on
end
legend('\Delta t=1','\Delta t=1/2','\Delta t=1/4')
title('Mean-Square:\lambda=1.6,\mu=2.3','FontSize',16)
ylabel('E[x^2]','FontSize',12),axis([0,T,1e-20,1e+20]),hold off
randn('state',130)
lambda=1.6;mu=2.3;Xzero=1;
T=1;N=2^8;dt=1/N;
 dW=sqrt(dt)*randn(1,N);
 W=cumsum(dW);
 Xtrue=Xzero*exp((lambda-0.5*mu^2)*(dt:dt:T)+mu*W);
 plot([0:dt:T],[Xzero,Xtrue],'g-'),hold on 
 R=4;Dt=R*dt;L=N/R;
 Xem=zeros(1,L);
 Xtemp=Xzero;
 for j=1:L
     Winc=sum(dW(R*(j-1)+1:R*j));
     Xtemp=Xtemp+Dt*lambda*Xtemp+mu*Xtemp*Winc;
     Xem(j)=Xtemp;
 end
 plot([0:Dt:T],[Xzero,Xem],'r--*'),hold off
 xlabel('t','FontSize',16)
 ylabel('X','FontSize',16,'Rotation',0,'HorizontalAlignment','right')
 title('R=4,randn(state,130)时数值模拟示意图')
 emerr=abs(Xem(end)-Xtrue(end))

结果：

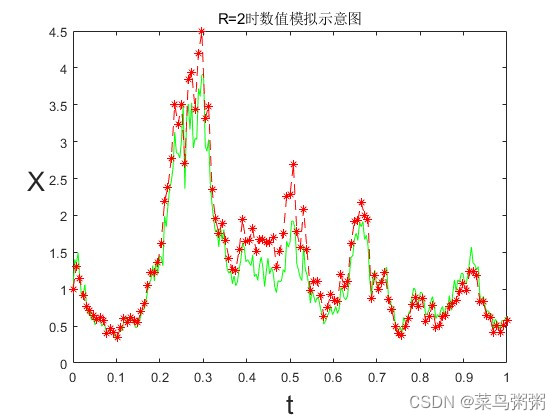
文章来源:https://blog.csdn.net/2301_76767110/article/details/135186871
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章