NLP论文阅读记录-ACL 2023 | 10 Best-k Search Algorithm for Neural Text Generation

---

前言

用于神经文本生成的 Best-k 搜索算法（2211）

code
paper

---

0、论文摘要

现代自然语言生成范式需要良好的解码策略才能从模型中获得高质量的序列。
集束搜索产生高质量但低多样性的输出；
随机方法存在高方差和有时低质量的问题，但输出往往更加自然和富有创意。
在这项工作中，我们提出了一种平衡质量和多样性的确定性搜索算法。
我们首先研究普通的最佳优先搜索 (BFS) 算法，然后提出 Best-k 搜索算法。
受 BFS 的启发，我们贪婪地扩展前 k 个节点，而不是仅扩展第一个节点，以提高效率和多样性。
增加最近发现的节点的权重并进行堆修剪可确保搜索过程的完整性。
对四个 NLG 任务（包括问题生成、常识生成、文本摘要和翻译）的实验表明，与强基线相比，best-k 搜索产生更加多样化和自然的输出，同时我们的方法保持了较高的文本质量。
所提出的算法无参数、轻量级、高效且易于使用1。

一、Introduction

1.1目标问题

大规模预训练语言模型最近取得的成功（Devlin 等人（2019）；Raffel 等人（2020）；Brown 等人（2020）；Nijkamp 等人（2022）等）显着在文本摘要、机器翻译、对话生成等任务上推进了自然语言生成领域的发展。尽管模型在流畅性、表达力和领域泛化方面的能力不断增强，但这些模型生成的输出还远远不够完美（Gehman 等人，2017）。 ，2020 年；Kryscinski 等人，2020 年；Fabbri 等人，2021 年）。如今，随着 LM 变得越来越大、越来越好，解码策略是这一代的另一个关键部分
通过从模型中提取高概率输出序列来释放 LM 的力量的范例。如果我们将文本生成视为一个搜索问题，那么解码策略本质上就是在词汇 V 组成的空间上的搜索算法。束搜索（Beam search）是一种基于剪枝的启发式搜索算法，多年来一直是首选。然而，生成的序列通常是重复的，因为许多多样化且有价值的假设在搜索的早期阶段被修剪（Eikema 和 Aziz，2020）。基于采样的方法（Fan et al., 2018；Holtzman et al., 2020）确实可以生成更加多样化的序列，但由于其随机性，它们很难控制。有时输出是重复的；有时，具有高方差的采样选择会破坏整个序列。它也没有提供比当前步骤更早扩展节点的灵活性，类似于波束搜索中的剪枝效果。

1.2相关的尝试

1.3本文贡献

我们正在寻找一种具有高度灵活性和可控性的解码算法，同时它还可以为某些用例产生不同的输出。我们发现最佳优先搜索（BFS）算法是理想的，满足这些性质。首先，作为一种确定性算法，它不会引入额外的方差。更重要的是，由于它不会修剪假设，因此它保留了更多样化的选项集，并允许同时扩展不同长度的假设。尽管有这些有趣的功能，但经过初步研究，我们发现将其应用于文本生成存在一些挑战。搜索效率和搜索完整性是阻碍BFS应用的两个主要因素。
因此，在这项工作中，我们提出了用于多样化和高质量文本生成的Bestk搜索算法。我们的方法通过一些设计更改重新发明了 BFS，以克服前面提到的问题。并行探索旨在每次探索搜索前沿中的前 k 个节点，而不是 BFS 中的一个。它将 BFS 速度提高了约 10 倍，在效率方面可与波束搜索相媲美。我们还在算法中添加了时间衰减机制以鼓励搜索完成。设计了一种简单而有效的无状态评分函数，作为更复杂的长度调整对应函数的替代方案，我们证明它运行良好，并有助于进一步查找不同的文本。
为了验证所提出的算法，我们对问题生成、常识生成、文本摘要和机器翻译四个任务进行了综合实验。我们的结果表明，所提出的算法适用于六个数据集上的各种模型。我们的方法在保持质量的同时产生高保真、多样化和自然的输出。

总之，我们的贡献如下：
（1）研究文本生成的最佳优先搜索；
(2)提出一种高效、简单、确定性的解码算法bestk-k搜索； （
3）通过消融研究和分析在六个数据集上进行了全面的实验和强有力的结果；
(4)算法免训练、免参数、轻量级、易用、兼容任何LLM。它也与许多解码技术（例如采样或推出）正交。

二.相关工作

重新审视最佳优先搜索
在本节中，我们将在自然语言生成的背景下介绍普通的 bestfirst 搜索作为解码算法，并讨论第一个研究问题：BFS 是在文本生成中搜索假设的好算法吗？

设置 文本生成可以表示为给定输入 x 和由 θ 参数化的概率语言模型2 的序列生成过程。
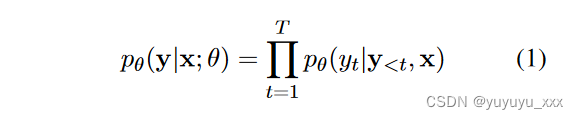传统上，采用最大后验 (MAP) 解码策略来引出最高得分的输出序列 arg maxy* pθ(y*|x)。大多数先前的工作使用序列的对数似然作为评估（部分）序列质量的代理。然而，最近的研究发现模型可能性与人类评估的质量之间存在差异（Stahlberg 和 Byrne，2019；Holtzman 等人，2020；Eikema 和 Aziz，2020；Zhang 等人，2021）。包括长度归一化（Wu et al., 2016）、质量感知解码（Fernandes et al., 2022）和正则化解码（Meister et al., 2020a）在内的各种方法都试图修改目标以缩小差距。在这项工作中，我们采用h(·)作为评分函数，h(y1…t)是假设y1…t的得分。

图表符号 我们将序列的推导视为有向搜索图的扩展，其中 BOS 是根节点，EOS 节点是叶节点。除根节点外，任何节点 n 都只有一个父节点。每个节点n的得分被定义为以BOS开始并以n结束的假设的得分。 h(·) 抽象出任何评分函数。每个节点 n 可以表示为一个三元组 <s, w, t>，其中分数为 s = h(n)，令牌 w ∈ V 是生成的令牌，t 是发现时间。完整序列定义为 ? y = (BOS, · · · , EOS)，并且 ? Y 由所有完整序列组成。图的开集O，也称为搜索前沿，本质上是一个优先级队列3。

最佳优先搜索
最佳优先搜索（BFS）是一种贪婪搜索算法，它根据评分函数 h(·) 来探索图。我们在算法 1 中描述了概率 NLG 背景下的最佳优先搜索算法。对于每次迭代，BFS 都会找到最有希望的节点，对其进行扩展，将新发现的节点添加到 O 中，然后重复直到达到预算。 is-complete 是终止的条件函数。 P 包含完整的序列。 T 计算已探索节点的数量。尽管BFS已经在很多领域得到应用NLP 应用（Och 等人，2001；Klein 和 Manning，2003；Bostrom 等人，2022；Saha 等人，2022），它并不是文本生成的流行选择。最近在解码策略方面的工作（Meister et al., 2020b; Lu et al., 2022; Xu et al., 2022）受到了BFS的启发和推动，但都没有直接采用BFS作为解码算法。

2.1优势

与波束搜索和采样方法相比，使用 BFS 的潜在优势是什么？我们在表 1 中列举了波束搜索、采样和最佳优先搜索的固有属性。BFS 有很多优势可以满足文本生成中的多样性、质量和可控性等所需属性。

确定性的 BFS是一种确定性搜索算法，比随机采样方法具有更低的方差和更高的可控性。这也表明BFS兼容采样op，类似于集束搜索。

无重复 BFS 没有重复，因此可以保证使用的搜索预算越多，独特的输出就越多。截断阈值低的采样方法会遇到这个问题。

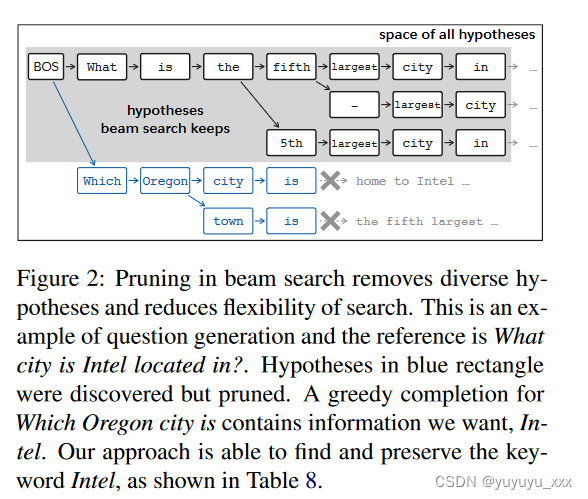
无剪枝 我们在图 2 中说明了集束搜索中的剪枝问题。BS 剪枝了所需的假设。与波束搜索不同，BFS 从不修剪5，并保留所有探索过的节点。这也带来了很大的灵活性，一代人可以在不同的搜索分支之间切换。
多样性 BFS 产生质量不错的多样化输出。生成序列的多样性基于经验透镜，这将在我们的实验中涵盖。

2.2 挑战

正如我们已经讨论了 BFS 所具有的许多优势，为什么它没有成为主导方法呢？我们实现了标准最佳优先搜索算法（如算法 1 中所述），并研究了它如何解码 BART-XSum6 中的文本摘要。我们还定义了等效光束尺寸的概念7来校准所有方法的搜索预算。对于波束搜索，我们设置波束大小 b 和最大解码长度 T ，总搜索成本为 C = bT ，这意味着将有 C 次前向传递通过 LM。 BFS还可以调用LM C次并发现C个节点。

完整性 虽然波束搜索迭代地获得深度，但最佳优先搜索却没有。因此，我们调查 BFS 能够（无法）达到搜索目标（至少是一个 EOS 代币）的频率。在表 2 中，我们表明，当搜索预算非常有限时，普通 BFS 失败的可能性相当高。即使在波束大小 b = 10 的情况下，该方法也有 3% 的机会无法到达任何已完成的序列，即以 EOS 或其他预定义终止标记结尾的序列。这表明普通 BFS 在完整性方面存在困难。
效率 效率是实际使用的一个关键因素。我们测量了每个示例运行搜索所消耗的时间，并将其报告在表 2 中。作为参考，b = 10 的波束搜索可以在每个示例 0.7 秒内完成。普通 BFS 很慢，因为 BFS 中的逐步探索不是并行和批量的。

三.本文方法

我们的方法：Best-k 搜索
在本节中，我们将介绍 Best-k 搜索，这是一种受普通最佳优先搜索启发的新颖搜索算法。它具有以下几个组成部分：
（1）并行探索可以在搜索图中进行批量探索；
（2）时间衰减产生更高的完成率和更少的悬空节点；
（3）堆修剪提高了我们方法的时间和空间效率；
（4）新的评分函数，可以处理各种长度并促进多样性。我们在算法 2 中描述了该算法，并在图 3 中进行了说明。

3.1 并行探索

如表 2 所示，在类似条件下，BFS 的挂钟运行时间比波束搜索慢一个数量级。给定相同的搜索预算，理论上 BFS 应该能达到相似的时间效率。然而，当使用 GPU 时，多个分步操作实际上比批量操作慢得多。因此，我们提出了一种并行探索策略，通过每次从优先级队列中弹出 k 个节点并批量执行它们来减少探索时间成本。当前候选存储在前沿 O 中。PQ 是对 O 中的节点应用任何评分函数后的优先级队列。

其中 g = min(k, PQ.size())。该策略是最佳优先搜索的近似，因为我们不仅弹出最有希望的节点，而且还弹出前 k 个最有希望的节点。与 BFS 相比，该技术显着提高了 bestk 搜索的效率，这将在第 2 节中讨论。 5.2.
复杂性 通过并行探索，馈送到 GPU 的批次数量为 b k T 。对于波束搜索，它是 T ；对于 BFS 来说，它是 bT 。我们将每个批次的波束搜索成本设置为单位成本，这考虑了调用 LM 和其他操作。令每个批次的 best-k 搜索的额外开销成本为 ，其中考虑了填充、堆修剪、节点处理等。 best-k 搜索的时间复杂度为 Obest?k = b k T (1 + ) 其中对于 Beam搜索是 OBS = T 。值得注意的是 k 的值应该受到光束尺寸 b 的限制；否则，实际最大解码深度b k T 小于T 。在我们的实验中，当光束尺寸 b = 10 时，我们设置 k = 5 或 k = 10。

3.2 时间衰变

完成度（通过算法的输出数量来衡量）是 BFS 面临的另一个关键挑战。在表 2 中，增加搜索预算有助于提高完成率，但仍有很大一部分样本失败。我们提出了一种在搜索过程中实现完成目标的技术。对于添加到搜索边界 O 的每个节点，我们保留时间戳 t。当我们弹出节点时，我们通过添加奖励最近发现的节点的辅助分数来修改每个节点的分数。想法是增加最近发现的节点的分数，因此算法更喜欢继续它们。衰减函数必须是单调的。因此，我们将衰减函数定义为幂函数：

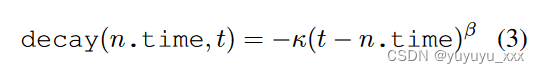
其中 κ > 0 控制项的权重，β > 0 控制斜率。 t 是当前时间步长，n.time 是过去的时间步长，因此 t ? n.time > 0。节点越旧，decay(n.time, t) 的值越小。较新的节点将从衰减函数中获得更高的激励，因此更有可能被弹出和扩展。例如，如果我们设置 κ = β = 1，则在 t = 1 时发现的节点会收到 Decay(1, 5) = ?4，而在 t = 4 时发现的节点会收到 Decay(4, 5) = ?1。实验中，我们设置β=0.5并探索不同的κ值。我们将其他形式的衰减函数（即对数）留作未来的工作。我们在附录 D 中讨论了一些竞赛设计选择。

3.3堆修剪

在探索过程中堆的大小增长得很快。然而，在大多数情况下，我们的方法仅利用排名最高的假设。时间衰减函数是单调的，因此对于搜索前沿中的任何节点，最终得分总是随着时间的推移而减小。时间衰减的使用可能会影响排名，但我们假设，如果候选节点与堆中第 k 个最高节点之间的模型得分差值大于 ，则将来不太可能使用它。边距的选择取决于因素包括时间衰减的强度、剩余搜索预算、模型校准和资源限制。在实践中，我们将最大堆大小设置为 500 足够大，以避免在不同的数据集上进行调整。
每个节点的扩展都可能导致 |V|扩展节点，其中|V|是词汇量的大小。由于条件概率 pθ(yt|y<t, x) 通常是长尾的，因此为了空间和时间效率，丢弃那些低分节点是可以的。我们设置阈值γ=0.05来过滤掉概率低于它的世代。 γ越小，我们需要实例化和管理的节点就越多。

3.4 模型得分

BFS 搜索图的深度没有对齐，而波束搜索的深度在搜索过程中保持不变。由于评分函数在寻找理想序列 ? Y 方面起着至关重要的作用，因此我们研究现有评分函数是否仍然与 best-k 搜索算法兼容。以下是定义有关（部分）序列长度 l 的评分函数 h 的几种常用方法：

原始：h(y) = Σl t=0 log pθ(yt|y<t, x)。这是用序列对数似然定义序列分数的原始方法。
长度调整评分函数：h(y) = 1 |y|α Σl t=0 log pθ(yt|y<t, x)。可调节的超参数 α 控制长度的偏好（Meister et al., 2020a）。

BFS 中的假设具有不同的长度，因此为跨样本和数据集的长度调整函数选择一个好的超参数是很棘手的。在这项工作中，我们还提出了一个无记忆评分函数：

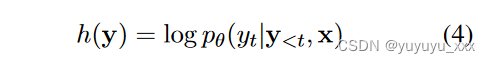
它用最后一个节点的概率来近似整个假设 y 的得分。它满足马尔可夫性质，即下一个延续只考虑最后一个状态的概率。当我们将此评分函数与 best-k 搜索一起使用时，我们将该方法称为 BKSlast 。我们进行消融研究以了解第二节中的不同评分函数。 5.3.我们发现，长度偏向的评分函数通常效果最好，而无记忆函数会生成更多样化的输出，但质量稍差。

四 实验效果

4.1数据集

我们研究了四种条件文本生成任务，范围从机器翻译等更精确的任务到常识生成和问题生成等更开放的任务。 MT 是一个并不总是需要多样化输出的用例，因此我们设计了算法，然后进行重新排名，以了解我们可以从许多多样化和高质量的输出中受益多少。我们将在第 6 节中展示机器翻译的结果
我们使用 XSum (Narayan et al., 2018) 作为抽象文本摘要的数据集。我们用于此任务的模型是在 XSum 上进行微调的 BART9 模型（Lewis 等人，2020）。最大解码长度为30。

4.2 对比模型

波束搜索（BS）是数十年来解码序列的长期选择（Reddy，1977），而多样化波束搜索是波束搜索的多样性促进变体（Vijayakumar 等人，2018）。我们尝试使用不同数量的波束组进行不同的波束搜索：5 个用于 DBS，10 个用于 DBS+。样本由两种广泛采用的强随机采样方法表示，即核采样（NCLS）（Holtzman et al., 2020）和典型采样（TYP）（Meister et al., 2022a）。波束样本包括波束搜索多项式采样方法的集合。我们尝试将波束搜索与典型采样和核采样相结合，分别表示为 BNCLS 和 BTYP。基线方法的实现可在 Transformers/GenerationMixin/generate 中找到。我们使用两种典型的配置来表示我们的方法：BKSlast（其中评分函数是无记忆的）和 BKSmean（其中 α = 1）。在 BKSmean 中，序列的得分是各个时间步的平均对数似然。我们用 k = {5, 10} 和时间衰减权重 {0.0, 0.01, 0.05, 0.1, 0.2} 进行实验，并报告具有多样性 (D) 和质量 ? 最佳组合的配置。

4.3实施细节

4.4评估指标

我们从多个方面衡量生成的输出，包括文本质量、相关性、多样性和自然度。统计 我们将已完成字符串的数量和唯一已完成字符串的数量报告为 S 和 |S|。遵循 Li 等人的多样性。 （2016）； Yang 和 Klein (2021)，我们报告了补全的独特性，以唯一 n 元语法的数量除以单词数量来衡量，表示为 D-1、D-2 和 D-3。文本质量 我们采用了两种基于相关性的度量，ROUGE (R1,R2,RL)（Lin，2004）和 METEOR (MTR)（Banerjee 和 Lavie，2005），用于评估生成的字符串和参考之间的表面相似性。自然度我们使用 MAUVE（Pillutla 等人，2021）来衡量生成序列的自然度，这是一种开放式文本生成的指标。

4.5 实验结果

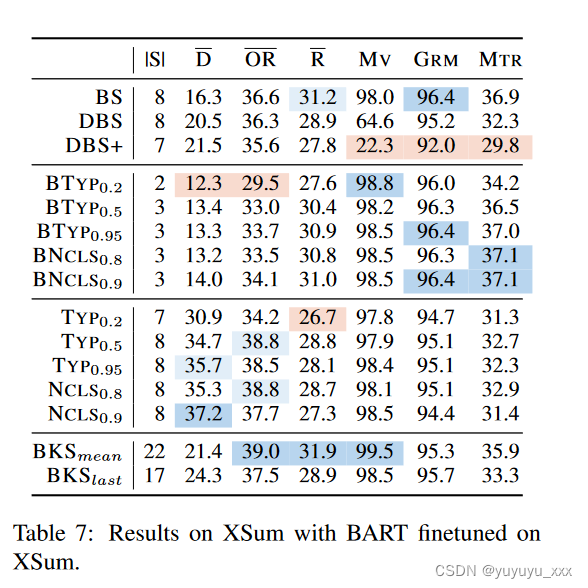
在文本摘要中，虽然只提供一种参考，但总结一篇文章的方式、风格和方面有很多种。随着对文本摘要系统输出的重新排名越来越感兴趣，生成的摘要的丰富性和多样性是值得关注的有价值的属性在。我们在表 7 中展示了文本摘要的结果。我们的方法在质量、多样性和自然性方面仍然具有竞争力。我们的方法的平均 ROUGE 为 31.9，MAUVE 为 99.5，高于任何其他方法。由于序列长度较长和悬挂节点较多，我们方法的 D 低于采样。

---

五 总结

在这项工作中，我们提出了 best-k 搜索，这是一种基于最佳优先搜索的文本生成解码算法。该算法具有一些技术组件，包括并行探索、时间衰减和堆修剪。所提出的算法生成自然且多样化的文本，同时保持高质量。我们对四个任务和六个数据集进行了全面的实验，以验证所提出方法的有效性。该算法与采样方法正交，无参数、轻量级、高效且易于使用。