密码学中的承诺原语（Commitment Scheme）

1背景介绍

让我们考虑以下情况：Alice在佳士得（Christie's）购买Banksy的最后一件杰作，在这之前，她会确保艺术品在售出后不会被销毁。

佳士得选择了维克里封闭竞标的拍卖方式，这是一种相当常见的做法，其工作原理主要是：每个参与者都提交一个秘密的竞标。一旦所有的竞标都提交完毕，出价最高的一方获得该物品，支付的价格是第二高的竞标。

承诺方案正好解决了这个问题：它们允许安全地承诺一个秘密值，并在之后打开(Open)它，以便第三方可以检查承诺是否与打开的值一致。

本文将从基本的承诺方案（如基于哈希的承诺）开始，逐步加深，并介绍目前经常使用的Pedersen和Elgamal承诺。

下一章我们将着重介绍区块链中目前正在研究的承诺方案，包括前量子安全的承诺方案，最后将给大家简单介绍一下向量承诺（Vector Commitment, VC)。

2承诺方案的定义和性质

承诺方案包括两个阶段，即承诺和公开，涉及一个确定性多项式时间算法。

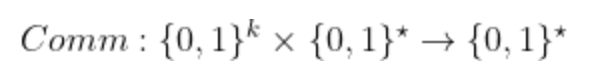
(1). 承诺阶段：在这个阶段，发送方通过计算c = Comm(u, m)将m的二进制值提交给二进制u，并将c发送给接收方，接收方将结果存储以供稍后检查。

(2). 公开阶段：在这个阶段，发送方通过与接收方共享u和m来打开c，接收方自行计算c' = Comm(u, m)并检查c' = c。

在承诺的消息是一个位的特殊情况下，我们将讨论位承诺方案。

我们需要以下属性：

(1). 它必须隐藏，意味着由Comm(u, 0)和Comm(u, 1)引起的分布是不可区分的。换句话说：Comm不透露关于m的任何信息。

(2). 它必须绑定，意味着对于任何对手，获得Comm(u, 0) = Comm(u', 1)的概率在两个随机二进制u和u'上是可以忽略的。这意味着发送方输出一个提交，后来可以打开为两个不同的消息是不可行的。

如果对手受限于概率多项式时间算法，则承诺方案被称为计算隐藏或绑定，否则，该方案将被称为完全隐藏或绑定。

拥有既完全绑定又隐藏的承诺方案是非常困难的，因为想象一下承诺方案是信息理论上绑定的，意味着找不到随机二进制u和u'使得：

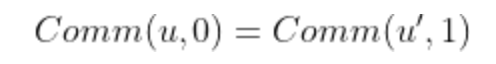
否则，发送方将能够计算出u和u'，并随意打开承诺。然而，如果发送方通过计算c = Comm(u, 0)来承诺0，接收方将会通过穷举法发现没有u'使得c = Comm(u', 1)，因此接收方将知道承诺的位是0，该方案将不具备隐藏性。

3预备知识

如果遵循以下两个方法，我们可以很容易地创建承诺方案，其优点在于创建高效且具有良好隐藏和绑定特性的方案。

创建承诺方案的一种方法是使用抗碰撞哈希函数H，并定义一个计算上绑定和隐藏的承诺方案，具体如下：

1. 通过设置c = Comm(u, m) = H(u||m)对任何消息m进行承诺。

2. 通过揭示(u, m)并检查等式c = H(u||m)是否成立来打开承诺。

另一种创建承诺方案的方法是使用对称或非对称的加密系统，即：在这种方案中，我们生成公钥和私钥对(sk, pk)，然后删除私钥sk（出于安全考虑，否则我们可以简单地解密承诺的值）。

为了承诺一个值m，用户会抽样一些随机参数r并输出。

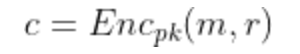
要打开承诺c，我们会揭示（m，r）并检查。
?

4常用的承诺--Pedersen? 和 Elgamal

这是密码学中一个活跃的话题，尤其在区块链技术和保密交易中被证明特别有用。我们可以找到几种常用的承诺方案，包括Damgard-Groth承诺、Gennaro承诺、MacKenzie-Yang方案、Galindo-Garcia-Van Rossum承诺和Naor承诺。

然而，我们关注两个在区块链中特别常用的承诺方案：Pedersen承诺和Elgamal承诺（文献中也拼写为ElGamal）。

Pedersen承诺

在这个承诺方案中，我们有以下设置：假设q是一个素数，G是一个阶为q的循环群，有两个生成元g和y。

为了承诺于m ∈ Zq，发送者选择均匀随机元素r ∈ Zq，并输出

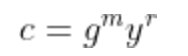
为了打开一个承诺c，发送者揭示对(m, r)。如果接收者接受对m的打开，则满足条件

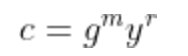
观察到，如果群G在离散对数假设下是安全的，那么这个承诺是完美隐藏的且计算上绑定的。

Elgamal承诺

在这种情况下，假设和Pedersen承诺一样，G是一个循环群的素数阶q，并且给定两个生成元g和y。

为了承诺于一个元素m ∈ G，随机选择r ∈ Zq，并计算

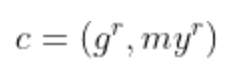
为了打开一个承诺c，发送者揭示对(m, r)。如果接收者接受对m的打开，则满足条件

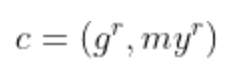
我们观察到Elgamal承诺承诺于G的元素，而Pedersen承诺承诺于Zq的元素。关于性质，Elgamal承诺是完美绑定的但计算上隐藏的。

5
?

总结

我们主要介绍了承诺方案（Commitment Scheme）的定义，随后通过一个简单的基于哈希函数的承诺方案，简单介绍了一下承诺方案需要满足的几个性质，最后介绍了一下区块链中常用的两种方案，Pedersen和Elgamal承诺。

5开关承诺（Switch Commitment）

我们有一个完全隐藏且计算上绑定的承诺方案，还有另一种实现计算上隐藏且完全绑定的方案。此外，这两种方案虽然都非常高效，但是将它们组合起来不能得到一个完全隐藏和绑定的方案（记住：你不能拥有一切）。

我们可以尝试构造一个在某个时刻完全隐藏且在某个时刻完全绑定的方案。这个方案就是所谓的开关承诺 (Switch Commitment)：Pedersen和Elgamal承诺的结合。

开关承诺与范围证明的结合，在涉及机密交易的加密货币中起着重要作用，并且对试图危及离散对数安全性的攻击具有抗量子性。

开关承诺由四个算法组成：

1. 给定安全参数作为输入，设置算法输出一个公共随机字符串。

2. 给定公共随机字符串和消息作为输入，承诺算法输出一个承诺和开启信息。

3. 给定与承诺相关联的部分开启信息，部分验证算法输出1。

4. 给定与承诺相关联的完整开启信息，完整验证算法输出1。

与此同时，开关承诺必须满足以下要求：

1. 承诺算法是计算上隐藏的。

2. 部分验证算法是计算上绑定的。

3. 完整验证算法是完全绑定的。

在我们的设定中：

1. 算法Setup(l, d)初始化一个素数阶q的乘法群G，随机选择生成元g和y，并输出crs = (G, g, y, d)。

2. 承诺算法Comm(crs, m)随机选择r ∈ Zq，并输出一对

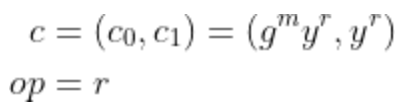
3. 部分验证算法VerifyP(crs, c, op, m)如果返回1，则说明

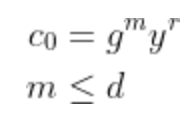
4. 完整验证算法VerifyF(crs, c, op, m)如果返回1，则说明

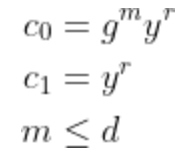
有人认为存储Elgamal组件可能会引入不必要的存储开销。我们可以通过设置

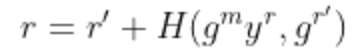
对于某个哈希函数H和一个随机的r’ ∈ Zq，然后定义

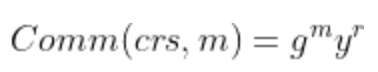
这个技巧允许我们将Elgamal承诺封装到Pedersen的承诺中。在这种情况下，op = r’，部分验证检查是否

开关承诺与范围证明结合在涉及机密交易的加密货币中起着重要作用，并且对试图危及离散对数安全性的攻击具有抗量子性。

6关于后量子方案的提案

一些作者一直在探索抗量子的承诺方案。在这个方向上，我们要强调Benhamouda、Krenn、Lyubashevsky和Pietrzak所做的工作，他们设计了一种基于环问题的学习与错误的困难度的高效承诺方案，以及一个零知识证明。

还有其他基于格难题的构造，比如Jain等人提出的方案，其隐藏性质基于学习带噪音的奇偶校验问题（LPN）。LPN是q = 2的学习与错误问题。

Baum等人提出了一个基于结构化格难题的可加同态承诺方案的实际构造，以及一个开启知识的零知识证明。他们的方案在设计上改进了之前Benhamouda等人的工作，因为它不仅限于完全绑定。虽然可以将他们的方案实例化为完全绑定或完全隐藏，但当隐藏和绑定属性只是计算上时，它最高效。

7向量承诺（Vector Commitment）

格不仅仅被用来定义抗量子的承诺方案，短整数解问题也可以提出相关有趣的承诺方案：向量承诺。

向量承诺允许简洁地承诺一个有序序列的值，以便后续可以简洁地证明所需位置上的值，即：给定一个承诺的d维向量m，我们可以证明m[i]恰好是m的第i个条目。

在这种情况下，binding是通过位置绑定完成的，这意味着在位置i打开承诺作为两个不同的消息条目m[i]和m'[i]是不可行的。对于隐藏性，我们要求位置隐藏，这意味着承诺和开放不会透露有关未打开的消息条目的任何信息。

假设消息空间M、承诺空间C和证明空间P，向量承诺方案由以下算法构成：

1. Setup(l, d) 输出公共交通参数cp和验证器参数vp。

2. Comm(cp, m) 接受d维消息m，并输出承诺c以及承诺者状态st。

3. Open(cp, st, i∈[d]) 输出与st相关的承诺消息的第i个条目的证明pi ∈ P。

4. Verify(vp, c, m[i], pi) 输出1或0。

这些算法必须满足以下正确性条件：

对于任何d维m，i ∈ [d]，(cp, vp) = Setup(l, d)，(c, st) = Comm(cp, m)和proof pi = Open(cp, st, i)，验证算法Verify(vp, c, i, m[i], pi)以可忽略的概率输出0。

向量承诺方案的安全性依赖于（齐次）短整数解问题的困难程度，该问题要求给定一个均匀随机的（n x m）-矩阵A，其系数在Zq中，找到一个非零整数m-向量z，使得Az ≡ 0（mod q）且║z║< n，其中n> 0。

总结

在这篇文章中，我们介绍了主要的概念和技术，希望能帮助读者了解并跟进区块链框架中正在进行的研究。

那些耐心读完这篇文章的人应该对Pedersen和Elgamal承诺的工作原理有一个清晰的理解，因此他们将能够理解保密交易的核心部分。

关于向量承诺，我们希望能够传达主要的思想，这应该是深入研究该领域及其在空间证明协议设计中应用的良好起点。