模型稳定性评估 简介
发布时间:2023年12月25日
OOT
OOT(Out of Time)是在建模过程中用于描述模型在时间维度上的性能变化的术语。当模型在训练时使用的数据集与实际应用场景中的数据分布发生差异,特别是在时间上存在间隔时,就可能出现OOT问题。
OOT通常指的是模型在训练时使用的数据集与将来要在实际应用中使用的数据集有显著的时间差异,导致模型在未来的预测性能下降。这种情况可能由于数据的时效性、外部环境的变化等原因引起。
解决OOT问题的一种常见方法是使用群体稳定性指数(Population Stability Index,PSI)等工具来监测模型在不同时间段或数据分布上的性能变化。通过在模型上线前和上线后对模型性能进行监测,可以及时发现潜在的OOT问题并进行调整。
预防OOT问题的方法包括:
- 及时更新训练数据: 确保模型的训练数据集包含最新的信息,以适应未来的数据分布。
- 动态更新模型: 考虑使用增量学习或定期重新训练模型,以捕捉潜在的数据分布变化。
- 监测模型性能: 定期监测模型在不同时间点或数据分布上的性能,使用PSI等指标进行评估。
通过这些方法,可以提高模型对未来数据的适应能力,减少由于时间上的变化而导致的性能下降问题。
PSI
PSI 指标就是群体稳定性指数(Population Stability Index)
通过 PSI 指标,可以得到不同样本(不同时间段给到模型的样本)下,模型在各分数段分布的稳定性。
用于衡量两个群体(比如两个时间点、两个子群体等)之间稳定性的指标。通常,PSI被广泛用于评估信用风险模型、预测模型等在不同时间点或不同群体中的性能变化。
PSI = SUM ( 实际占比 - 预期占比 ) * ln ( 实际占比 / 预期占比 )
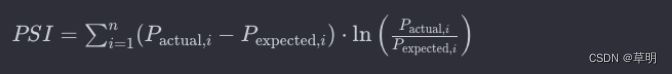
P actual,i- 表示实际分布中第i个分箱的占比P expected,i- 表示期望分布中第i个分享的占比
通常,期望分布可以是参考的基准分布,比如在时间点1的分布作为基准,而实际分布是在时间点2的分布。
结果:
- PSI的值越大,表示两个群体之间的分布差异越大
通常,一些经验性的阈值可以用来解释PSI的结果,比如:
PSI<0.1: 稳定性很高0.1≤PSI<0.25: 稳定性一般PSI≥0.25: 稳定性较差
稳定性是一个相对的概念,只有通过对比,才能知道模型是不是稳定。所以,想要计算模型的稳定性,需要先有一个参照物。
在信用评分模型中,为了进行对比,至少需要两个分布结果,一个是预期分布结果一个是实际分布结果。
流程:
- 在模型验收前, 算法工程师需要对模型的稳定性进行评估.
- 使用验证样本作为实际分布,
- 使用训练样本作为预期分布
- 在产品验收阶段, 产品经理
- 使用模型上线时的 OOT 样本作为预期样本
- 使用 非 OOT 时段的近期抽样样本作为实际样本
计算 PSI
- 分箱
- 等频分箱
- 每个分箱中的样本数量相等,分数段不同,并且分数段是根据人数占比计算得到的
- 等距分箱
- 每个分箱中分数段相同,人数不同,人数是按照分数平均切分的
- 等频分箱
- 计算实际分布
- 测试样本距离当前日期越近越好
- 选择进行测试的样本,把样本传入模型得到实际测试结果
- 再根据上一步选择的分箱方式,将实际测试结果同样进行分箱,计算分箱后的占比
- 计算 PSI 数值
实际占比 - 预期占比实际占比 / 预期占比ln(实际占比 / 预期占比)index = (实际占比 - 预期占比) * ln(实际占比 / 预期占比)PSI = sum(index1 + index2 + ...+ indexn)
建议
- PSI 上线时关注, 上线后也要持续关注
- 关注 PSI 变化因素
- 客群变化
- 数据源变化
- 上线后, 根据业务场景对模型稳定性的要求, 对模型 PSI 进行按日 / 按月 / 按季度监控
文章来源:https://blog.csdn.net/galoiszhou/article/details/135196663
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【目标检测】YOLOv5算法实现(八):模型验证
- 2023-12-29 工作心得补充 适时抽取方法,让代码变简洁
- 鸿蒙开发之图片下载
- 专业粉碎文件,数据安全与销毁:数据销毁实践指南
- k Nearest Neighbour(KNN)建模
- 《微机原理》考试全真模拟卷带解析
- 【K8S in Action】第七章 ConfigMap和Secret配置应用程序
- 【网络安全】SQL注入总结
- AI变现项目:刚做五天收益突破单日破50+,干货经验谈
- 鸿蒙Web组件_学习