快速排序：高效分割与递归，排序领域的王者算法

🎬 鸽芷咕：个人主页
?🔥 个人专栏: 《数据结构&算法》《粉丝福利》

??生活的理想，就是为了理想的生活!

---

📋 前言

快速排序这个名词，快排之所以叫快排肯定是有点东西的。他在处理大规模数据集时表现及其出色。其思想是在Hoare于1962年提出的一种二叉树结构的交换排序方法，利用了二叉树的思想来构建排序。

一、快速排序的介绍

快速排序是一种基于分治思想的高效排序算法，由Tony Hoare于1960年提出。它的核心思想是通过选择一个基准元素，将数组划分成两个子数组，使得左边的子数组元素都小于基准，右边的子数组元素都大于基准，然后对这两个子数组分别进行递归排序。

二、快速排序的实现

快速排序是一种基于分治思想的高效排序算法其核心就是每次找到最中间的位置然后再进行递归继续找到最中间的位置然后再分割一直分割到只剩一个数的时候那么这个数组就是有序了。

• 🔥 注：这里红色代表中间值。
• 每次找到中间值之后利用分治思想，大问题化为小问题
• 然后递归进行排序当递归完成时每个中间值都找到就是排序好的时候

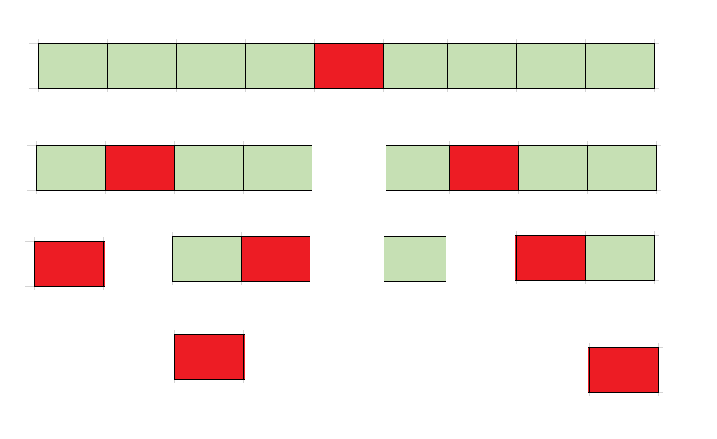
而要搞定一个排序首先最先解决的就是其中单趟排序下面就是各位大佬想出来的单趟排序方法：

• 先把部分的单趟排序搞出来后面来实现整体排序就简单多了

2.1 hoare版本

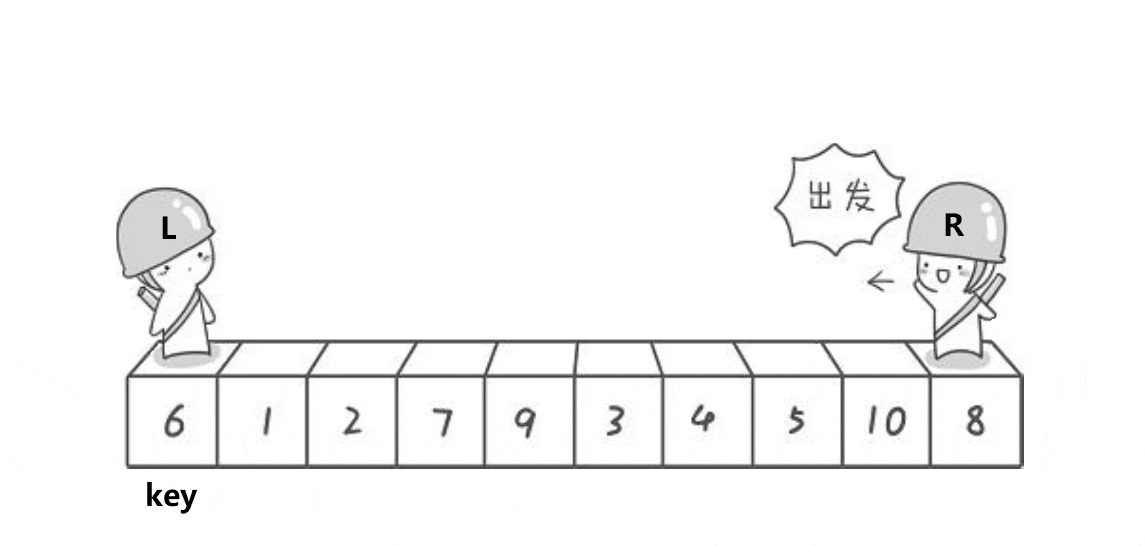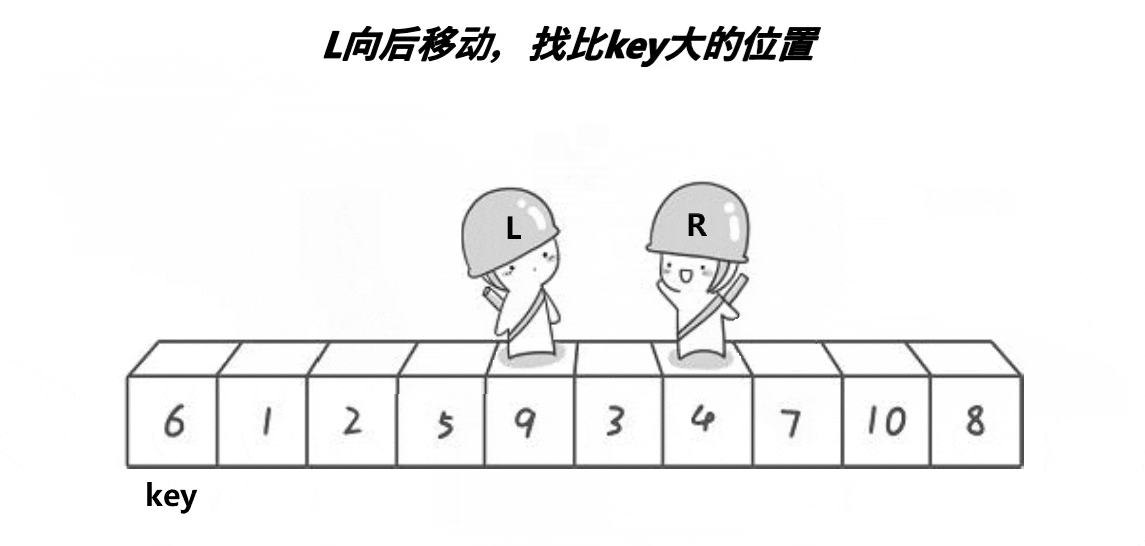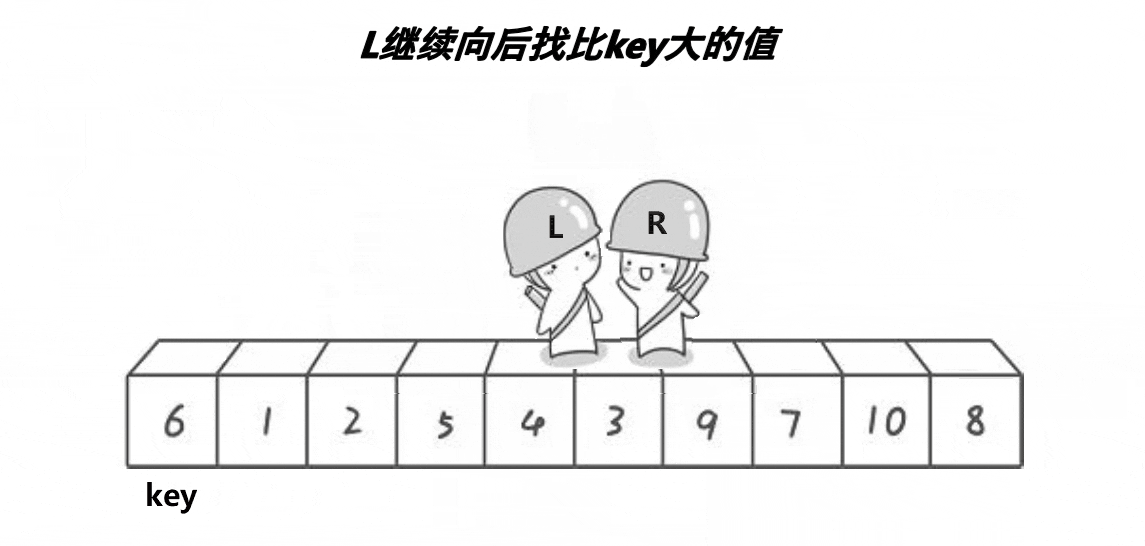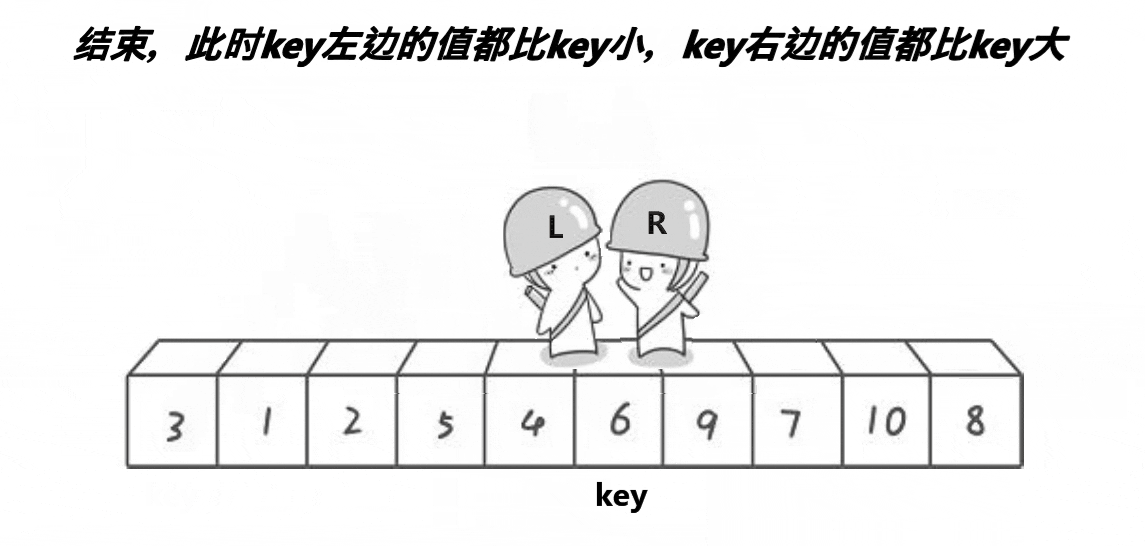
hoare版本的方法就是那 key 选择作为中间值，然后用left 当做最左边的下标 right 当做最右边的下标

• 每次right 先走去找比 key 值要小的数，找到了就停下来
• 然后left 在走去找比 key 值要大的数，找到了之后 left 和 right 的值进行交换

一直重复下去直到他俩相遇的时候就是找到中间值的位置了了，然后把 key 这个中间值和 left 或者 right 交换到中间值的位置

🍸 代码演示：

//hoare法排序
int PartSort1(int* a, int left, int right)
{

	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[right], &a[left]);
	}

	Swap(&a[keyi], &a[left]);

	return left;
}

为什么每次相遇位置都比key要小

1. 因为每次都是 right 先走所以是 R 先找到比可key 小的

这时就有俩总情况了分别是 R 不动 left 走
他俩相遇

• 由于R已经找到了比key要小了，所以当他们相遇和 key 交换时 相遇位置都比key要小

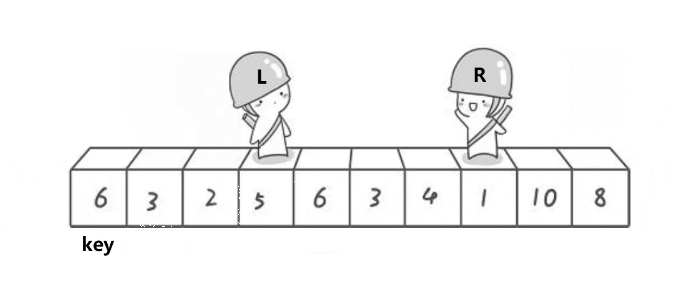
或者 R 和 L 交换完成之后 L 就是最小的了，这时是 L 不动 R 先走

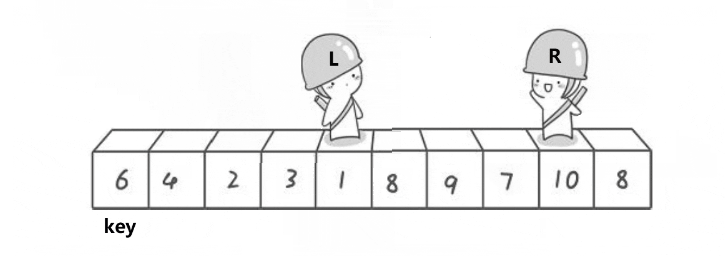
2.2 挖坑法

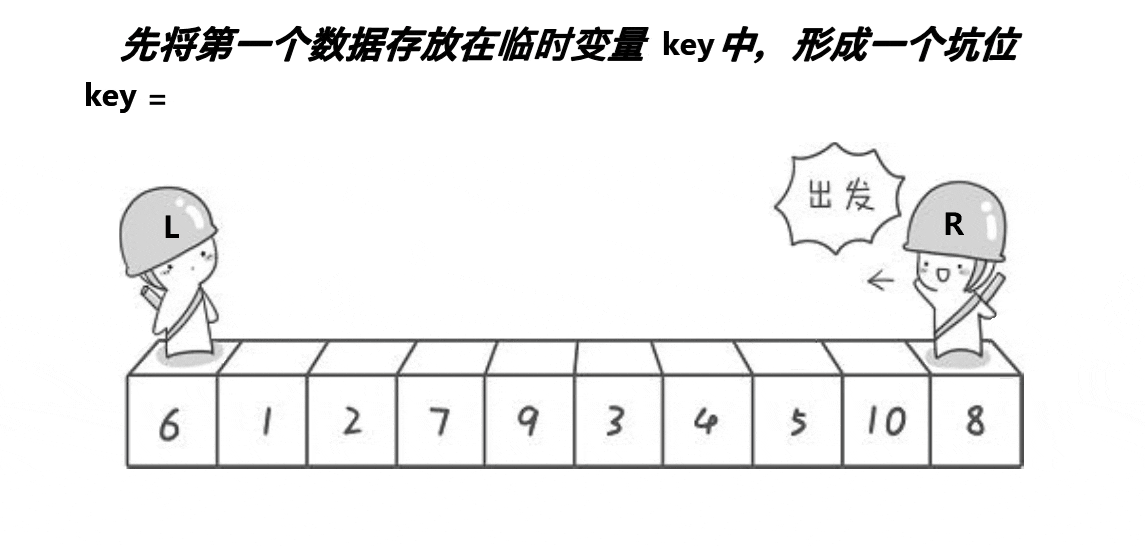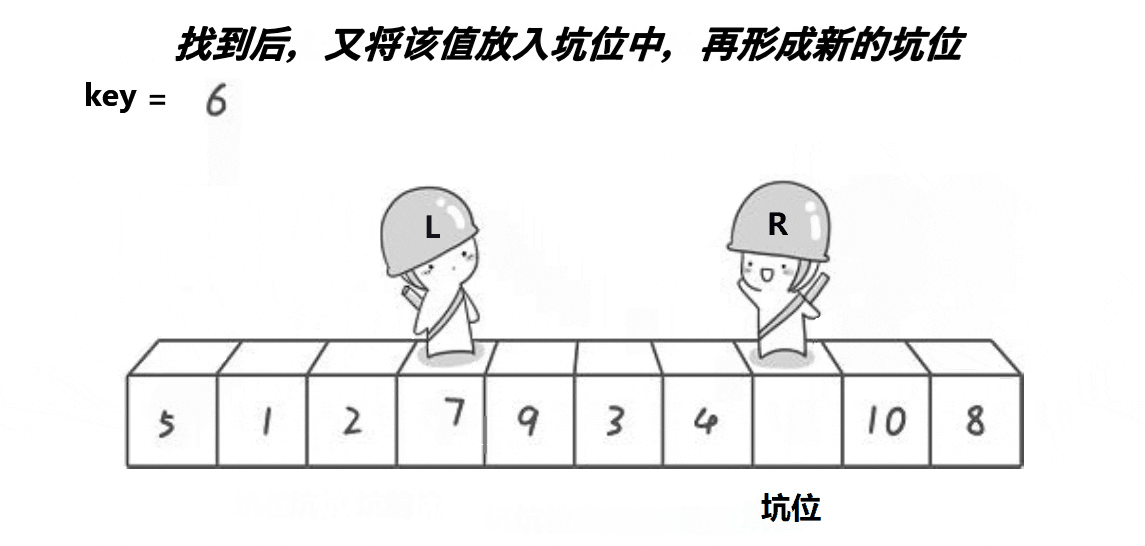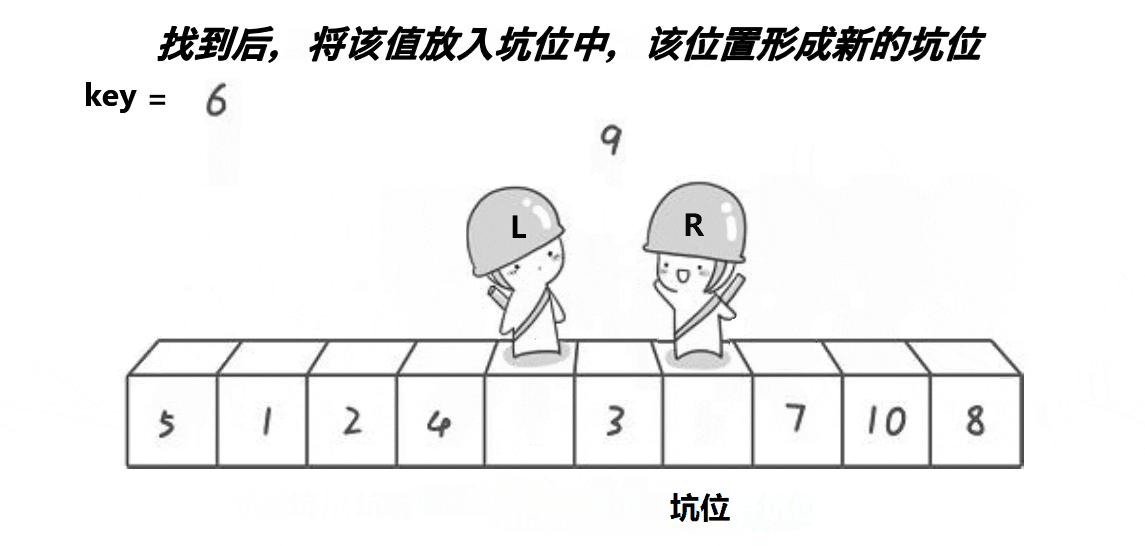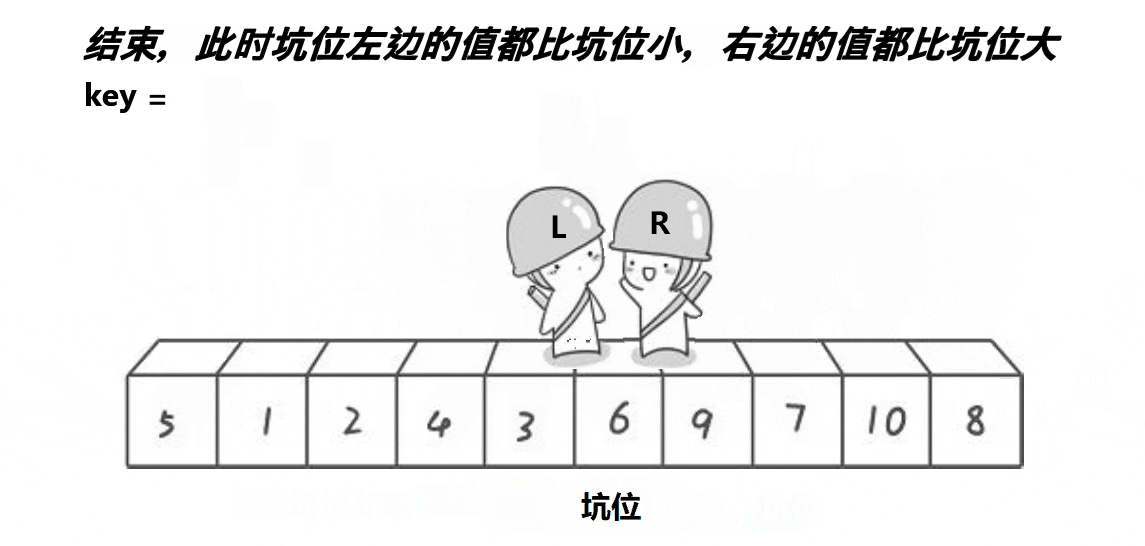
有人呢觉得hoare 大佬的方法单趟排序太麻烦了每次控制好左右，所以就提出改进了 hoare 的排序方法命名为挖坑法

简单点来讲 key 用来记录第一个值，然后把它的下标记下来 当做第一个坑位

• 然后 right 向前找找到比 key 的值小的时候就和 left 交换 并且把 hole 坑位给记录为新的位置
• 然后 left 向前走，找到比 key 值要大的时候 和 right 交换 并记录下新的坑位 hole

🍸 代码演示：

//快速排序挖坑法
int PartSort2(int* a, int begin, int end)
{
	//三数取中
	int midi = GetMidi(a, begin, end);
	Swap(&a[begin], &a[midi]);

	//保存第一个坑位的值
	int key = a[begin];
	//每个坑位的下标用于交换数据
	int hole = begin;

	while (begin < end)
	{
		while (begin < end && a[end] >= a[hole])
		{
			end--;
		}
		Swap(&a[end], &a[hole]);
		hole = end;

		while (begin < end && a[begin] <= a[hole])
		{
			begin++;
		}
		Swap(&a[begin], &a[hole]);
		hole = begin;
	}
	
	a[hole] = key;
	return begin;

}

2.3 前后指针版本

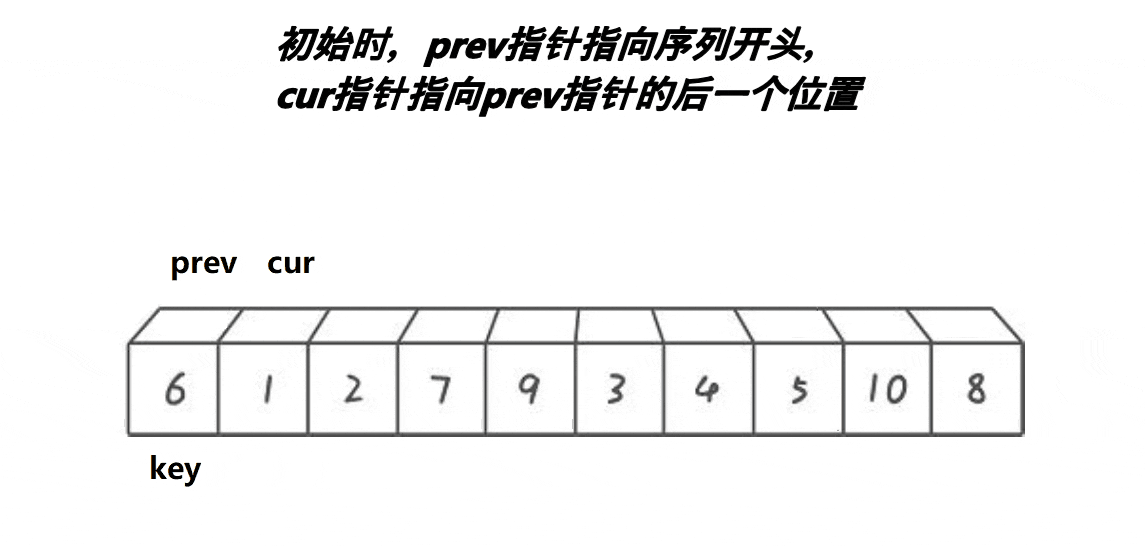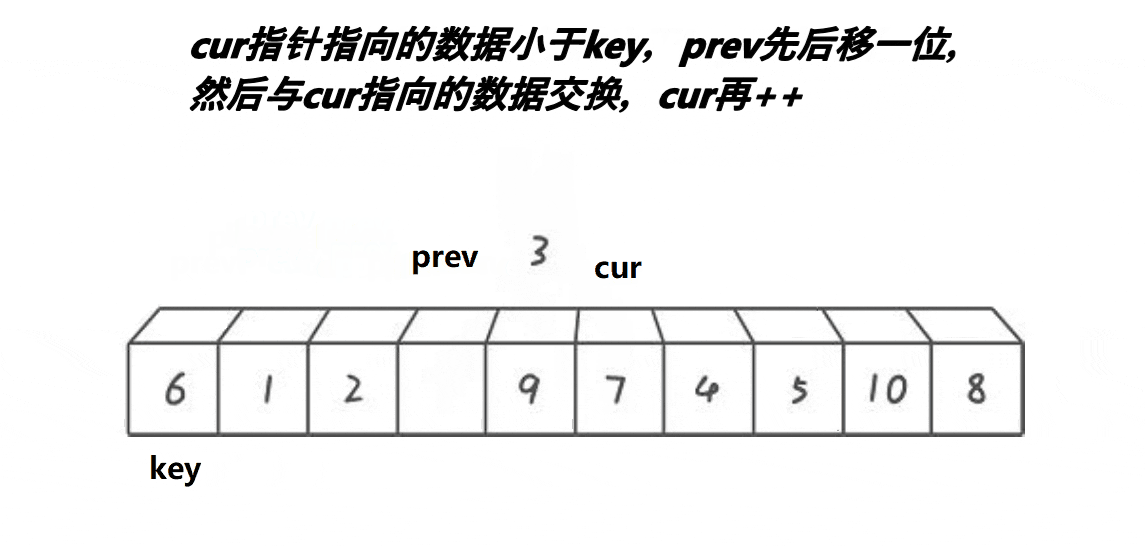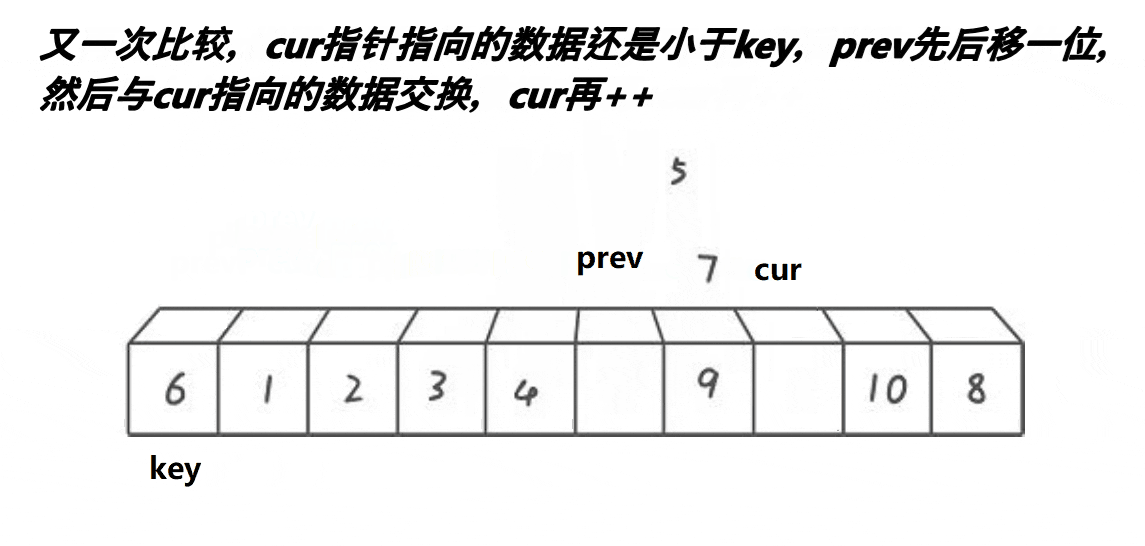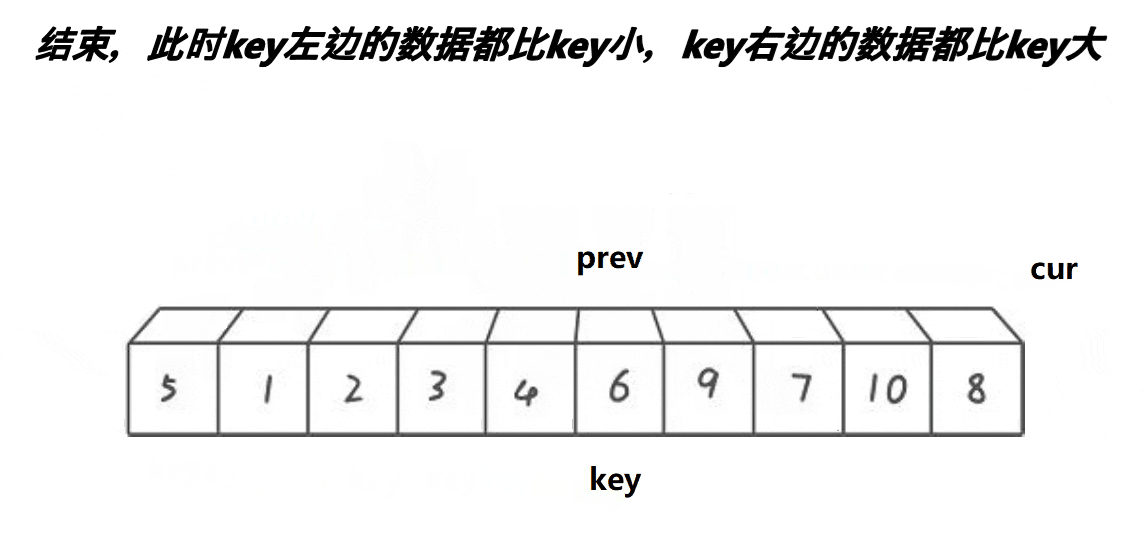
时至今日诶有些人还是觉得前面俩种方法太麻烦了，为什么一定要右边先走所以就有了第三种方法前后指针法大大优化了快排的方法。

这里的核心思想是还是一样，key是我们需要进行比较的中间值

• prve 指针初始化的位置为 begin 的位置
• cur 指针初始化为 prve + 1 的位置

然后每次 cur的值和 key 的值做比较 如果小于 key 那么 prve 就+1 ， cur 和 prve 交换位置

• cur 继续向前走一步 如果 cur 的值比 key大的话就继续++ ， prve 不动这样一直循环下去

注：当循环结束的时候也就是 cur > end 数组长度的时候，就吧 cur 和 key 交换值，这样中间值就到了我们预想的位置

//前后指针法
int PartSort3(int* a, int begin, int end)
{
	int prve = begin;
	int cur = prve + 1;
	int keyi = begin;

	while (cur <= end)
	{
		if (a[cur] < a[keyi] && prve++ != cur)
		{
			Swap(&a[prve], &a[cur]);
		}
		cur++;
	}

	if (cur > end)
	{
		Swap(&a[keyi], &a[prve]);
	}
	return prve;
}

三、快速排序的优化

快排的最坏情况

快速排序虽然很快时间复杂度一眼看上去都是 N*longN 但这只是最好的情况：

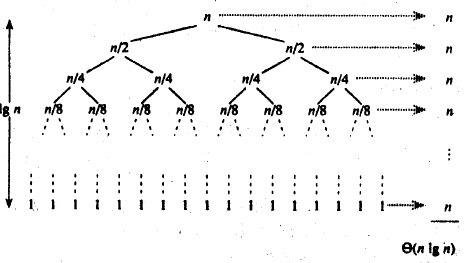
🔥 注：最坏的情况复杂度是 N*N，每次 key 选的值都是最小的

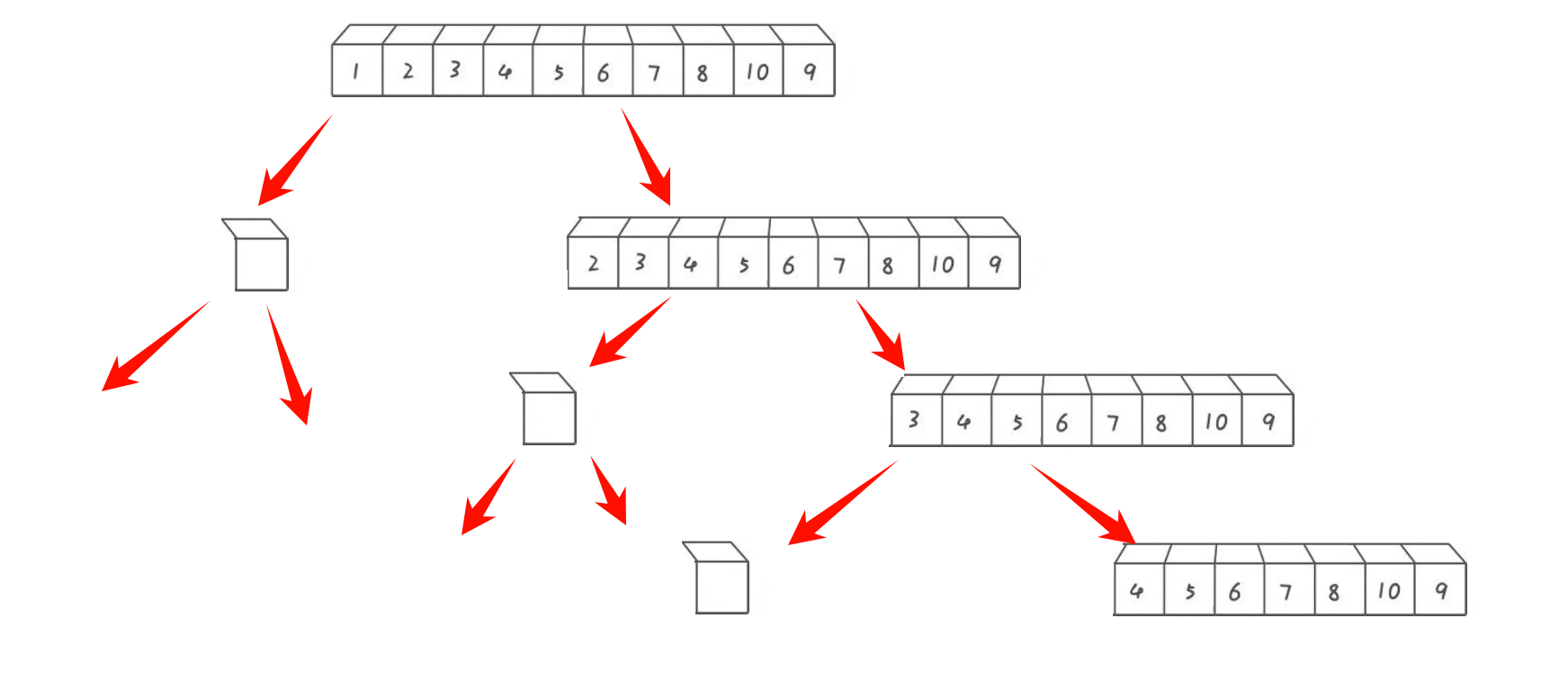
每次进行递归并不是完全二叉树的样子，每次都需要全部遍历一遍才找到一个数据

• 所以就有了三数取中这个算法

3.1 三数取中

顾名思义，三数取中就是把，left 和 mid right 里面找到一个中间数的下标来进行返回

• 然后再把 left 和 mid 来进行交换这个每次 key 取值都是靠近中间数

这样就完美解决了二叉树的最差情况使得效率大大提升

🍸 代码演示：

//三数取中
int GetMidi(int* a, int left, int right)
{
	int midi = (left + right) / 2;

	if (a[left] < a[midi])
	{
		//a[left] < a[midi] <a[right]
		if (a[midi] < a[right])
		{
			return midi;
		}
		//a[left] < a[right] < a[midi]
		else if (a[midi] > a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else
	{
		//a[left] > a[midi] > a[left]
		if (a[midi] > a[left])
		{
			return left;
		}
		//
		else if (a[midi] < a[left])
		{
			return midi;
		}
		else
		{
			return right;
		}

	}
}

3.2 递归到小的子区间时使用插入排序

快排的最坏情况我们优化了，但是其实还有一个优化方法，现在我们知道了快排是利用二叉树的思想但是二叉树的递归的弊端就是栈的太大了：

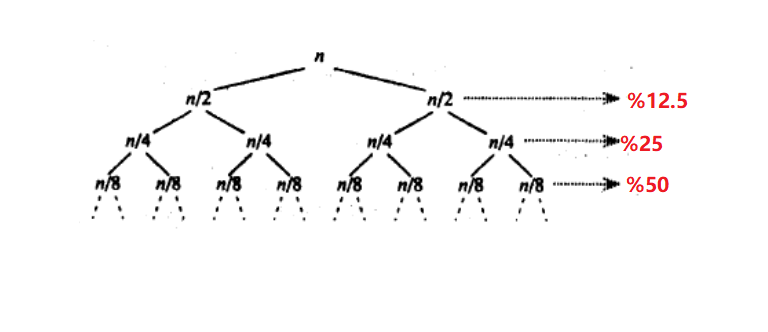
• 而二叉树的叶子节点就占了整课树的 %50 假如我们在 递归区间只有10的时候就使用插入排序呢？

因为如果有很多的数据进行排序的话 快排的特性是每次到找到中间值然后再递归所以但递归到了10这个区间的时候就大致有序了，而插入排序对有序数组排序最快是 O(N)

• 所以我们选择当区间为 10 的时候采用插入排序来进行排序

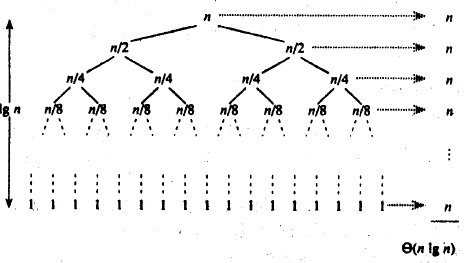
🔥 那么这样的递归栈消耗可以减少多少呢？

这里就可以看到递归的栈区消耗优化达到了惊人 %80

🍸 代码演示：

//快速排序
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;

	if ((end - begin) > 10)
	{
		int div = PartSort3(a, begin, end);
		QuickSort(a, begin, div - 1);
		QuickSort(a, div + 1, end);
	}
	else
	{
		InsertSort(a+begin, end-begin+1);
	}
}

3.3 快速排序的最终代码

好了所以关于快排的方法我们讲完了，下面就来看看最终的快排代码吧！

//快速排序
void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;


	if ((end - begin) > 10)
	{
		//三数取中
		int midi = GetMidi(a, begin, end);
		Swap(&a[begin], &a[midi]);

		int prve = begin;
		int cur = prve + 1;
		int keyi = begin;

		while (cur <= end)
		{
			if (a[cur] < a[keyi] && prve++ != cur)
			{
				Swap(&a[prve], &a[cur]);
			}
			cur++;
		}

		if (cur > end)
		{
			Swap(&a[keyi], &a[prve]);
		}
		QuickSort(a, begin, prve - 1);
		QuickSort(a, prve + 1, end);
	}
	else
	{
		InsertSort(a+begin, end-begin+1);
	}
}

四、快速排序的总结

快速排序的特性总结：

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(logN)

4. 稳定性：不稳定