定点数、浮点数和浮点数计算方式

目录

一、定点数、浮点数定义

1、定点数

2、浮点数

二、IEEE754单精度浮点数计算

概要

? ? ? ?在计算机中,通常是用定点数来表示整数和纯小数,分别称为定点整数和定点小数。对于既有整数部分、又有小数部分的数，一般用浮点数表示。下面分别予以介绍:

一、定点数、浮点数定义

1、定点数

????????定点数是一种表示固定小数位数的数值类型，通常表示为一个有符号的整数部分和一个小数部分。

????????定点小数：如果是有符号数，约定小数点在符号位的后面，如果是无符号数，约定小数点在最前边。 定点小数的是类似：0.XXXXXX这个形式

????????定点整数：约定小数点在最后边。定点整数是类似：XXXXXX.0这种形式

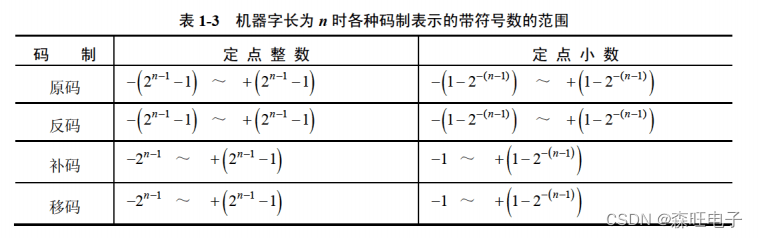
????????设机器字长为n，各种码制表示下的带符号数的范围。

2、浮点数

????????浮点数是小数点位置不固定的数，浮点表示法能表示更大范围的数。

????????一个含小数点的二进制数N可以表示为更一般的形式：

????????????????????????????????????????????????????????????N=2 ^E×F

????????其中，E称为阶码，F为尾数，这种表示方法称为浮点表示法。

????????在浮点表示法中，阶码通常为带符号的纯整数，尾数为带符号的纯小数。浮点数的表示格式一般如下：

工业标准IEEE754

????????IEEE 754是由IEEE制定的有关浮点数的工业标准，被广泛采用。

????????IEEE754标准提供了两种规格的浮点格式：32位单精度格式和64位双精度格式。

???????

? ? ? ? 符号位：1表示负数，0表示正数

????????阶码：用移码表示，偏置常数为2^( n ? 1) ? 1 。

????????尾数：用原码表示。尾数分为规格化尾数和非规格化尾数

? ? ? ? 规格化尾数：对于非0的值，尾数的最高位必须是1，这也就避免了相同的数字可以使用不同的表达。因为最高位始终是1，所以这个1就不需要存储了，这样实际就使用23位存储了24位尾数的效果，扩大了1位精度。

? ? ? ? 非规格化尾数：尾数的最高位是0。如果运算后，结果小于最小的规格化数，那么会下溢，这时候就使用非规格化数表示，对于非规格化数，真实的指数可不是-127，而是-126，

-127被0使用了，这个就是一个约定。计算机处理浮点数的时候，如果发现指数部分是0，尾数不是0的，就会直接使用-126作为真实的指数。

? ? ? ? 注：移码指数是0，尾数也都是0，代表0。

???????????????移码指数都是1，尾数都是0，代表无穷大。通过符号位可以有+∞和-∞

二、IEEE754单精度浮点数计算

例1：将13.25转成IEEE32位规格化二进制

计算步骤：

1. 先确定符号位：0
2. 将十进制小数转成二进制小数：1101.01
3. 移动小数点，尾数规格化：1.10101，尾数最高位1隐藏，存储尾数是10101
4. 尾数规格化对应的指数为+3，移码指数：3+127=130， 对应的二进制：10000010
5. 根据上面的信息构造浮点数的IEEE754 表示法为：

0 10000010 10101000000000000000000

例2：将100.6785转化IEEE32位规格化二级制?

计算步骤

十进制数表示方法： 100.6785D 末尾加D
二进制数表示方法： 1100100.1010B 末尾加B (默认保存四位数，如果小数位都是0，那么就取直到不为0的位数)
计算过程：
第一步：把十进制数转换为二进制数
  100.6785D
= 1100100.1010B

第二步：用二进制的科学计数法表示
  100.6785D
= 1100100.1010B
= 1.1001001010 x 2^6

第三步：计算出E的值
6 = e = E - 127
所以：E = 133D = 1000 0101B

第四步：组合
S：0 表示正数 1 表示负数
E：1000 0110
M：1001 0010 1000 0000 0000 000 （取小数点后的数值，小数点前为隐含位，共23位）

所以：100.6785D的标准单精度浮点数是 0 1000 0110 1001 0010 1000 0000 0000 000