Modeling Long- and Short-Term Temporal Patterns with DeepNeural Networks

发布时间：2023年12月26日

This paper was pulished at?SIGIR’18, July 2018, Ann Arbor, MI, USA

一、简介

LSTNet是一种用于时间序列预测的深度学习模型，其全称为Long- and Short-term Time-series Networks。LSTNet结合了长短期记忆网络（LSTM）和一维卷积神经网络（1D-CNN），能够有效地处理长期和短期时间序列信息，同时还能够捕捉序列中的季节性和周期性变化。LSTNet最初是由中国科学院计算技术研究所的Guokun Lai等人于2018年提出的。

LSTNet模型的核心思想是利用CNN对时间序列数据进行特征提取，然后将提取的特征输入到LSTM中进行序列建模。LSTNet还包括一个自适应权重学习机制，可以有效地平衡长期和短期时间序列信息的重要性。LSTNet模型的输入是一个形状为(T, d)的时间序列矩阵，其中T表示时间步数，d表示每个时间步的特征维数。LSTNet的输出是一个长度为H的预测向量，其中H表示预测的时间步数。在训练过程中，LSTNet采用均方误差（MSE）作为损失函数，并使用反向传播算法进行优化。

二、摘要

多变量时间序列预测是跨多个领域的重要机器学习问题，包括太阳能发电厂能量输出、电力消耗和交通拥堵情况的预测。在这些实际应用中出现的时间数据通常涉及长期和短期模式的混合，对于这些模式，自回归模型和高斯过程等传统方法可能会失败。在本文中，我们提出了一种新颖的深度学习框架，即长期和短期时间序列网络 (LSTNet)，以应对这一开放挑战。 LSTNet 使用卷积神经网络 (CNN) 和循环神经网络 (RNN) 来提取变量之间的短期局部依赖模式，并发现时间序列趋势的长期模式。此外，我们利用传统的自回归模型来解决神经网络模型的尺度不敏感问题。在我们对具有重复模式的复杂混合的现实世界数据的评估中，LSTNet 比几种最先进的基线方法实现了显着的性能改进。所有数据和实验代码均可在线获取。

三、研究背景

??多元时间序列预测是一个跨领域且重要的机器学习问题。在实际应用中的时态数据往往既具有长期模式也具有短期模式。传统的向量自回归模型无法捕捉多元信号的复杂非线性关系，从而以效率为代价导致性能下降；而高斯过程由于核矩阵的逆运算，在多元时间序列预测上也具有高计算复杂度。

四、创新点

?1、针对时态数据中的长短期模式，提出LSTNet模型，通过对多种模型的组合实现对混合、重复时序的分析与预测。

???2、针对间隔周期非常长的数据，通过改进GRU提出一种循环跳跃结构，对时序间的相关性进行了捕获。

五、问题分析

????????真实数据中，经常出现短期和长期模式混合的情景。下图绘制了高速公路每小时的占用率，以天为单位的周期可反映早晚之间的差异，以周为单位的周期可反映工作日和周末的差异。一个好的时间序列预测模型应该同时捕捉这两种重复出现的模式，从而进行准确的预测。

?已知时间序列Y=\left \{ y_{1},y_{2},...,y_{T} \right \}，其中y_{t}\in \mathbb{R}^{n}，n是变量的维数，本文的目标是以滚动预测的方式预测一系列未来信号。也就是说，假设Y=\left \{ y_{1},y_{2},...,y_{T} \right \}已知，预测目标则为y_{T+h}(h是当前时间向前预测的步长)。设时间t时的输入矩阵为X_{T}=\left \{ y_{1},y_{2},...,y_{t} \right \}\in \mathbb{R}^{n\times T}

六、模型框架

? ?

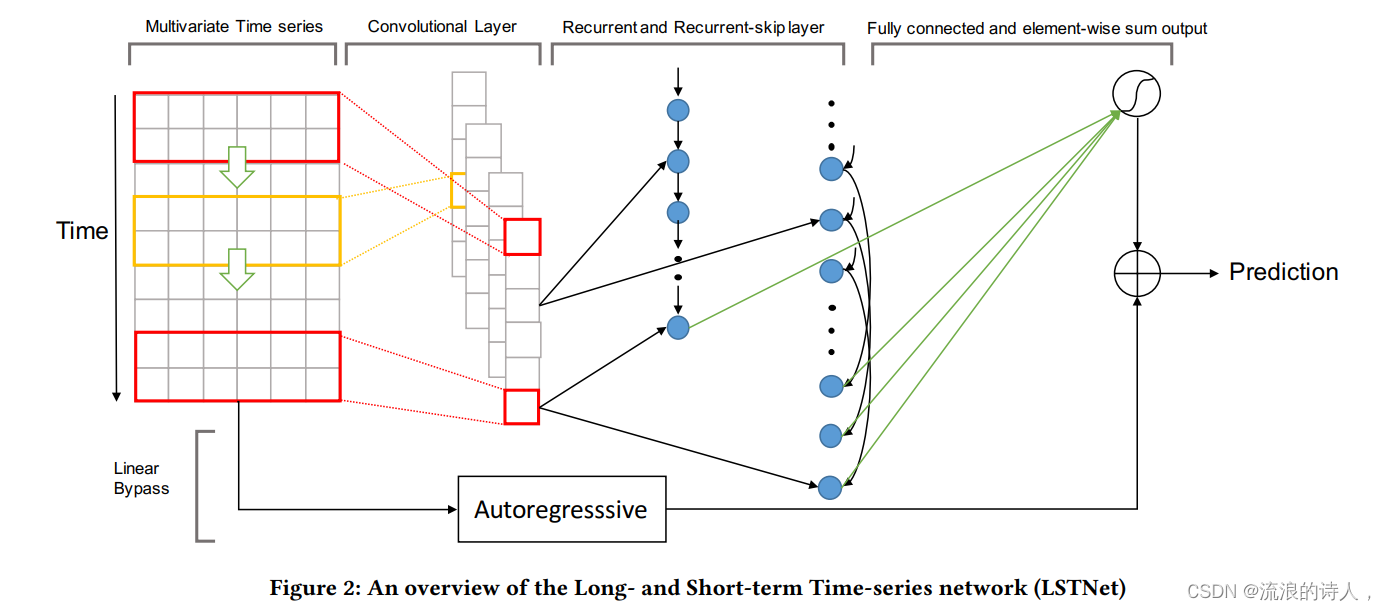
根据图示来看，整个流程即：

  • 输入至卷积层
  • 卷积输出至RNN
  • RNN做Skip操作
  • Skip至FCN 然后 + AR

它利用两个卷积层的优势来发现局部多维输入变量和循环层之间的依赖模式，以捕获复杂的长期依赖关系。一种新颖的循环结构，即 Recurrent-skip，旨在捕获非常长期的依赖模式，并使优化更容易，因为它利用了输入时间序列信号的周期性特性。最后，LSTNet 在非线性神经网络部分并行加入了传统的自回归线性模型，这使得非线性深度学习模型对于违反尺度变化的时间序列更加鲁棒。在真实世界季节性时间序列数据集的实验中，我们的模型始终优于传统的线性模型和 GRU 递归神经网络

?

1、卷积层

????????LSTNet的第一层是一个没有池化的卷积网络，旨在提取时间维度上的短期模式以及变量之间的局部依赖关系。卷积层由多个滤波器组成，滤波器的宽度为ω，高度为n(高度设置为与变量数量相同)。第k个滤波器扫过输入矩阵X并产生

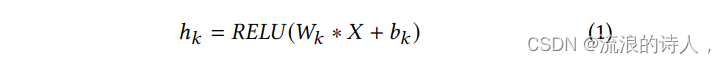
??通过在输入矩阵X的左侧填充零，使每个向量h_{k}的长度为T。卷积层的输出矩阵大小为dc×T，其中dc为滤波器个数。

2、循环层

????????卷积层的输出同时输入到循环层和循环跳跃层。循环层使用门控循环单元（GRU），用以捕获时间序列的时间依赖性以及长期模式。

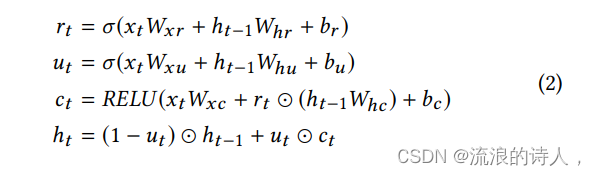
P是跳过的隐藏单元数量。

????????接下来，使用一个密集层组合循环层和循环-跳跃层的输出。密集层的输入包括时间t时循环层的隐藏状态，记作?h_{t}^{R}，以及从时间t-p+1至t时循环-跳跃层的p个隐藏状态，记作\small h_{t-p+1}^{S},h_{t-p+2}^{S},...,h_{t}^{S}；输出的计算公式为

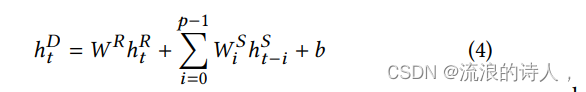
?hDt是时间t时神经网络的预测结果。

4、时间注意力层

????????循环-跳跃层需要一个预定义的超参数p，这对于非季节性的时间序列预测或周期长度随时间变化的预测是不利的。为缓解这一问题，引入注意力机制，它学习输入矩阵每个窗口位置的隐藏表示的加权组合。具体的，在当前时间t时的注意力权重可以按如下公式计算：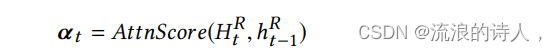

5、自回归层

????????神经网络模型的一个主要缺点是输出的尺度对输入的尺度不敏感。在特定的真实数据集中，输入信号的尺度会以非周期的方式不断变化，这就大大降低了神经网络模型的预测精度。

七、实验部分

1、数据集准备

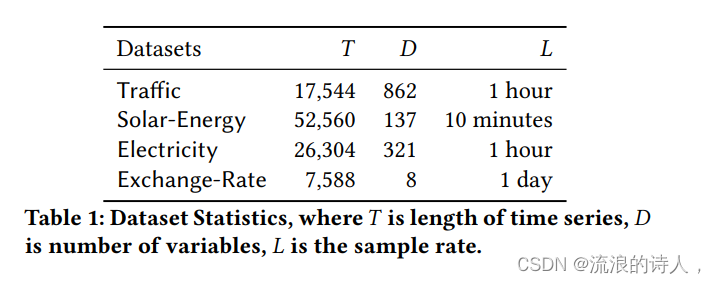
????????使用四个公开可用的基准数据集，分别为Traffic、Solar-Energy、Electricity、Exchange-Rate。所有数据集按时间顺序分为训练集(60%)、验证集(20%)和测试集(20%)

为了检验时间序列数据中是否存在长期和/或短期重复模式，对四个数据集中随机选择的一些变量绘制了自相关图。

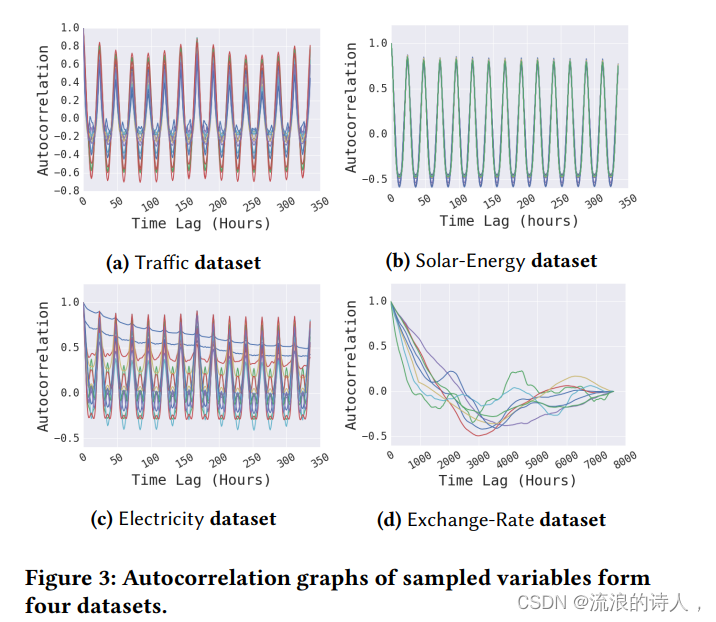
在 (a)，(b)和(c)图中看到，在Traffic, Solar-Energy和Electricity数据集中有高自相关性的重复模式，但在exchange rate数据集中没有。在Traffic与Electricity数据集的曲线图中，可以观察到短期的 (每24小时)和长期的 (每7天)的重复模式；在图(d)中，几乎看不到任何重复的长期模式。

2、评价指标

相对平方误差(RSE)、经验相关系数(CORR)，其中RSE值越小越好，CORR值越大越好。

3、实验结果

?

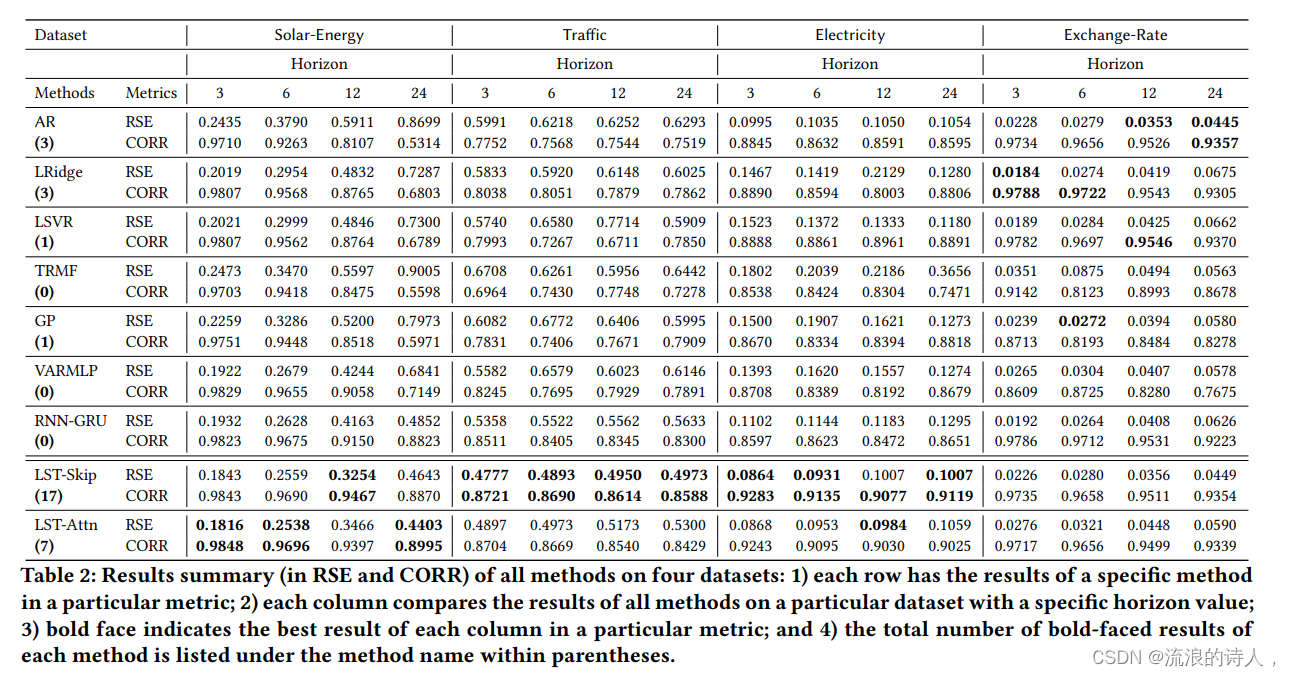
4、消融实验
? ? ? ?

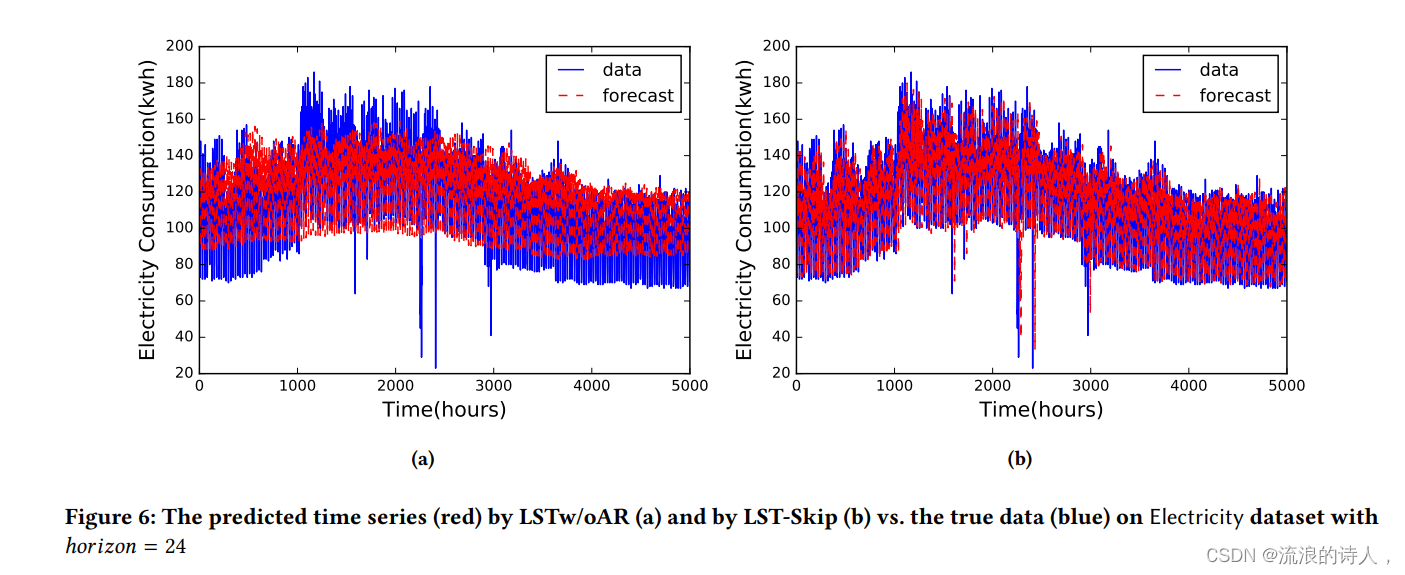
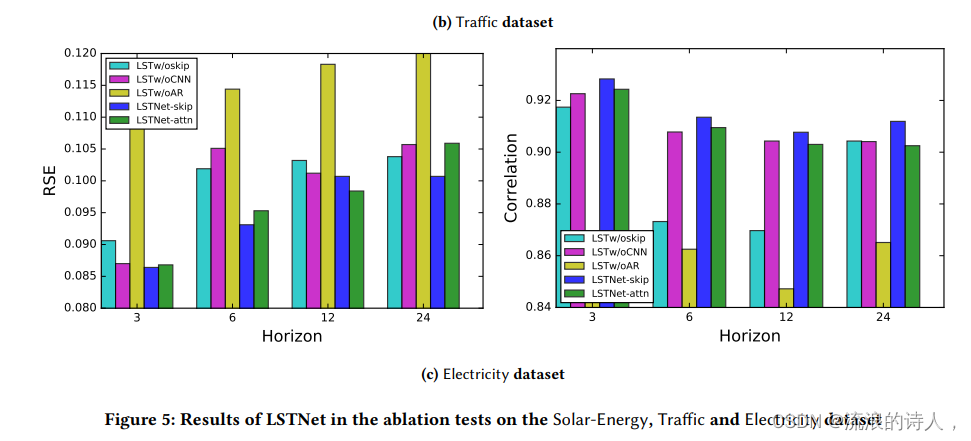
? ? ?为证明模型的效率，本文进行了消融研究。具体来说，就是在LSTNet框架中每次删除一部分。模型命名如下：为了说明LSTNet在对时间序列数据中短期和长期重复模式混合建模方面的成功，本文还比较了LSTNet和VAR在Traffic数据集中特定时间序列上的性能。

? ? ? ? LSTw/oskip：在LSTNet模型上删除循环-跳跃层和注意力层。

? ? ? ? LSTw/oCNN：在LST-skip模型上删除卷积层。

? ? ? ? LSTw/oAR：在LST-skip模型上删除自回归层。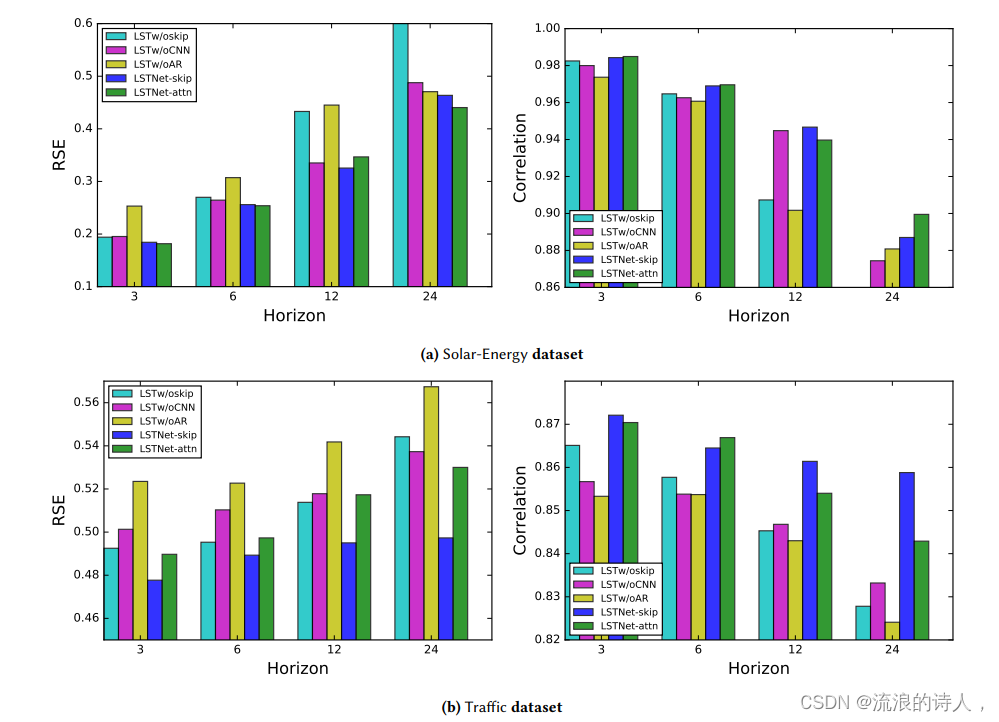

?

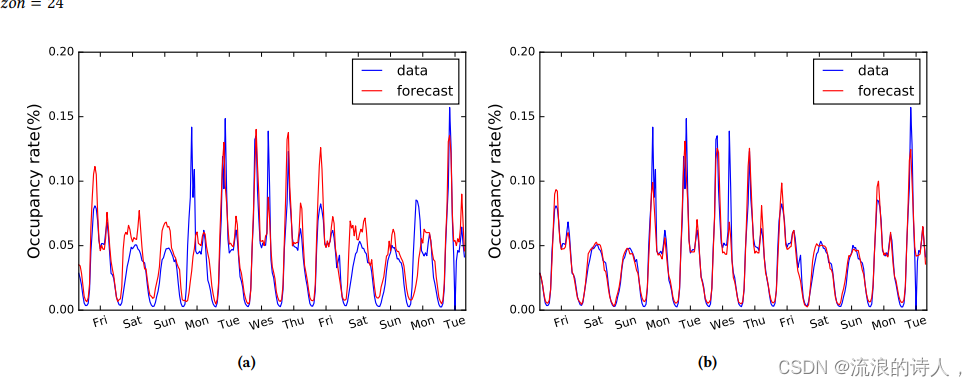
5、长/短期混合模式的研究

????????为了说明LSTNet在对时间序列数据中短期和长期重复模式混合建模方面的成功，本文还比较了LSTNet和VAR在Traffic数据集中特定时间序列上的性能。

八、总结

? ?本文提出了一种新的深度学习框架(LSTNet)用于多变量时间序列预测。通过结合卷积、循环神经网络以及自回归层的优势，显著改善了多个基准数据集上的时间序列预测的结果；通过深入分析和经验验证，LSTNet模型成功捕捉了数据中的短期和长期重复模式，并结合线性和非线性模型进行了稳健的预测。
?

文章来源:https://blog.csdn.net/qq_59482564/article/details/135223681
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章