格密码基础：光滑参数

目录

一. 铺垫高斯函数

二. 光滑参数图形理解

三. 光滑参数与格基本区

3.1 高斯与均匀分布的统计距离

3.2 光滑参数理解

四. 光滑参数与最短向量

五. 光滑参数与连续最小值

六. 光滑参数与对偶格的上界

七. 光滑参数与格的上界

八. 小结

---

一. 铺垫高斯函数

定义高斯密度函数如下：

进一步形成新的高斯密度函数：

注意此处的函数输入为N维，也就是。根据高斯函数对长度的限制，可得：

二. 光滑参数图形理解

首先，我们均匀选择一些格点，以二维为例子，这些格点处对应的概率大致相等。接着，我们把每个格点外加一个高斯噪声，可得：

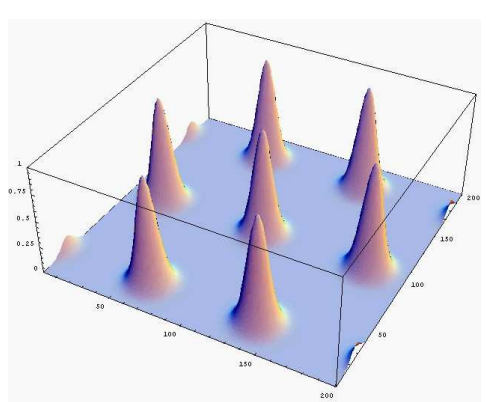
当我们增大高斯噪声的方差，图形会变成：

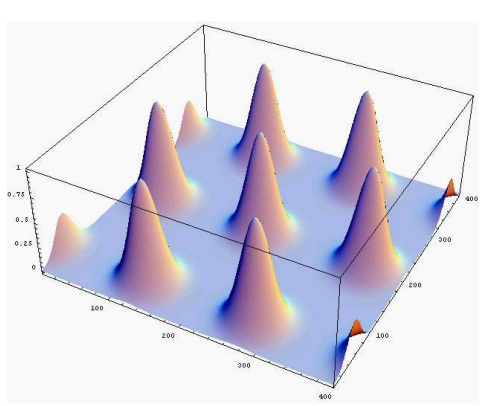
如果继续增大高斯噪声会出现：

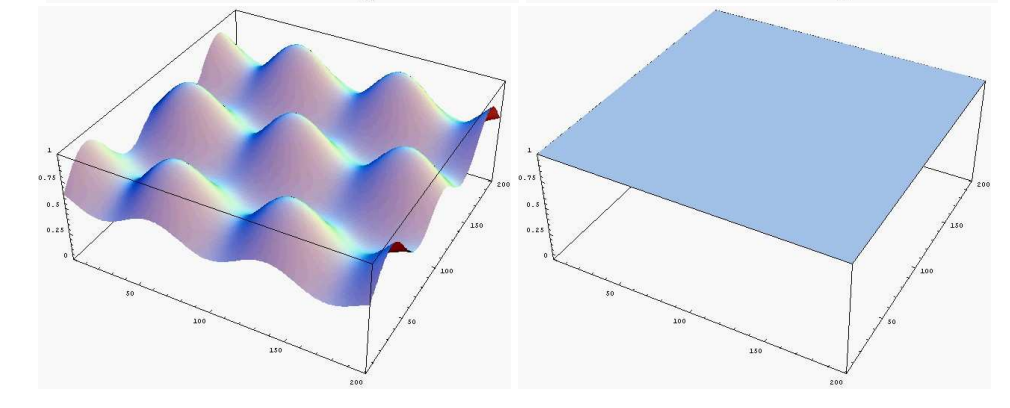
很明显当s越来越大后，图形会越来越接近均匀分布。在网络安全中，均匀分布非常重要，格的光滑参数就是研究当s取多大时，此均匀分布会出现。

三. 光滑参数与格基本区

3.1 高斯与均匀分布的统计距离

格的格基记为B，格基本区写做P(B)，基本区上的均匀分布为：

对偶格的行列式与格的行列式互为倒数，所以可得：

高斯函数记为，将高斯函数中的每个点都 模基本区（mod P(B)），可以得到新的函数分布：

第一个等号：Y(x)分布的意义，与x在模基本区下相等；

第二个等号：与之间的关系，另外基本区内的点加上所有的格点，可以遍历整个扩展空间内的点；

利用泊松求和公式以及傅里叶变换的性质，对分布Y(x)进一步运算可得：

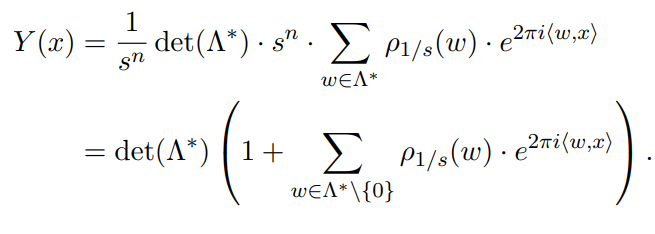
如果有人感兴趣这一步的证明，欢迎留言，以后可以补上。

现在我们来计算新得到的分布Y(x)与均匀分布U(x)之间的统计距离，如下：

取该距离的上限，基本区的体积记为格行列式的值，再带入Y(x)的表达式，可得：

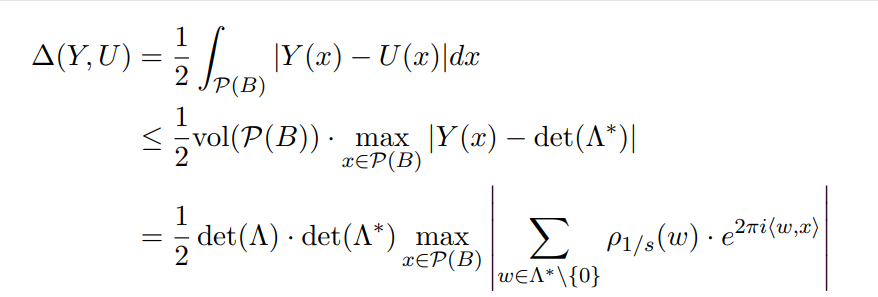
指数的取值不会超过1，对偶格的行列式与格的行列式互为倒数，进一步化简可得：

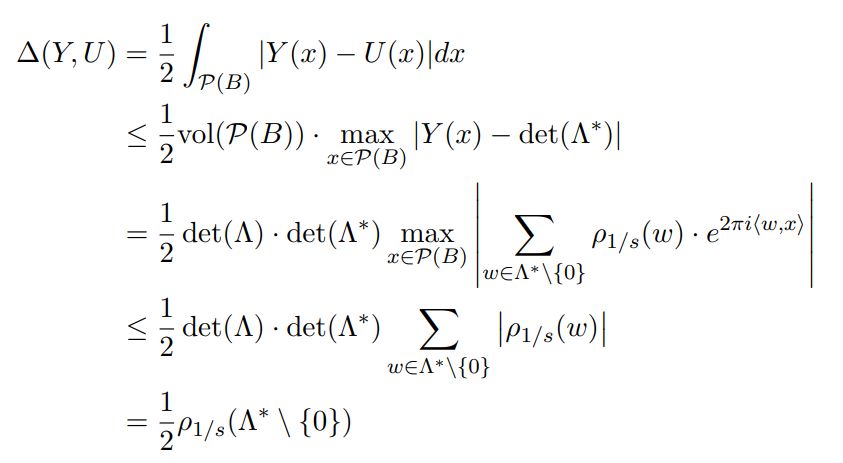
将以上，总结为形式化的定义可得：

3.2 光滑参数理解

以上讨论告诉我们：

最小的s，使其满足：

对应的s就被称之为格的光滑参数，记作

很明显，当s越来越小时，越来越大，也就是：

当s越来越大时，越来越小，也就是：

所以可以把看成关于s的函数，并且该函数为连续型且严格单调递减的函数。

以下理解非常重要。

也就是说，当高斯函数的标准差s大于光滑参数时，也就是：

可得高斯函数与均匀分布之间的距离最多为（注意两个分布均定义在基本区P(B)上）。光滑参数是连接高斯分布与均匀分布很好的桥梁。

四. 光滑参数与最短向量

当时，可得光滑参数的下界：

证明：

令高斯分布的参数s等于对偶格最短向量的倒数，于是：

令y代表对偶格的最短向量，也就是：

带入运算可得：

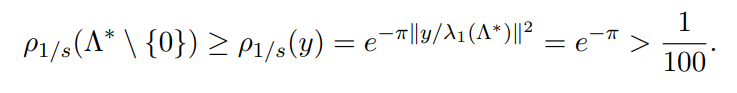
证明完毕。

五. 光滑参数与连续最小值

结合转移定理（Banaszczyk transference theorem），以上定理可得：

当时，可得光滑参数的下界：

六. 光滑参数与对偶格的上界

当，可得光滑参数的上界：

证明：

令高斯分布的参数s等于：

带入高斯分布中运算可得：

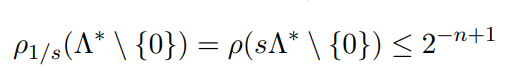
第一个等号：高斯函数的性质；

第二个不等号：对偶格的性质

所以可得：

证明完毕。

七. 光滑参数与格的上界

当，可得光滑参数的上界：

利用转移定理结合上一个性质即可证明。

其实这个界还不够紧致，实际上，当时，光滑参数的上界为：

八. 小结

格理论的研究起源于 17-19 世纪， 数学家 Kepler 和 Gaussian 研究在低维空间中堆放等半径的小球，当所有球的球心构成一个格时，计算得出了堆积球密度的最大值。 在19 世纪中叶，Minkowski 和 Hermit 等数学家逐渐发展了格堆积理论和格覆盖理论。 计算球的最大格堆积密度相当于在格点中求解最短向量问题（Shortest Vector Problem， SVP） ， 计算球的最小覆盖密度相当于在格点中求解最近格点问题（Closest Vector Problem， CVP）， 两者都是格密码的核心数学难题。

1998 年， Ajtai 证明了SVP在范数下，当近似因子小于时是 NP-Hard 的， 即不存在多项式时间的算法可以求解近似版本 SVP（Approximate Shortest Vector Problem，?）。在保证SVP在和范数下是NP-hard的同时，计算出近似因子的上界为和。2003年，Dinur等计算出当近似因子为时，近似版本 CVP（Approximate Closest Vector Problem）是 NP-hard 的。
算法复杂性理论研究基于求解问题所要花费的时间、 空间资源（比特数、 带数、 逻辑门数） 等。 通过考察求解某个问题的不同算法复杂程度来衡量问题的难易程度． 由此将问题划分为不同的类型：

经典复杂性分类	定义
P	确定型 单带图灵机在多项式时间内可判定的语言类
NP	某个非确定型多项式时间图灵机判定的语言类
NPC	NP 问题子集， 可以通过多项式时间算法归约到一个 NP 问题上

格上困难问题是计算复杂性理论的重要研究内容， 基于格的密码方案的可证明安全性依赖格上问题的难解度， 格上许多困难问题在目前已被证明是NP难的， 其中包括最短线性无关向量问题（SIVP） ， 短整数解问题（SIS） 。 SIVP 问题和 SIS 问题都可以归约到格上最差情况的困难问题， 所以有些格密码方案是基于上述困难问题设定，其在标准模型下该网络安全方案是具有抗量子的特效。