从零学算法5

5.给你一个字符串 s，找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。
示例 1：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。
示例 2：
输入：s = “cbbd”
输出：“bb”

• 暴力解法。无非就是双重循环，截取出所有子串，判断是否为回文串，然后取最大值。稍微优化一下，如果此时子串长度小于当前最长的回文子串 max 就直接跳过，当前子串长度为 j - i +1

•   String s;
    public String longestPalindrome(String s) {
        this.s = s;
        int n = s.length();
        // start：最长回文子串起始下标
        int max = 0,start = 0;
        for(int i=0;i<n;i++){
            for(int j=i;j<n;j++){
                if(j-i+1 < max)continue;
                if(isPalindrome(i,j)){
                    max = Math.max(max, j-i+1);
                    start = i;
                }
            }
        }
        return s.substring(start, start+max);
    }
    public boolean isPalindrome(int i,int j){
    // 根据回文串对称的性质从左右两端往中间找，有不一样的就不是
        while(i<j){
            if(s.charAt(i++)!=s.charAt(j--))return false;
        }
        return true;
    }
  

• 中心扩散法。遍历 s 的每个下标，以其为中心点向两边扩散，看是否为相同字符，就能得到以该点为中心的回文串。但是回文串不一定为奇数长度，即中心点处长度不一定为 1，比如 abccba，中心点处其实为 cc，所以就在扩散时定义初始左右起点为这两个字符的下标即可。

•   public String longestPalindrome(String s) {
        int n = s.length();
        int max = 0,start = 0;
        for(int mid=0;mid<n;mid++){
            if(n-mid<max/2)break;
            int i=mid,j=mid;
            //有相同的点就移动初始右端点
            // 为什么不需要移动左端点?看下面 mid = j 部分
            while(j<n-1 && s.charAt(j)==s.charAt(j+1))j++;
            // i~j 这一段的点作为中心处已经在这一轮考虑过，所以之后直接跳过即可
            // 同时这也保证了下一轮 i 初始化为 mid 时,i 的左边不会和 i 处字符重复
            // 相当于在上一轮就移动了左端点，遍历顺序为从左到右，所以首轮左处无端点无需处理
            mid = j;
            // 向两端延伸求最大回文串长度
            while(i>0 && j<n-1 && s.charAt(i-1)==s.charAt(j+1)){
                i--;
                j++;
            }
    		// 更新最大值和最大回文子串起始下标
            if(j-i+1>max){
                max = j-i+1;
                start=i;
            }
        }
        return s.substring(start, start+max);
    }
  

• 动态规划法。根据上面中心扩散法判断回文串的方式，可以大致看到动态规划的雏形。假定 boolean dp[left][right] 表示子串 s[left:right] 是否为回文串。那么从 dp[left][right] 为 true 开始，如果 s.charAt(left-1)==s.charAt(right+1)，就可以得到 dp[left-1][right+1] 为 true，即 dp[l][r] = dp[l+1][r-1] && s.charAt(l-1)==s.charAt(r+1)。得到递推公式以后还需要确定一下边界条件。以下 s.charAt(left) 我就简写成 s[left] 了，如果 s[left]!=s[right]，说明当前子串左右两端字符不相同，那么你怎么都不会是回文串；如果相同，那么当子串长度小于等于 3 时，你一定是回文串，比如 aba,bb,a，否则就根据 dp[left + 1][right - 1] 递推。
• 考虑到dp[left][right] 依赖 dp[left + 1][right - 1] 的特性，比如 dp[0][3]，要先知道 dp[1][2] ，那 left 在外层遍历是肯定不可能先得到 dp[1][x] 再得到 dp[0][x] 的，所以遍历顺序需要调整为外层为 right，内层为 left

•   public String longestPalindrome(String s) {
        int n = s.length();
        boolean[][] dp = new boolean[n][n];
        int max = 0,start = 0;
        for(int j=0;j<n;j++){
            for(int i=0;i<=j;i++){
                if(s.charAt(i)!=s.charAt(j))continue;
                if(j-i<3)dp[i][j]=true;
                else dp[i][j]=dp[i+1][j-1];
                if(dp[i][j] && j-i+1>max){
                    max = j-i+1;
                    start=i;
                }
            }
        }
        return s.substring(start, start+max);
    }
  

• 长度为 1 的子串肯定是回文串，所以还可以根据这点稍微优化一下

•   int max = 1,start = 0;
    for(int j=1;j<n;j++){
        for(int i=0;i<j;i++){
  

• 马拉车算法（Manacher）：回文串有奇数 aba 和偶数 abba 两种形式，使用马拉车算法，会在字符串的每两个字符间以及字符首尾加上一个特殊字符，这样最终字符串长度都会为奇数，同时，原本的每个回文串的长度也会都变成奇数，以上面两个字符串为例就可以证明
• aba->*a*b*a*
• abba->*a*b*b*a*
• 其实就是奇数加偶数必定为奇数
• 再引用一个变量回文半径，表示回文串左边或右边到中心点的长度，比如 *a*b*a* 回文半径为 *a*b 或者 b*a* 的长度也就是 4， *a*b*b*a* 回文半径为 5
• 铺垫完毕，进入正题，中心扩散法每次换一个中心点，都要重新计算此时以 i 点为中心点的回文串长度，而马拉车在中心扩散法的基础上改进，可以利用之前的结果。
• 因为遍历顺序是从左到右，所以我们取之前的回文串结果中右边界最大的一个，利用它推出当前以 i 为中心的回文串长度。我们就假设之前的那个结果中心点为 maxCenter，左右端点为 left 和 maxRight。我们根据 i 的位置划分出不同情况下怎么推出当前结果

  1. i < maxRight，那么以 maxCenter 为对称中心对称过去的点 j 肯定在 left 到 maxCenter，如果以 j 为中心点得到的回文串也在 left 到 maxCenter 之内，那根据对称的性质，i 对应的结果和 j 对应的一样，下图顺便说明了得到 j 点的计算公式，把 left 带入 0 为例子比较容易推导， p[] 为回文串半径数组
     

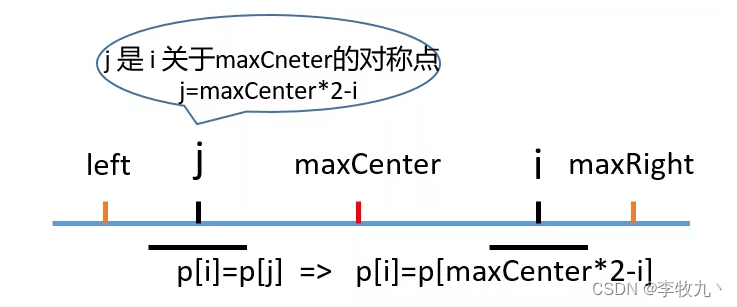
  2. i < maxRight，但是以 j 为中心的回文串长度超过了 left，还是根据对称，我起码可以肯定我的回文串半径最小也等于 j - left ，也就是 maxRight - i，我们以此为基础用中心扩散法继续扩散即可
     

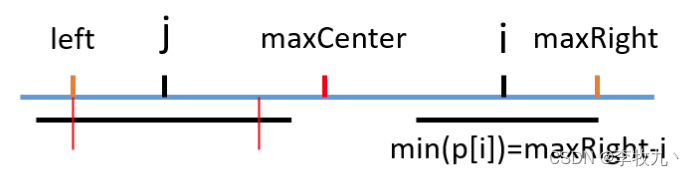
  3. i > maxRight，那没办法了，老老实实从头开始中心扩散法吧

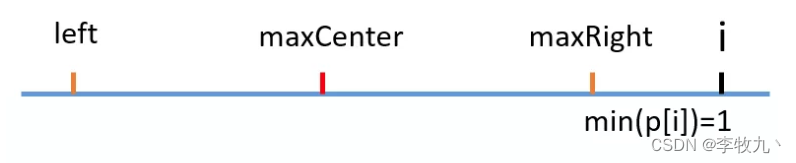
• i 为什么没有小于 maxCenter 的情况，因为 maxCenter 就是我们之前不断遍历得到的某个 i，新的 i 当然大于之前的 i 了

•   int charLen = s.length();//源字符串的长度
    int length = charLen * 2 + 1;//添加特殊字符之后的长度
    char[] chars = s.toCharArray();//源字符串的字符数组
    char[] res = new char[length];//添加特殊字符的字符数组
    int index = 0;
    //添加特殊字符
    for (int i = 0; i < res.length; i++) {
        res[i] = (i % 2) == 0 ? '#' : chars[index++];
    }
  
    //新建p数组 ，p[i]表示以res[i]为中心的回文串半径
    int[] p = new int[length];
    //maxRight(某个回文串延伸到的最右边下标)
    //maxCenter(maxRight所属回文串中心下标),
    //resCenter（记录遍历过的最大回文串中心下标）
    //resLen（记录遍历过的最大回文半径）
    int maxRight = 0, maxCenter = 0, resCenter = 0, resLen = 0;
    //遍历字符数组res
    for (int i = 0; i < length; i++) {
        if (i < maxRight) {
            //情况一，i没有超出范围[left,maxRight]
            //2 * maxCenter - i其实就是j的位置，实际上是判断p[j]<maxRight - i
            // maxRight - i 其实就是 j-left，也就是说 j 的回文半径在 left ~ j
            if (p[2 * maxCenter - i] < maxRight - i) {
                //j的回文半径没有超出范围[left,maxRight]，直接让p[i]=p[j]即可
                p[i] = p[2 * maxCenter - i];
            } else {
                //情况二，j的回文半径已经超出了范围[left,maxRight]，我们可以确定p[i]的最小值
                //是maxRight - i，至于到底有多大，后面还需要在计算
                // i - p[i] 表示以 i 为中心， p[i] 为半径的回文串的左端点，同理 i + p[i] 为右端点
                // 半径不断增加就等于中心点不断向外扩散
                p[i] = maxRight - i;
                while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
                    p[i]++;
            }
        } else {
            //情况三，i超出了范围[left,maxRight]，就没法利用之前的已知数据，而是要一个个判断了
            p[i] = 1;
            while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
                p[i]++;
        }
        // 匹配完之后，如果右边界i + p[i]超过maxRight，那么就更新maxRight和maxCenter
        // 因为主要看 i 相对右边界来推导结果，所以能更新右边界就更新
        if (i + p[i] > maxRight) {
            maxRight = i + p[i];
            maxCenter = i;
        }
        //记录最长回文串的半径和中心位置
        if (p[i] > resLen) {
            resLen = p[i];
            resCenter = i;
        }
    }
    //计算最长回文串的长度和开始的位置
    resLen = resLen - 1;
    int start = (resCenter - resLen) >> 1;
    //截取最长回文子串
    return s.substring(start, start + resLen);
  

• 如下图所示，有特殊字符的回文半径 - 1 其实就是原始回文串的长度，这也就是 resLen = resLen - 1; 的由来
  
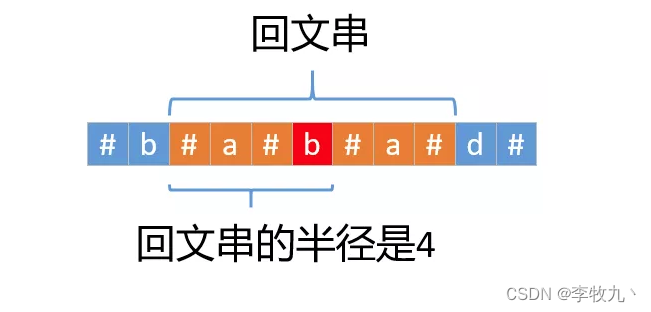
• 上面三种情况还能合并，把他们都看成确定半径以及扩散这两步即可，情况 1 确定完半径以后不满足扩散条件所以不会扩散，情况 2 和 3 也就是初始半径不同，都会扩散

•  int charLen = s.length();//源字符串的长度
   int length = charLen * 2 + 1;//添加特殊字符之后的长度
   char[] chars = s.toCharArray();//源字符串的字符数组
   char[] res = new char[length];//添加特殊字符的字符数组
   int index = 0;
   //添加特殊字符
   for (int i = 0; i < res.length; i++) {
       res[i] = (i % 2) == 0 ? '#' : chars[index++];
   }
  
   //新建p数组 ，p[i]表示以res[i]为中心的回文串半径
   int[] p = new int[length];
   //maxRight(某个回文串延伸到的最右边下标)
   //maxCenter(maxRight所属回文串中心下标),
   //resCenter（记录遍历过的最大回文串中心下标）
   //resLen（记录遍历过的最大回文半径）
   int maxRight = 0, maxCenter = 0, resCenter = 0, resLen = 0;
   //遍历字符数组res
   for (int i = 0; i < length; i++) {
       //合并后的代码
       p[i] = maxRight > i ? Math.min(maxRight - i, p[2 * maxCenter - i]) : 1;
       //上面的语句只能确定i~maxRight的回文情况，至于maxRight之后的部分是否对称，
       //就看是否需要一个个去匹配了，匹配的时候首先数组不能越界
       while (i - p[i] >= 0 && i + p[i] < length && res[i - p[i]] == res[i + p[i]])
           p[i]++;
       //匹配完之后，如果右边界i + p[i]超过maxRight，那么就更新maxRight和maxCenter
       if (i + p[i] > maxRight) {
           maxRight = i + p[i];
           maxCenter = i;
       }
       //记录最长回文串的半径和中心位置
       if (p[i] > resLen) {
           resLen = p[i];
           resCenter = i;
       }
   }
   //计算最长回文串的长度和开始的位置
   resLen = resLen - 1;
   int start = (resCenter - resLen) >> 1;
   //截取最长回文子串
   return s.substring(start, start + resLen);