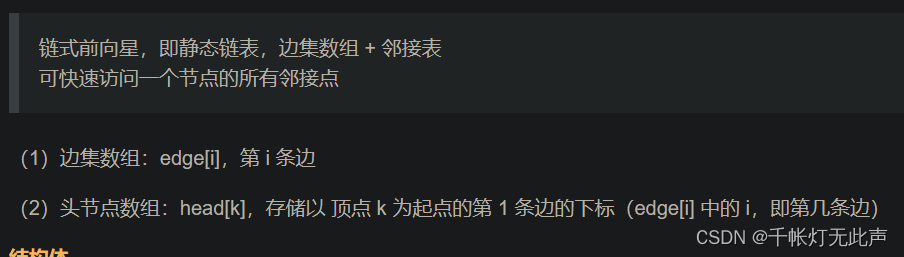
最短路径(Dijstra, Floyd, Bellman-Ford, SPFA)
个人认为,新学的算法模板,最好敲上两三遍,再开始做题,前 2 遍可以跟着敲,第 3 遍,有时间,就理解着默写一遍
目录
🌼前言
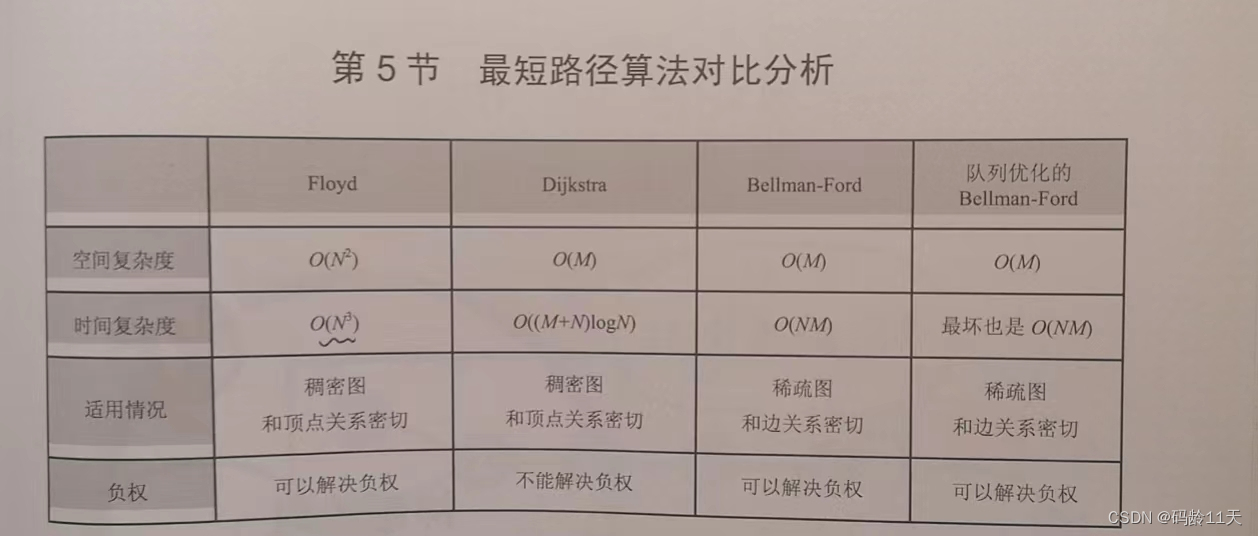
Floyd算法
时间复杂度高,但实现容易(5行核心代码),可解决负权边,适用于数据范围小的
Dijkstra算法
不能解决负权边,但具有良好扩展性,且复杂度较低
Bellman-Ford / 队列优化Bellman-Ford
可解决负权边,且复杂度较低
🍉Dijstra && Floyd 详解
Dijstra 和 Floyd 算法,就不重新写了
🍈Bellman - Ford && SPFA 详解
Bellman
Bellman 可以解决 负权边,Dijstra 由于使用贪心,无法解决负权边
它和 Dijstra 类似,都通过 松弛 找到 最短路
Dijstra,贪心选取未被处理的,具有最小权值的点,然后从确定点出边进行松弛
Bellman,对所有边进行松弛,共 n - 1 次(如果第 n 次仍可以松弛,则一定存在 负环)
步骤
(1)数据结构:需要对边松弛,采用 边集数组 存储,每条边三个域:
起点 a,终点 b,边权 w
(2)松弛操作:对每条边 j(a, b, w)
if (dis[e[j].b] > dis[e[j].a] + e[j].w) dis[e[j].b] = dis[e[j].a] + e[j].w;dis[v] 表示源点 1 到 点 v 的最短长度
e[j].w? --? e[j].a 到 e[j].b 的距离(e[j] 这条边的起点到终点)
dis[e[j].b]? --? 1 ~ e[j].b 的距离
dis[e[j].a]? --? 1 ~ e[j].a 的距离
(3)重复松弛:?n - 1 次
(4)负环判定:再执行 1 次,即第 n 次松弛,如果仍然可以松弛,存在负环,return true
Bellman 代码
虽然不是很理解,为什么书里,dis 要初始化为 0x3f,即 十进制 的 63?
// 源点 u 到 其他点 的最短长度,并判断负环
bool bellman_ford(int u)
{
memset(dis, 0x3f, sizeof(dis));
dis[u] = 0;
for (int i = 1; i < n; ++i) { // 对所有边进行 n - 1 次松弛
bool flag = 0;
for (int j = 0; j < m; ++j) // m 条边
if (dis[e[j].b] > dis[e[j].a] + e[j].w) {
dis[e[j].b] = dis[e[j].a] + e[j].w; // 松弛
flag = true;
}
// 一点优化,提前结束 n - 1 次松弛
if (flag == false) return false; // 所有边松弛完了,没有负环
}
// 执行第 n 次松弛
for (int j = 0; j < m; ++j)
if (dis[e[j].b] > dis[e[j].a] + e[j].w)
return true; // 有负环
return false;
}队列优化
松弛操作必定只会发生在,最短路径松驰过的前驱节点
(前驱节点 即 松弛过的节点)
用一个队列记录松弛过的节点,可以避免冗余运算
(因为 Bellman 每次松弛,都要对所有边操作一次,但是有些边已经更新过了,就会重复松弛)
(为了避免重复操作,已松弛的点加入队列,未松弛的点不加入队列)
这就是 队列优化的 Bellman-Ford,即 SPFA 算法
(避免对已更新的节点,重复松弛)
SPFA
Shortest Path Faster Algorithm,SPFA,是 Bellman 的队列优化版本
用于求解,含负权边的单源最短路? &&? 判负环
最坏情况,SPFA 时间复杂度? ==? Bellman,O(nm)
但是稀疏图,效率较高,为 O(km),k 为较小常数
步骤
(1)创建队列:源点 u 入队,标记 u 在队列,u 入队次数 +1
(2)松弛操作:取队头节点 x,标记 x 不在队列
for() 遍历 x 所有出边 i(x, v, w)? ? ? ? ?--? ? ? 起点 x 到 终点 v 的边是 e[i]
如果 dis[v] > dis[x] + e[i].w,则松弛? --? dis[v] = dis[x] + e[i].w
如果 节点 v 不在队列,判断 v 的入队次数 + 1,如果 >= n,说明有 负环, return true
否则 v 入队,标记在队列
👆 入队次数 >= n,说明有负环,这点不是很理解,先记 模板 吧
(3)重复松弛:直到队列为空
SPFA? 代码
// 源点 u 到 其他点的最短长度 && 判负环
bool spfa(int u)
{
queue<int> q;
memset(vis, 0, sizeof(vis)); // 标记在队列里
memset(sum, 0, sizeof(sum)); // 统计入队次数
memset(dis, 0x3f, sizeof(dis));
vis[u] = 1; // 源点 u 入队
dis[u] = 0;
sum[u]++;
q.push(u);
while (!q.empty()) {
int x = q.front(); // 取队头
q.pop();
vis[x] = 0; // 取消标记
// 链式前向星存图
// 遍历 x 所有邻接边
// ~i 等价于 i != -1
for (int i = head[x]; ~i; i = e[i].next) {
int v = e[i].to; // x 点邻接点
// 点 x 到 点 v 的距离 e[i].w
if (dis[v] > dis[x] + e[i].w) {
dis[v] = dis[x] + e[i].w;
if (!vis[v]) { // v 不在队列
if (++sum[v] >= n) return true;
vis[v] = 1; // v 入队
q.push(v);
}
}
}
}
return false; // 队列为空,没有负环
}🌼刷题
👊重型运输 -- Dijstra
1797 -- Heavy Transportation (poj.org)
本题考察点有 3 个
(1)n 个顶点,m 条边,n <= 1000,m 没有给出,采用 链式前向星 OR 邻接矩阵 存图
(2)边数可能较多,采用 scanf() 读入,而不用 cin,否则 Time Limited Exceeded
对比?
1)邻接表是用链表实现的,可以动态的 增加 / 删除 边
2)链式前向星是用结构体数组实现的,是静态的,需要一开始知道数据范围,开好数组大小。
相比之下,邻接表灵活,链式前向星好写
3)邻接矩阵呢,更适用于,不需要更新 / 删除的稠密图(边多,点少)
4)链式前向星 = 静态链表,邻接表 = 动态链表
(3)难点:
理解题目,并转化为 Dijstra👇
// 找确定点 for (j = 2; j <= n; ++j) { // 顶点 2 开始 if (!book[j] && dis[j] > Max) { Max = dis[j]; u = j; } } book[u] = 1; // 顶点 1 到 u 已确定最小承重 dis[u] // 从被确定点出边, 更新每一个点的最小承重 for (v = 2; v <= n; ++v) {// 顶点 2 开始 dis[v] = max(dis[v], min(dis[u], e[u][v])); // 先找到每一条路的最小承重 dis[u] // 作为确定值 // 1 ~ u 每一条路的最小承重找到了, 就是 dis[u] // 然后从 u 出发, 找 u 到其他点, 是否存在更小的 // 如果找到了 e[u][v] 更小 // 即 1 ~ v 的最小承重 可以更新 // min(dis[u], e[u][v]),1 ~ v 某一条路的最小承重 // 又因为,要取所有路径,的最大值 }可以对比下常规 dijstra👇
最短路之Dijkstra(15张图解)_dijkstra算法过程图解-CSDN博客
最关键的一行👇
dis[v] = max(dis[v], min(dis[u], e[u][v]));不要照搬 dijstra() 单源最短路的代码,因为这里是 最大的最小负重(权值)
(4)多组样例,每组都要初始化
(5)测试样例间,有空行,每次输出完答案要换行 2 次???
回顾 链式前向星
AC?-- 邻接矩阵
#include<iostream>
#include<cstdio> // scanf()
#include<cstring> // memset()
using namespace std;
int T, n, m, u, v, t1, t2, t3, i, j, cnt; // cnt 样例计数
int book[1010], e[1010][1010], dis[1010];
void dijstra()
{
// 初始化 dis[],最大的最小负重,的确定值
for (i = 1; i <= n; ++i)
dis[i] = e[1][i];
for (int i = 1; i < n; ++i) { // n - 1 次遍历
int Max = 0;
// 找确定点
for (j = 2; j <= n; ++j) { // 顶点 2 开始
if (!book[j] && dis[j] > Max) {
Max = dis[j];
u = j;
}
}
book[u] = 1; // 顶点 1 到 u 已确定最小承重 dis[u]
// 从被确定点出边, 更新每一个点的最小承重
for (v = 2; v <= n; ++v) {// 顶点 2 开始
dis[v] = max(dis[v], min(dis[u], e[u][v]));
// 先找到每一条路的最小承重 dis[u]
// 作为确定值
// 1 ~ u 每一条路的最小承重找到了, 就是 dis[u]
// 然后从 u 出发, 找 u 到其他点, 是否存在更小的
// 如果找到了 e[u][v] 更小
// 说明 1 ~ u ~ v 的最小承重可以更新
// 即 1 ~ v 的最小承重 可以更新
// min(dis[u], e[u][v]),1 ~ v 某一条路的最小承重
// 又因为,要取所有路径,的最大值
}
}
}
int main()
{
scanf("%d", &T);
while (T--) {
// 初始化 e[][], book[]
memset(e, 0, sizeof(e));
memset(book, 0, sizeof(book));
scanf("%d%d", &n, &m); // n 顶点, m 条边
// 读入边
while (m--) {
scanf("%d%d%d", &t1, &t2, &t3);
e[t1][t2] = t3;
e[t2][t1] = t3; // 无向边
}
dijstra();
printf("Scenario #%d:\n", ++cnt);
printf("%d\n\n", dis[n]); // 两次换行
}
return 0;
}AC?-- 链式前向星
多了个 struct {}e[maxe];? 和? add()
还有遍历邻接点的 for()
但是,因为 链式前向星,不是那么容易表示出 e[u][v] 这个负重,需要用 priority_queue 代替
具体过程我不是很理解,这里贴一下书里的 AC? 代码 和 GPT 的注释
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio> //scanf()
using namespace std;
const int maxn=1005,maxe=1000001;
const int inf=0x3f3f3f3f;
int T,n,m,w,cnt; // 定义变量 T, n, m, w, cnt
int head[maxn],dis[maxn]; // 定义数组 head 和 dis
bool vis[maxn];//标记是否已访问
struct node{
int to,next,w;
}e[maxe]; // 定义结构体 node 和数组 e
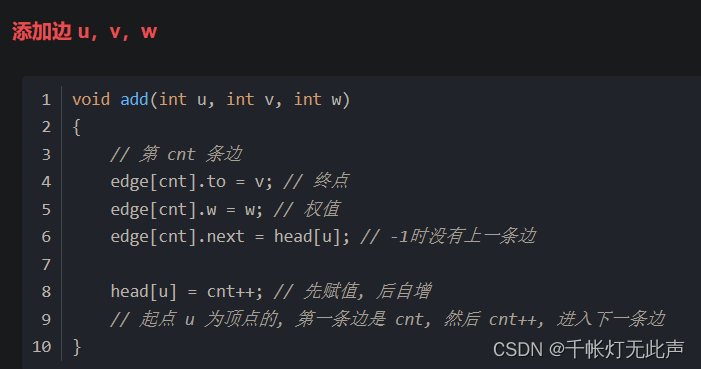
void add(int u,int v,int w){
e[cnt].to=v;
e[cnt].next=head[u];
e[cnt].w=w;
head[u]=cnt++; // 添加边函数,将边信息存入数组 e 和 head
}
void solve(int u){//dijkstra算法变形,求最小值最大的路径
priority_queue<pair<int,int> >q; // 创建一个优先队列 q,存储点的距离和编号
memset(vis,0,sizeof(vis)); // 初始化 vis 数组为 false
memset(dis,0,sizeof(dis)); // 初始化 dis 数组为 0
dis[u]=inf; // 起点距离为无穷大
q.push(make_pair(dis[u],u)); // 将起点压入队列
while(!q.empty()){
int x=q.top().second; // 取出队列中距离最大的点的编号
q.pop(); // 弹出队列中的元素
if(vis[x])
continue; // 如果该点已访问过,跳过当前循环
vis[x]=1; // 将该点标记为已访问
if(vis[n])
return; // 如果终点已经访问过,直接返回
for(int i=head[x];~i;i=e[i].next){ // 遍历与当前点相连的边
int v=e[i].to;
if(vis[v])
continue; // 如果该边已访问过,跳过当前循环
if(dis[v]<min(dis[x],e[i].w)){ // 如果该边的距离小于当前点的距离
dis[v]=min(dis[x],e[i].w); // 更新距离
q.push(make_pair(dis[v],v)); // 将该点压入队列
}
}
}
}
int main(){
int p=1;
scanf("%d", &T); // 输入测试用例的数量
while(T--){
cnt=0; // 初始化 cnt 为 0
memset(head,-1,sizeof(head)); // 初始化 head 数组为 -1
scanf("%d%d", &n, &m); // 输入点的数量和边的数量
int u,v,w;
for(int i=1;i<=m;i++){
scanf("%d%d%d", &u, &v, &w); // 输入每一条边的信息
add(u,v,w);//两条边
add(v,u,w);
}
solve(1); // 调用 solve 函数,求解最小值最大路径
cout<<"Scenario #"<<p++<<":"<<endl;
cout<<dis[n]<<endl<<endl; // 输出结果
}
return 0;
}
🎂货币兑换 -- Bellman
1860 -- Currency Exchange (poj.org)
解释
虽然但是,我觉得题目可能忽略了这种情况(题目也没有说明,所有货币一定可以互相兑换好像),假设存在正环,但是从起点(初始持有种类)无法到达正环的情况,这个没有特判.......?
转化为 判正环? -- Bellman
货币种类? --? 顶点,兑换规则? --? 边
所以? -->? n 个点,m 条边,源点 s
dis[i] 表示从起点 s 出发到 点 i 剩余的最大金额
v 表示起点 s 初始具有的金额,dis[s] = v(即源点 到 自己 剩余的最大金额)
于是,我们创建个结构体,采用 边集数组 存图
struct node{
int a,b;//a:起点;b:终点
double r,c;//r:汇率;c:手续费
}e[210];//可以换算成2*m,m为边数 add() 函数👇
由题可知,边为有向边(虽然一定有对应的另一条,但是汇率和手续费不一定相同)
void add(int a,int b,double r,double c){
e[cnt].a=a;
e[cnt].b=b;
e[cnt].r=r;
e[cnt++].c=c;
}后面的就是套 bellman - ford 模板,参考上面的代码,这里再贴一下👇
// 源点 u 到 其他点 的最短长度,并判断负环
bool bellman_ford(int u)
{
memset(dis, 0x3f, sizeof(dis));
dis[u] = 0;
for (int i = 1; i < n; ++i) { // 对所有边进行 n - 1 次松弛
bool flag = 0;
for (int j = 0; j < m; ++j) // m 条边
if (dis[e[j].b] > dis[e[j].a] + e[j].w) {
dis[e[j].b] = dis[e[j].a] + e[j].w; // 松弛
flag = true;
}
// 一点优化,提前结束 n - 1 次松弛
if (flag == false) return false; // 所有边松弛完了,没有负环
}
// 执行第 n 次松弛
for (int j = 0; j < m; ++j)
if (dis[e[j].b] > dis[e[j].a] + e[j].w)
return true; // 有负环
return false;
}关键一行
(a点金额?- 佣金) * 汇率 = b 点金额
// 起点 a, 终点 b, a 到 b 汇率r, 佣金c // (a金额 - 佣金) * 汇率 = b金额 if ( dis[e[j].b] < (dis[e[j].a] - e[j].c) * e[j].r ) dis[e[j].b] = (dis[e[j].a] - e[j].c) * e[j].r;能赚就更新(环的正负,可以根据需要修改 > 或?< 号)
坑点
(1)边数是 2m,因为每读入两个点和之间的汇率,都是双向的,虽然数据不一样
(2)r 汇率,c 佣金,都是 double,所以所有涉及到 r, c 的地方,都要用 double 生命,包括 1)函数参数,2)全局变量,?3)结构体里
AC 代码
#include<iostream>
using namespace std;
// n 个点,m 条边,源点 s,边计数 cnt
int n, m, s, cnt = 0;
double v, dis[110];
struct node {
int u, v;
double r, c;
}e[210]; // 每个点只能兑换 2 种货币,即 2 点之间最多 2 条边
// 100 个点最多 200 条边
void add(int u, int v, double r, double c)
{
e[cnt].u = u;
e[cnt].v = v;
e[cnt].r = r; // 汇率
e[cnt++].c = c; // 佣金
}
bool bellman()
{
dis[s] = v; // 源点剩余最大金额
// 对所有边进行 n - 1 次松弛
for (int i = 1; i < n; ++i) {
bool flag = 0;
// 2m 条边
for (int j = 0; j < 2*m; ++j) // 注意!j < 2*m 或 j < cnt
if ( dis[e[j].v] < (dis[e[j].u] - e[j].c) * e[j].r ) {
dis[e[j].v] = (dis[e[j].u] - e[j].c) * e[j].r;
flag = true;
}
if (flag == false) return false; // 没有更新, 不存在正环
}
// 第 n 次松弛
for (int j = 0; j < 2*m; ++j) // 2*m 不是 m
if ( dis[e[j].v] < (dis[e[j].u] - e[j].c) * e[j].r )
return true; // 还可以松弛, 说明有正环
return false;
}
int main()
{
cin >> n >> m >> s >> v;
int a, b; // 起点, 终点
double ra, ca, rb, cb; // r 汇率,c 佣金
// 读入边
for (int i = 0; i < m; ++i) {
cin >> a >> b >> ra >> ca >> rb >> cb;
add(a, b, ra, ca);
add(b, a, rb, cb); // 2m 条边
}
if (bellman()) cout << "YES";
else cout << "NO";
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 代码重复:搞定代码重复的三个绝招
- 第25节: Vue3 带组件
- Day10学习记录
- 计组_第三章_系统总线
- 【Vulnhub 靶场】【Hack Me Please: 1】【简单】【20210731】
- 三个整数比较大小(2)
- 2024年MySQL学习指南(三),探索MySQL数据库,掌握未来数据管理趋势
- 基于JavaWeb+SSM+Vue基于微信小程序的在线投稿系统的设计和实现
- 强化学习求解TSP(七):Qlearning求解旅行商问题TSP(提供Python代码)
- 2023第三届中国高校大数据挑战赛B题代码