【leetcode100-021】【矩阵】搜索二维矩阵 II
发布时间:2023年12月26日
【题干】
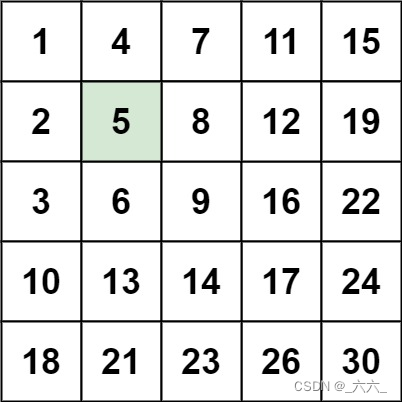
编写一个高效的算法来搜索?m?x?n?矩阵?matrix?中的一个目标值?target?。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
【思路】
以右上角为起点斜着看这个矩阵,会发现,这是一颗二叉搜索树。
那么我们就从右上角(0,n?1)处开始搜索。
在每一步的搜索过程中,如果我们位于位置(x,y),那么我们希望在以matrix 的左下角为左下角、以(x,y) 为右上角的矩阵中进行搜索,即行的范围为[x,m?1],列的范围为[0,y]:
- 如果matrix[x,y]=target,说明搜索完成;
- 如果matrix[x,y]>target,由于每一列的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第y列的元素都是严格大于target的,y--;
- 如果matrix[x,y]<target,由于每一行的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第x行的元素都是严格小于target的,x++;
- 在搜索的过程中,如果我们超出了矩阵的边界,那么说明矩阵中不存在target。
【题解】
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int x = 0, y = n - 1;
while (x < m && y >= 0) {
if (matrix[x][y] == target) {
return true;
}
if (matrix[x][y] > target) {
--y;
}
else {
++x;
}
}
return false;
}
};
文章来源:https://blog.csdn.net/weixin_63059689/article/details/135222353
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!