数据结构及单链表例题(下)

上次我们已经了解了单链表的数据结构定义以及创建单链表的两种方法,这节介绍几道例题.

前言

一、已知L为带头结点的单链表,请依照递归思想实现下列运算

二、单链表访问第i个数据节点

三、在第i个元素前插入元素e

四、删除第i个结点

五、查找带头结点单链表倒数第m个结点并输出(m<链的长度)

六、设单链表表头指针为L,节点数据域为数字(0~9)(字符的思想一样),设计时间复杂度最低的算法判断前n/2个数字是否与后n/2数字一次相同(说人话就是是否前后一样)

?七、从非递减有序的单链表中删除值相同的多余元素

八、设有一个非递减正整数单链表(有重复数)设计算法确定比x小的节点数量

九、删除非递减单链表La中La与Lb相同元素(算法实现了但没验证)

十、已知La,Lb,Lc是三个链表,且他们已经初始化,其元素按递增顺序排序每个表中均无重复数据,设计算法在表Lc中,删除同时出现在La和Lb中的所有元素.(算法实现了但没验证)

十一、带头节点单链表中的所有元素的数据按递增顺序排列,删除链表中大于min且小于max的元素

十二、对链表进行冒泡排序

十三、设L为单链表头节点地址,其数据节点都是正整数可能存在相同的数值的节点,设计一个空间复杂度最低的算法利用直接插入排序把该链表按递增排序,并将重复点删除.

十四、给定两个单链表,编写算法找出两个链表的公共节点(算法实现没验证)

总代码与测试结果

总结

---

前言

这节课介绍的几道例题是考试中常考的大家应好好理解,我将注释写清楚点.单链表的数据结构定义与头插法和尾插法创建单链表在上节已经实现这节课主要做几道例题,但要想测试例题需要建立单链表,所以大家可以在最后的总代码和结果中查看.其中文章中备注的算法实现了但未验证不代表算法是错的,只是由于实现的前提条件比较困难.

一、已知L为带头结点的单链表,请依照递归思想实现下列运算

1. 求链表中的最大整数
2. 求表中的节点数
3. 求链表所有元素的平均值

求链表中的最大整数

//(1)求链表中的最大整数
int getmax(Linklist L) {
	if (L == NULL) {
		return MIN;//宏定义MIN为一个很小的数例如-999999
	}
	int tmp = getmax(L->next);//获得下一个元素
	return tmp > L->data ? tmp : L->data;//比较两个元素大小
}

这道题要熟悉了解递归

求表中的节点数

//(2)求表中的节点数
int getnodes(Linklist L) {
	if (L == NULL) {
		return 0;//没有节点了返回0
	}
	return 1 + getnodes(L->next);//求和
}

求链表所有元素的平均值

//定义求链表所有元素之和函数
float sum(Linklist L) {//递归求和函数
	if (L == NULL) {
		return 0;
	}
	return L->data + sum(L->next);
}
void operation(Linklist L) {
	int max = getmax(L->next);//带头节点传入第一个数据域
	printf("链表中的最大值为:%d\n", max);
	int num = getnodes(L->next);//带头节点传入第一个数据域
	printf("链表中的节点个数为:%d\n", num);
	float sumnum = sum(L->next);
	printf("链表中元素的和为:%f\n", sumnum);
	float avg = sumnum / num;//总和除以总结点个数
	printf("链表元素的平均值为:%.4lf\n", avg);
}

二、单链表访问第i个数据节点

void getElem(Linklist L, int i, int& e) {
	int j = 0;//计数器
	LNode* p = L;
	while (NULL != p->next) {
		j++;
		if (j == i) {//到第i个节点将值赋给e返回
			e = p->next->data;
			break;
		}
		p = p->next;
	}
}

三、在第i个元素前插入元素e

//例5:在第i个元素前插入元素e
void insertElem(Linklist L, int i, int e) {
	int j = 0;
	LNode* p = L->next;
	LNode* pre = L;//前驱指针
	while (p != NULL) {
		j++;
		if (j == i) {
			LNode* pNode = (LNode*)malloc(sizeof(LNode));
			assert(pNode);
			pNode->data = e;
			pNode->next = pre->next;
			pre->next = pNode;
			break;
		}
		pre = p;
		p = p->next;
	}

}

在单链表插入元素,需要找到插入位置元素的前驱.

核心代码

pNode->next = pre->next;
pre->next = pNode;

四、删除第i个结点

//删除第i个结点
void deleteElem(Linklist L, int i, int &e) {
	int j = 0;
	LNode* p = L->next;
	LNode* pre = L;
	while (p != NULL) {
		j++;
		if (j == i) {
			e = p->data;
			LNode* tmp = p;
			pre->next = p->next;//断链,删除元素的前驱节点指向删除节点的后驱
			free(tmp);//释放结点
			tmp = NULL;
			break;
		}
		pre = p;
		p = p->next;
	}
}

删除节点要释放节点使用free()

五、查找带头结点单链表倒数第m个结点并输出(m<链的长度)

//例6:查找带头结点单链表倒数第m个结点并输出(m<链的长度)
void getData(int m, Linklist L) {
	int j = 0;
	LNode* p = L->next;
	LNode* q = L->next;
	while (p != NULL) {
		j++;
		if (j == m) {
			break;
		}
		p = p->next;
	}
	if (p != NULL) {
		p = p->next;//指向下一个m+1个节点
	}
	while (p != NULL) {
		p = p->next;
		q = q->next;
	}
	if (q != NULL) {
		printf("倒数第%d个元素为:%d\n", m, q->data);
	}
}

查找倒数第m个节点挺常考的,但是也比较简单,知道思想问题就迎刃而解了.

算法思想:定义一个p指针和q指针同时指向首元素,使用指针p寻找第m+1个元素,这样就保证了p指针到q指针之间有m个元素,之后将p,q指针同时往后移这样当p指针为空时,q正好指向倒数第m个元素.

六、设单链表表头指针为L,节点数据域为数字(0~9)(字符的思想一样),设计时间复杂度最低的算法判断前n/2个数字是否与后n/2数字一次相同(说人话就是是否前后一样)

int isSym(Linklist L,int n) {
	int j = 0;
	LNode* p = L->next;
	LNode* q = L->next;
	while (p != NULL) {
		j++;
		if (j == n / 2) {
			break;
		}
		p = p->next;
	}
	if (n % 2 == 0) {//偶数移一位
		p = p->next;
	}
	else {//奇数移两位
		p = p->next->next;
	}
	while (p != NULL) {
		if (q->data != p->data) {
			return 0;
		}
		p = p->next;
		q = q->next;
	}
	return 1;
}

算法思想:前一半和后一半是否一样只需找到后一半的首元素,找到后只需将前一半与后一般元素一一比较即可.但中间有个细节就是链表的长度是奇数还是偶数,分情况讨论.这里我画个图方便大家理解.

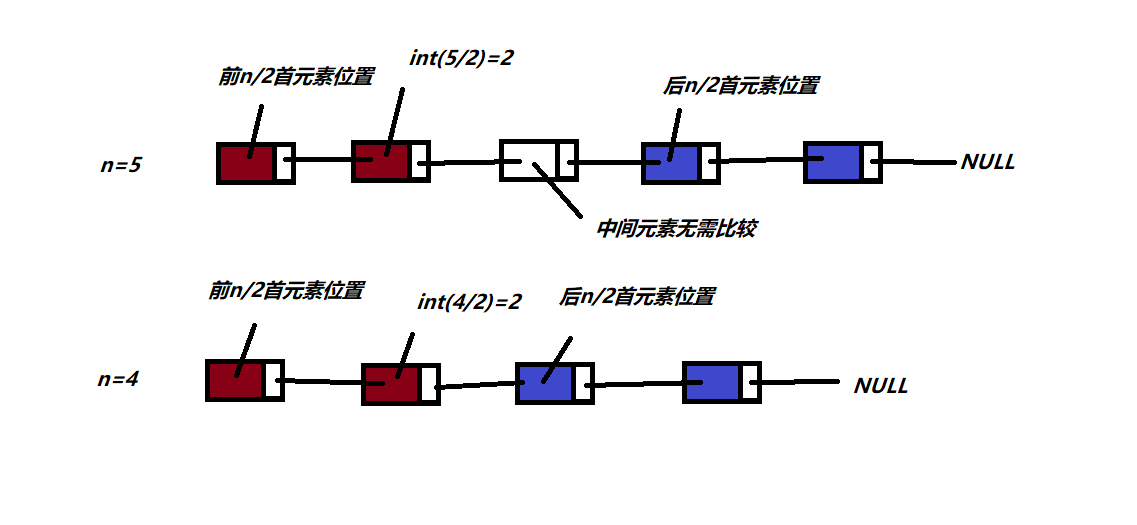
?七、从非递减有序的单链表中删除值相同的多余元素

//例8:从非递减有序的单链表中删除值相同的多余元素
void deletesimilar(Linklist L) {
	LNode* preNode = L->next;
	while (preNode!=NULL && NULL != preNode->next) {
		if (preNode->next->data == preNode->data) {
			LNode* p = preNode->next;
			preNode->next = p->next;
			free(p);
			p = NULL;
		}
		else {
			preNode = preNode->next;
		}

	}
}

这道题也非常静经典.

算法思想:从非递减链表中删除重复元素只需遍历元素与前驱元素比较,如果相等就删除节点.大家只要知道思想代码就可以灵活多变.

八、设有一个非递减正整数单链表(有重复数)设计算法确定比x小的节点数量

//例9:设有一个非递减正整数单链表(有重复数)设计算法确定比x小的节点数量
//L:{1,2,2,2,4,6}比4小的节点有2个
int lessNodes(Linklist L, int x) {
	int i = 0;
	LNode* preCur = L;
	LNode* pCur = L->next;
	while (pCur != NULL && pCur->data < x) {
		if (pCur->data != preCur->data) {
			i++;
		}
		preCur = pCur;
		pCur = pCur->next;
	}
	return i;
}

这道题与上道题类似.

算法思想:非递减有重复数,查找比x节点有几个(去掉重复),遍历元素只要当前元素小于x且不等于前驱元素,也就是说出现了新的值,计数器i就++,最后返回i,这道题也就是上道题的变形,思想很重要,可以帮助你解决很多问题.

九、删除非递减单链表La中La与Lb相同元素(算法实现了但没验证)

//例10:删除非递减单链表La中La与Lb相同元素(算法实现了但没验证)
void delsimilar(Linklist La, Linklist Lb) {//在A表上进行修改
	LNode* preCurA = La;
	LNode* pCurA = La->next;
	LNode* pCurB = Lb->next;
	while (pCurA && pCurB) {
		if (pCurA->data < pCurB->data) {//说明与B相等元素在后面,移动A指针
			preCurA = pCurA;//因为在A表上修改记录前驱
			pCurA = pCurA->next;
		}
		else if (pCurA->data > pCurB->data) {说明与A相等元素在后面,移动B指针
			pCurB = pCurB->next;
		}
		else {//相等删除A中当前元素
			preCurA = pCurA->next;
			free(pCurA);
			pCurA = preCurA->next;
		}
	}
}

这道题也比较经典.

算法思想:LA非递减删除LB相同元素,设定两个指针p和q,p指向表A中元素,q指向表B中元素,如果有一方的当前指针指向的元素比另一方小则移动该链表的指针,因为如果想要找到相等的只能在后面元素里面找.

十、已知La,Lb,Lc是三个链表,且他们已经初始化,其元素按递增顺序排序每个表中均无重复数据,设计算法在表Lc中,删除同时出现在La和Lb中的所有元素.(算法实现了但没验证)

//例11:已知La,Lb,Lc是三个链表,且他们已经初始化,其元素按递增顺序排序每个表中均无重复数据,设计算法在表Lc中
//删除同时出现在La和Lb中的所有元素.(算法实现了但没验证)
void deleteOper(LNode*& preCur, LNode*& pCur, ElemType e) {
	while (NULL != pCur && pCur->data < e) {//找到第一个>=e的元素
		preCur = pCur;
		pCur = pCur->next;
	}
	if (pCur!=NULL && e == pCur->data) {//如果等于该元素删除
		preCur = pCur->next;
		free(pCur);
		pCur = preCur->next;
	}
}
void delsimilar2(Linklist La, Linklist Lb, Linklist Lc) {
	LNode* pCurA = La->next;
	LNode* pCurB = Lb->next;
	LNode* preCurC = Lc;
	LNode* pCurC = Lc->next;
	while (pCurA && pCurB) {//寻找LA与LB中相同的元素
		if (pCurA->data < pCurB->data) {
			pCurA = pCurA->next;
		}
		else if(pCurA->data > pCurB->data){
			pCurB = pCurB->next;
		}
		else {
			deleteOper(preCurC, pCurC, pCurA->data);
			pCurB = pCurB->next;
			pCurA = pCurA->next;
		}
	}
}

算法思想:这道题是上一道题的增强版,但是也是比较简单的,就是找LA与LB中相同的元素再去LC表中查找并删除即可.注意一个细节,由于不想从头开始找,所以Lc记录的前驱节点为引用传递,这其实是c++的语法,你可以改为指针,进行址传递,但考试时写伪代码即可.

十一、带头节点单链表中的所有元素的数据按递增顺序排列,删除链表中大于min且小于max的元素

//例12:带头节点单链表中的所有元素的数据按递增顺序排列,删除链表中大于min且小于max的元素
void deleteNodes(Linklist L,int min ,int max) {
	LNode* preCur = L;
	LNode* pCur = L->next;
	while (pCur) {//找到第一个大于min的节点
		if (min < pCur->data) {
			break;
		}
		preCur = pCur;
		pCur = pCur->next;
	}
	while (pCur && pCur->data < max) {//一直删除到大于max
		preCur->next = pCur->next;
		free(pCur);
		pCur = preCur->next;
	}
}

这个比较简单了遍历一次链表就可以了,但要记住删除单链表节点一定要记录前驱节点.

十二、对链表进行冒泡排序

//例13:对链表进行冒泡排序
void bubleSort(Linklist L) {
	while (1) {//每次都从第一个元素开始遇到大于的就交换
		int isExchange = 0;//记录是否元素发生交换
		LNode* p = L->next;
		while (p && p->next) {
			if (p->data > p->next->data) {//交换元素
				ElemType tmp = p->data;
				p->data = p->next->data;
				p->next->data = tmp;
				isExchange = 1;
			}
			p = p->next;
		}
		if (isExchange == 0) {//当前这一次排序没发生交换说明排序已经完成
			break;
		}
	}
}

算法思想:就是冒泡排序的思想这里不用交换节点直接交换数据即可.要注意与数组的冒泡排序不同由于链表在开始前无法知道元素个数,所以用while(1),结束条件就是当链表中不在发生交换说明排序以完成.后续我们在排序算法时还会提及.

十三、设L为单链表头节点地址,其数据节点都是正整数可能存在相同的数值的节点,设计一个空间复杂度最低的算法利用直接插入排序把该链表按递增排序,并将重复点删除.

//例14:设L为单链表头节点地址,其数据节点都是正整数可能存在相同的数值的节点,设计一个空间复杂度最低的算法利用直接插入排序
//把该链表按递增排序,并将重复点删除.
void insertsort(Linklist L) {
	LNode* p = L->next;//先把表提出来
	L->next = NULL;
	while (p != NULL) {
		LNode* preCur = L;
		LNode* pCur = L->next;
		while (pCur && pCur->data < p->data) {//寻找插入位置
			preCur = pCur;
			pCur = pCur->next;
		}
		LNode* tmp = p;//先记录元素节点
		p = p->next;//指针向后
		if (pCur!=NULL && pCur->data == tmp->data) {//如果第一个不小于该元素等于该元素删除节点
			free(tmp);
			tmp = NULL;
		}
		else {//插入节点
			tmp->next = preCur->next;
			preCur->next = tmp;
		}
	}
}

算法思想:采用直接插入排序,这里对直接插入排序不理解的直接跳过即可,这题主要一个思想就是对链表操作时可以将链表断开之后一个元素一个元素的进行操作.

十四、给定两个单链表,编写算法找出两个链表的公共节点(算法实现没验证)

//例15:给定两个单链表,编写算法找出两个链表的公共节点(算法实现没验证)
//定义求链表长度函数
int Length(Linklist L) {
	LNode* p = L->next;
	int length = 0;
	while (p!=NULL) {
		length++;
		p = p->next;
	}
	return length;
}
//寻找公共节点函数
//思想:公共节点只可能在短链的后面节点出现,故长链前的节点不用比较
LNode* search(Linklist La, Linklist Lb) {
	int Lalength = Length(La);
	int Lblength = Length(Lb);
	int dist = 0;
	LNode* shortlist = NULL;
	LNode* longlist = NULL;
	if (Lalength > Lblength) {
		longlist = La->next;
		shortlist = Lb->next;
		dist = Lalength - Lblength;
	}
	else {
		longlist = Lb->next;
		shortlist = La->next;
		dist = Lblength - Lalength;
	}
	while (dist--) {//寻找可能出现公共节点的第一个节点
		longlist = longlist->next;
	}
	while (longlist!=NULL) {//节点依次比较
		if (longlist == shortlist) {
			return longlist;
		}
		else {
			longlist = longlist->next;
			shortlist = shortlist->next;
		}
	}
	return NULL;
}

这道题王道辅导书上的课后题也有.

算法思想:要寻找两个链表的公共节点,第一个公共节点只能在长链中长链长度减短链长度之后.这里简单画个图帮助大家理解.

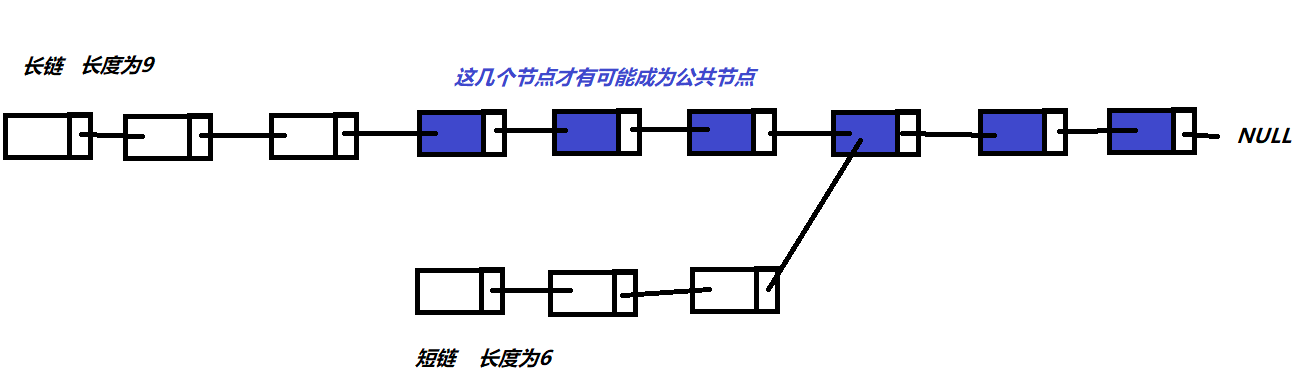
总代码与测试结果

测试结果有标注对应好.

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<malloc.h>

#define MIN -999999;
typedef int ElemType;

//单链表的数据结构定义
typedef struct LNode {
	ElemType data;//数据
	struct LNode* next;//下一个节点
}LNode,*Linklist;
//使用头插法建立单链表
void CreateLinklist1(Linklist &L,int arr[],int arrlength) {
	L = (LNode*)malloc(sizeof(LNode));//申请一个头节点
	assert(L);
	L->next = NULL;
	for (int i = 0; i < arrlength; i++) {
		LNode*pNode = (LNode*)malloc(sizeof(LNode));
		assert(pNode);
		pNode->data = arr[i];
		pNode->next = L->next;
		L->next = pNode;
	}
}
//使用尾插法建立单链表
void CreateLinklist2(Linklist& L,int arr[],int arrlength) {
	L = (LNode*)malloc(sizeof(LNode));//申请一个头节点
	assert(L);
	L->next = NULL;
	LNode* pTail = L;
	for (int i = 0; i < arrlength; i++) {
		LNode* pNode = (LNode*)malloc(sizeof(LNode));
		assert(pNode);
		pNode->data = arr[i];
		pNode->next = pTail->next;
		pTail->next = pNode;
		pTail = pNode;
	}
}
//打印单链表函数
void print(Linklist L) {
	LNode* p = L->next;
	while (NULL != p) {
		printf("%d ", p->data);
		p = p->next;
	}
	printf("\n");
}
//例3:已知L为带头结点的单链表,请依照递归思想实现下列运算
//(1)求链表中的最大整数
int getmax(Linklist L) {
	if (L == NULL) {
		return MIN;
	}
	int tmp = getmax(L->next);
	return tmp > L->data ? tmp : L->data;
}
//(2)求表中的节点数
int getnodes(Linklist L) {
	if (L == NULL) {
		return 0;
	}
	return 1 + getnodes(L->next);
}
//(3)求链表所有元素的平均值
//定义求链表所有元素之和函数
float sum(Linklist L) {
	if (L == NULL) {
		return 0;
	}
	return L->data + sum(L->next);
}
void operation(Linklist L) {
	int max = getmax(L->next);//带头节点传入第一个数据域
	printf("链表中的最大值为:%d\n", max);
	int num = getnodes(L->next);//带头节点传入第一个数据域
	printf("链表中的节点个数为:%d\n", num);
	float sumnum = sum(L->next);
	printf("链表中元素的和为:%f\n", sumnum);
	float avg = sumnum / num;
	printf("链表元素的平均值为:%.4lf\n", avg);
}
//例4:单链表访问第i个数据节点
void getElem(Linklist L, int i, int& e) {
	int j = 0;
	LNode* p = L;
	while (NULL != p->next) {
		j++;
		if (j == i) {
			e = p->next->data;
			break;
		}
		p = p->next;
	}
}
//例5:在第i个元素前插入元素e
void insertElem(Linklist L, int i, int e) {
	int j = 0;
	LNode* p = L->next;
	LNode* pre = L;
	while (p != NULL) {
		j++;
		if (j == i) {
			LNode* pNode = (LNode*)malloc(sizeof(LNode));
			assert(pNode);
			pNode->data = e;
			pNode->next = pre->next;
			pre->next = pNode;
			break;
		}
		pre = p;
		p = p->next;
	}

}
//删除第i个结点
void deleteElem(Linklist L, int i, int &e) {
	int j = 0;
	LNode* p = L->next;
	LNode* pre = L;
	while (p != NULL) {
		j++;
		if (j == i) {
			e = p->data;
			LNode* tmp = p;
			pre->next = p->next;//断链
			free(tmp);//释放结点
			tmp = NULL;
			break;
		}
		pre = p;
		p = p->next;
	}
}
//例6:查找带头结点单链表倒数第m个结点并输出
void getData(int m, Linklist L) {
	int j = 0;
	LNode* p = L->next;
	LNode* q = L->next;
	while (p != NULL) {
		j++;
		if (j == m) {
			break;
		}
		p = p->next;
	}
	if (p != NULL) {
		p = p->next;//指向下一个m+1个节点
	}
	while (p != NULL) {
		p = p->next;
		q = q->next;
	}
	if (q != NULL) {
		printf("倒数第%d个元素为:%d\n", m, q->data);
	}
}
//例7:设单链表表头指针为L,节点数据域为数字(0~9)(字符的思想一样),设计时间复杂度最低的算法判断前n/2
//个数字是否与后n/2数字一次相同(说人话就是是否前后一样)
int isSym(Linklist L,int n) {
	int j = 0;
	LNode* p = L->next;
	LNode* q = L->next;
	while (p != NULL) {
		j++;
		if (j == n / 2) {
			break;
		}
		p = p->next;
	}
	if (n % 2 == 0) {
		p = p->next;
	}
	else {
		p = p->next->next;
	}
	while (p != NULL) {
		if (q->data != p->data) {
			return 0;
		}
		p = p->next;
		q = q->next;
	}
	return 1;
}
//例8:从非递减有序的单链表中删除值相同的多余元素
void deletesimilar(Linklist L) {
	LNode* preNode = L->next;
	while (preNode!=NULL && NULL != preNode->next) {
		if (preNode->next->data == preNode->data) {
			LNode* p = preNode->next;
			preNode->next = p->next;
			free(p);
			p = NULL;
		}
		else {
			preNode = preNode->next;
		}

	}
}
//例9:设有一个非递减正整数单链表(有重复数)设计算法确定比x小的节点数量
//L:{1,2,2,2,4,6}比4小的节点有2个
int lessNodes(Linklist L, int x) {
	int i = 0;
	LNode* preCur = L;
	LNode* pCur = L->next;
	while (pCur != NULL && pCur->data < x) {
		if (pCur->data != preCur->data) {
			i++;
		}
		preCur = pCur;
		pCur = pCur->next;
	}
	return i;
}
//例10:删除非递减单链表La中La与Lb相同元素(算法实现了但没验证)
void delsimilar(Linklist La, Linklist Lb) {
	LNode* preCurA = La;
	LNode* pCurA = La->next;
	LNode* pCurB = Lb->next;
	while (pCurA && pCurB) {
		if (pCurA->data < pCurB->data) {
			preCurA = pCurA;
			pCurA = pCurA->next;
		}
		else if (pCurA->data > pCurB->data) {
			pCurB = pCurB->next;
		}
		else {
			preCurA = pCurA->next;
			free(pCurA);
			pCurA = preCurA->next;
		}
	}
}
//例11:已知La,Lb,Lc是三个链表,且他们已经初始化,其元素按递增顺序排序每个表中均无重复数据,设计算法在表Lc中
//删除同时出现在La和Lb中的所有元素.(算法实现了但没验证)
void deleteOper(LNode*& preCur, LNode*& pCur, ElemType e) {
	while (NULL != pCur && pCur->data < e) {
		preCur = pCur;
		pCur = pCur->next;
	}
	if (pCur!=NULL && e == pCur->data) {
		preCur = pCur->next;
		free(pCur);
		pCur = preCur->next;
	}
}
void delsimilar2(Linklist La, Linklist Lb, Linklist Lc) {
	LNode* pCurA = La->next;
	LNode* pCurB = Lb->next;
	LNode* preCurC = Lc;
	LNode* pCurC = Lc->next;
	while (pCurA && pCurB) {
		if (pCurA->data < pCurB->data) {
			pCurA = pCurA->next;
		}
		else if(pCurA->data > pCurB->data){
			pCurB = pCurB->next;
		}
		else {
			deleteOper(preCurC, pCurC, pCurA->data);
			pCurB = pCurB->next;
			pCurA = pCurA->next;
		}
	}
}
//例12:带头节点单链表中的所有元素的数据按递增顺序排列,删除链表中大于min且小于max的元素
void deleteNodes(Linklist L,int min ,int max) {
	LNode* preCur = L;
	LNode* pCur = L->next;
	while (pCur) {//找到第一个大于min的节点
		if (min < pCur->data) {
			break;
		}
		preCur = pCur;
		pCur = pCur->next;
	}
	while (pCur && pCur->data < max) {//一直删除到大于max
		preCur->next = pCur->next;
		free(pCur);
		pCur = preCur->next;
	}
}
//例13:对链表进行冒泡排序
void bubleSort(Linklist L) {
	while (1) {//每次都从第一个元素开始遇到大于的就交换
		int isExchange = 0;
		LNode* p = L->next;
		while (p && p->next) {
			if (p->data > p->next->data) {
				ElemType tmp = p->data;
				p->data = p->next->data;
				p->next->data = tmp;
				isExchange = 1;
			}
			p = p->next;
		}
		if (isExchange == 0) {
			break;
		}
	}
}
//例14:设L为单链表头节点地址,其数据节点都是正整数可能存在相同的数值的节点,设计一个空间复杂度最低的算法利用直接插入排序
//把该链表按递增排序,并将重复点删除.
void insertsort(Linklist L) {
	LNode* p = L->next;
	L->next = NULL;
	while (p != NULL) {
		LNode* preCur = L;
		LNode* pCur = L->next;
		while (pCur && pCur->data < p->data) {//寻找插入位置
			preCur = pCur;
			pCur = pCur->next;
		}
		LNode* tmp = p;
		p = p->next;
		if (pCur!=NULL && pCur->data == tmp->data) {//如果第一个不小于该元素等于该元素删除节点
			free(tmp);
			tmp = NULL;
		}
		else {//插入节点
			tmp->next = preCur->next;
			preCur->next = tmp;
		}
	}
}
//例15:给定两个单链表,编写算法找出两个链表的公共节点(算法实现没验证)
//定义求链表长度函数
int Length(Linklist L) {
	LNode* p = L->next;
	int length = 0;
	while (p!=NULL) {
		length++;
		p = p->next;
	}
	return length;
}
//寻找公共节点函数
//思想:公共节点只可能在短链的后面节点出现,故长链前的节点不用比较
LNode* search(Linklist La, Linklist Lb) {
	int Lalength = Length(La);
	int Lblength = Length(Lb);
	int dist = 0;
	LNode* shortlist = NULL;
	LNode* longlist = NULL;
	if (Lalength > Lblength) {
		longlist = La->next;
		shortlist = Lb->next;
		dist = Lalength - Lblength;
	}
	else {
		longlist = Lb->next;
		shortlist = La->next;
		dist = Lblength - Lalength;
	}
	while (dist--) {//寻找可能出现公共节点的第一个节点
		longlist = longlist->next;
	}
	while (longlist!=NULL) {//节点依次比较
		if (longlist == shortlist) {
			return longlist;
		}
		else {
			longlist = longlist->next;
			shortlist = shortlist->next;
		}
	}
	return NULL;
}
int main() {
	Linklist L=NULL;
	int arr[10] = { 1,50,88,49,66,13,12,17,19,44 };
	int arrlength = sizeof(arr) / sizeof(arr[0]);
	//使用头插法建立单链表
	CreateLinklist2(L, arr, arrlength);
	printf("输出尾插法链中序列L:");
	print(L);
	printf("**************************************\n");
	printf("对例3进行测试!\n");
	operation(L);
	printf("**************************************\n");
	printf("对例4进行测试!\n");
	int e = 0;
	getElem(L, 4, e);
	printf("e的值为:%d\n", e);
	int a = 777;
	printf("**************************************\n");
	printf("对例5进行测试!\n");
	insertElem(L, 4, a);
	print(L);
	printf("删除第i个节点!\n");
	int b = 0;
	deleteElem(L, 4, b);
	printf("b的值为:%d\n", b);
	print(L);
	printf("**************************************\n");
	printf("对例6进行测试!\n");
	getData(4,L);
	printf("**************************************\n");
	printf("对例7进行测试!\n");
	Linklist La;
	int arr1[11] = { 1,2,3,4,5,6,1,2,3,4,5 };
	int arrlength1 = sizeof(arr1) / sizeof(arr1[0]);
	//使用头插法建立单链表
	CreateLinklist2(La, arr1, arrlength1);
	print(La);
	printf("判断单链表是否对称(是返回1不是为0):%d\n", isSym(La, 11));
	printf("**************************************\n");
	printf("对例8进行测试!\n");
	Linklist Lb;
	int arr2[10] = { 1,1,2,2,3,3,4,4,5,6};
	int arrlength2 = sizeof(arr2) / sizeof(arr2[0]);
	//使用头插法建立单链表
	CreateLinklist2(Lb, arr2, arrlength2);
	printf("删除前:");
	print(Lb);
	deletesimilar(Lb);
	printf("删除后:");
	print(Lb);
	printf("**************************************\n");
	printf("对例9进行测试!\n");
	CreateLinklist2(Lb, arr2, arrlength2);
	printf("比4小的节点个数为:%d\n", lessNodes(Lb, 4));
	printf("**************************************\n");
	printf("对例12进行测试!\n");
	print(Lb);
	deleteNodes(Lb,2,6);
	print(Lb);
	printf("**************************************\n");
	printf("对例13进行测试!\n");
	print(L);
	bubleSort(L);
	print(L);
	printf("**************************************\n");
	printf("对例14进行测试!\n");
	CreateLinklist2(L, arr, arrlength);
	print(L);
	insertsort(L);
	print(L);
	printf("**************************************\n");
	printf("对例15进行测试!\n");
	printf("链表长度为:%d",Length(L));
	return 0;
}

---

总结

几道关于单链表的题目,希望可以帮助大家,本人制作不易,麻烦点点赞,谢谢家人们.