决策曲线 DCA 学习
发布时间:2023年12月17日
roc回顾ROC及曲线面积汇总学习-CSDN博客
原理
P:给真阳性患者施加干预的受益值(比如用某生化指标预测某患者有癌症,实际也有,予活检,达到了确诊的目的);
L:给假阳性患者施加干预的损失值(比如预测有癌症,给做了活检,原来只是个增生,白白受了一刀);
Pi:患者i有癌症的概率,当Pi > Pt时为阳性,给予干预。
所以较为合理的干预的时机是,当且仅当Pi × P >(1 – Pi) × L,即预期的受益高于预期的损失。推导一下可得,Pi > L / ( P + L )即为合理的干预时机,于是把L / ( P + L )定义为Pi的阈值,即Pt。
但对二元的预测指标来说,如果结果是阳性,则强制Pi=1,阴性则Pi = 0。这样,二元和其他类型的指标就有了可比性。
然后我们还可用这些参数来定义真阳性(A)、假阳性(B)、假阴性(C)、真阴性(D),即:
A:Pi ≥ Pt,实际患病;
B:Pi ≥ Pt,实际不患病;
C:Pi < Pt,实际患病;
D:Pi < Pt,实际不患病。
我们有一个随机抽样的样本,A、B、C、D分别为这四类个体在样本中的比例,则A+B+C+D = 1。那么,患病率(π)就是A + C了。
原文链接:https://blog.csdn.net/weixin_41368414/article/details/123723467
实操
rm(list = ls())
library(rmda)
data("dcaData")
set.seed(123)
fit1 <- decision_curve(Cancer ~ Age + Female + Smokes, # R语言里常见的公式类型
data = dcaData,
study.design = "cohort", # 选择研究类型
bootstraps = 50 # 重抽样次数
)
# 画图
plot_decision_curve(fit1, curve.names = "fit1",
cost.benefit.axis = F, # 是否需要损失:获益比 轴
confidence.intervals = "none" # 不画可信区间
)
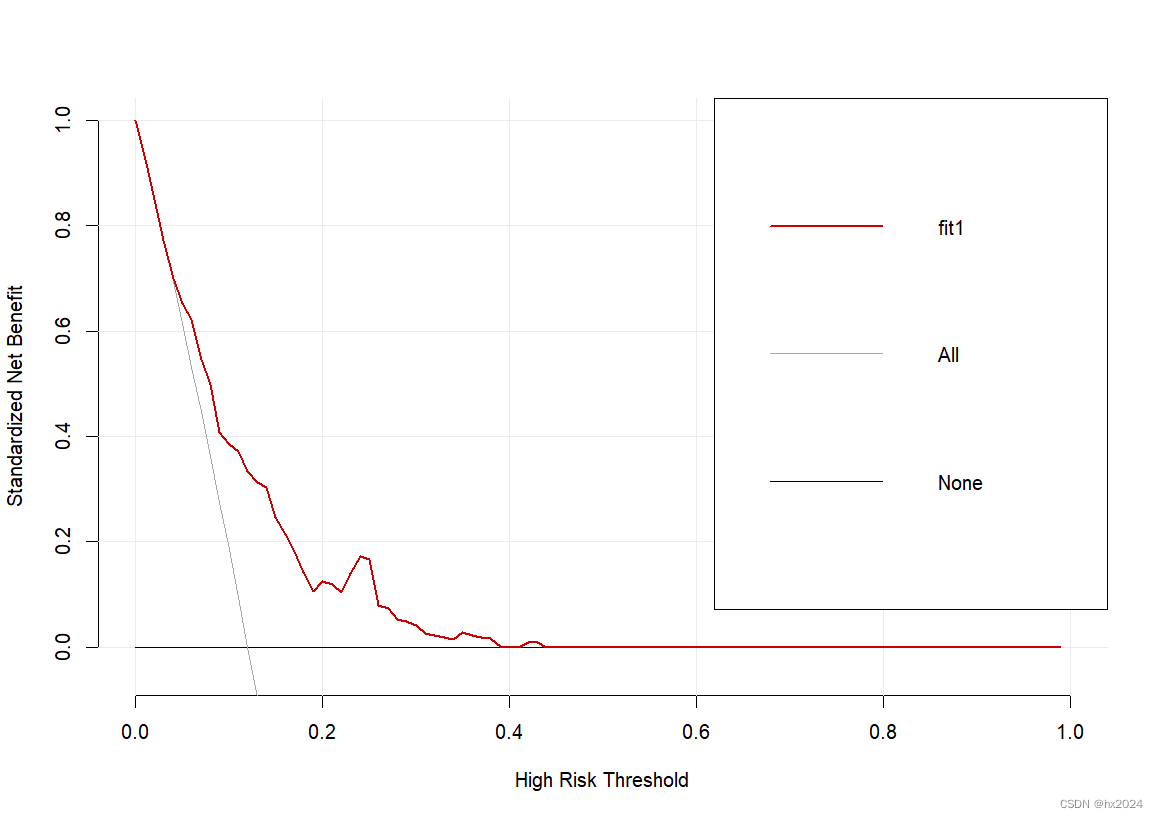
新建模型:绘制多个模型
# 新建立1个模型
set.seed(123)
fit2 <- decision_curve(Cancer~Age + Female + Smokes + Marker1 + Marker2,
data = dcaData,
bootstraps = 50
)
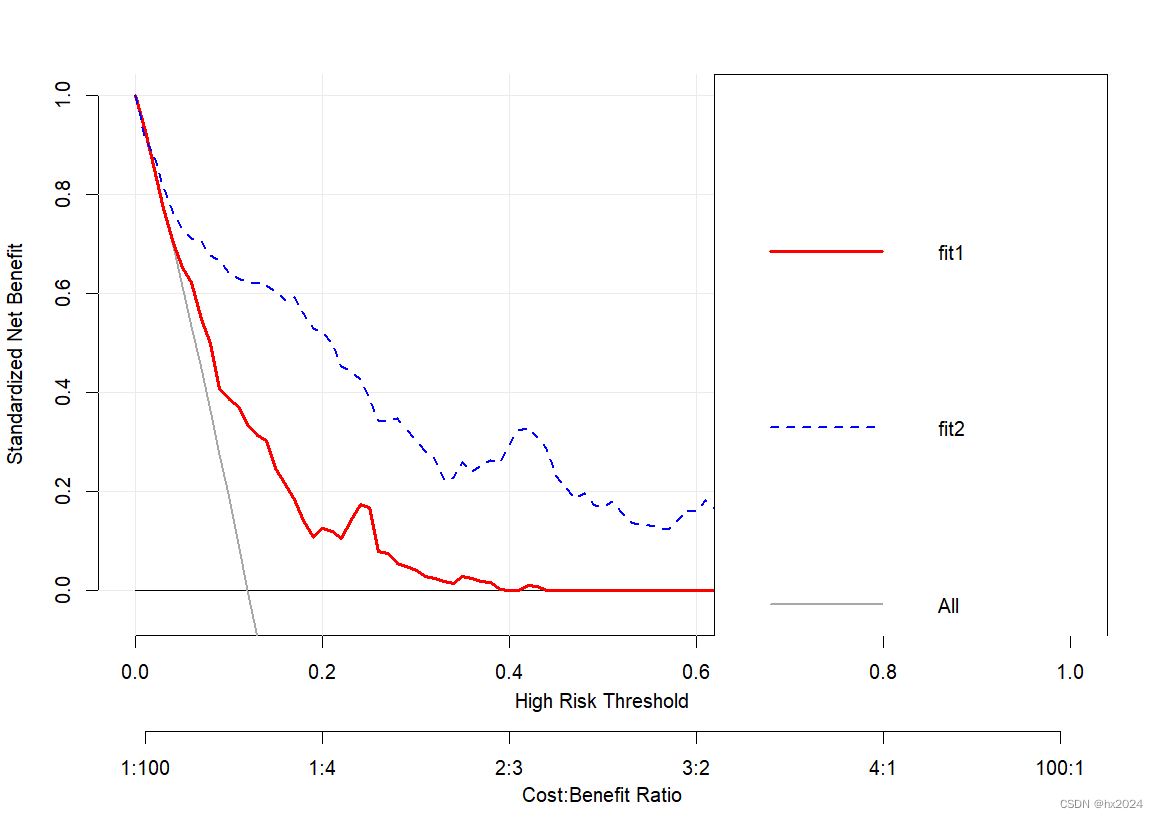
# 画图只要把多个模型放在1个列表中即可,还可以进行很多自定义调整
plot_decision_curve(list(fit1, fit2),
curve.names = c("fit1", "fit2"),
xlim = c(0, 1), # 可以设置x轴范围
legend.position = "topright", # 图例位置,
col = c("red","blue"), # 自定义颜色
confidence.intervals = "none",
lty = c(1,2), # 线型,注意顺序
lwd = c(3,2,2,1) # 注意顺序,先是自己的2个模型,然后是All,然后是None
)
参考:
文章来源:https://blog.csdn.net/hx2024/article/details/134973509
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 记录汇川:H5U与Fctory IO测试2
- MIT_线性代数笔记:第 18 讲 行列式及其性质
- JQuery的$(this)在if之后会变化
- vite + vue3 引入 three.js时引入报错
- BugKu-Web-Flask_FileUpload(模板注入与文件上传)
- 阿里云为什么是国内第一云?有哪些优势?
- 米贸搜|Facebook广告费烧得快?超出预算的钱花在哪了?怎么合理分配广告预算?
- Spring中声明Bean的注解
- 【云原生】Kubernetes Operator模式
- 新字符设备驱动中文件的私有数据