理解接雨水算法
发布时间:2024年01月10日
一、IDEA注释显示图片
在做题时,需要对照这图片,才能更好的梳理思路。
首先,注释里添加<img/>标签

之后,将鼠标光标放置在需要以阅读模式预览注释的地方,然后按快捷键Ctrl+Alt+Q即可

二、接雨水算法
先看接雨水算法的具体描述

2.1 暴力解法
我做的时候,就对着这个柱状图一直发呆,然后大概发现了思路。
我采取的是分而治之,也就是说,我依次遍历x轴,计算x所在的积水量。积水量=Min(leftMax,rightMax)-height[i]
- leftMax: 表示
x<i的height的最大值 - rightMax: 表示
x>i的height的最大值
思路有了,上代码。
class Solution {
public int trap(int[] height) {
int n = 0;
for (int i = 0; i < height.length; i++) {
int max = getMax(height, i);
int i1 = height[i];
if (max > i1) {
n += max - i1;
}
}
return n;
}
/**
* 获取i位置的左右两侧的最大值,取出最大值中的最小值
*/
public int getMax(int[] height, int i) {
if (i <= 0 || i >= height.length - 1) {
return 0;
}
int leftMax = -1, rightMax = -1;
//获取左边最大值
for (int j = i - 1; j >= 0; j--) {
int i1 = height[j];
if (i1 > leftMax) {
leftMax = i1;
}
}
//获取右边最大值
for (int j = i + 1; j < height.length; j++) {
int i1 = height[j];
if (i1 > rightMax) {
rightMax = i1;
}
}
return Math.min(leftMax, rightMax);
}
}
2.2 优化解法
这个做法的时间复杂度是O(n2),导致后面就超时了。慢就慢在,获取每个下标i最大值时,都需要去循环比较获取。能不能提前将最大值计算出来呢?其实可行的
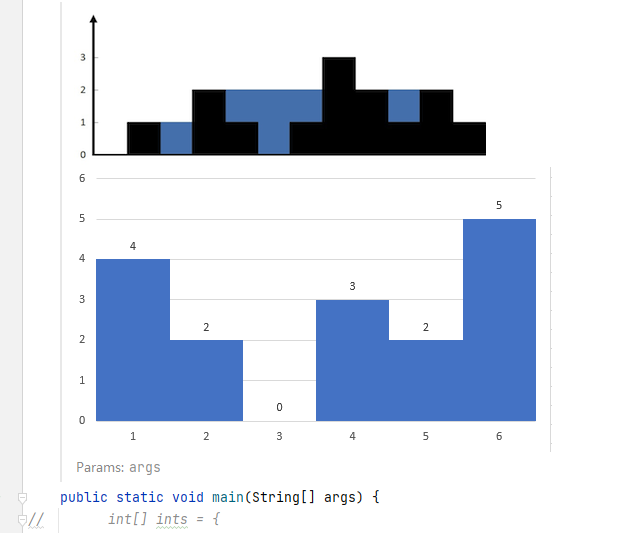
这里面其实是有规律的,以数组[4,2,0,3,2,5]为例,其对应的每个下标的leftMax和rightMax,如下图。

直接上代码,看代码理解。
class Solution {
public int trap(int[] height) {
int n = 0;
//求出每个位置的左侧最大值
int[] leftMax = new int[height.length];
for (int i = 0; i < height.length; i++) {
if (i == 0) {
leftMax[i] = 0;
} else {
leftMax[i] = Math.max(leftMax[i - 1], height[i - 1]);
}
}
//求出每个位置的右侧最大值
int[] rightMax = new int[height.length];
for (int i = height.length - 1; i >= 0; i--) {
if (i == height.length - 1) {
rightMax[i] = 0;
} else {
rightMax[i] = Math.max(rightMax[i + 1], height[i + 1]);
}
}
//每个位置的左右两侧短板值与当前位置值的差,即当前位置的积水
for (int i = 0; i < height.length; i++) {
int min = Math.min(leftMax[i], rightMax[i]);
int i1 = height[i];
if (min > i1) {
n += min - i1;
}
}
return n;
}
}
时间复杂度为O(n),太妙了。
文章来源:https://blog.csdn.net/qq_30460361/article/details/135492446
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- C语言中实现顺序表的插入、删除和更新操作(附带源码)
- MATLAB算法实战应用案例精讲-【数模应用】匈牙利算法(Kuhn-Munkres)(补充篇)(附C语言代码实现)
- 【技术科普】四大主流芯片架构及其主要优势!
- Windows系统下的可用RADIUS软件-[资源]
- openEuler操作系统的安装及免密远程连接(超详细版)
- Linux 操作系统 015-进程操作
- springMVC-数据格式化
- Unity 命令行通过python实时打印unity输出日志
- 模型之大脑和计算机的模型化
- Java面试业务场景之【 如何实现投票逻辑以确保每个用户只能投票一次,如何处理高并发情况下的投票请求?如何实时显示投票结果,如何实现转账逻辑以确保账户余额的正确更新,如何确保转账过程的安全性?】