2014,TEVC,A competitive swarm optimizer for large scale optimization(CSO)
PSO 分析(从而引入 CSO)
CSO (competitive swarm optimizer) 算法是在PSO (particle swarm optimization) 算法的基础上改进而来的。PSO算法是一种功能强大、应用广泛的群体智能算法,主要用来解决优化问题。PSO算法包含一个粒子群,粒子群里面的每个粒子均有1个 n n n维位置变量和1个 n n n维速度变量。在算法的每次迭代过程中,每个粒子的位置变量 X i X_i Xi? 和速度变量 V i V_i Vi?通过以下公式进行更新:
V i ( t + 1 ) = ω V i ( t ) + c 1 R 1 ( t ) ( p b e s t i ( t ) ? X i ( t ) ) + c 2 R 2 ( t ) ( g b e s t ( t ) ? X i ( t ) ) X i ( t + 1 ) = X i ( t ) + V i ( t + 1 ) \begin{gathered}V_i\left(t+1\right)=\omega V_i\left(t\right)+c_1R_1\left(t\right)(pbest_i\left(t\right)-X_i\left(t\right))+c_2R_2\left(t\right)(gbest(t)-X_i\left(t\right))\\\\\\X_i\left(t+1\right)=X_i\left(t\right)+V_i\left(t+1\right)\end{gathered} Vi?(t+1)=ωVi?(t)+c1?R1?(t)(pbesti?(t)?Xi?(t))+c2?R2?(t)(gbest(t)?Xi?(t))Xi?(t+1)=Xi?(t)+Vi?(t+1)?
其中 t t t是当前迭代数, ω \omega ω是惯性权重, c 1 c_1 c1?和 c 2 c_2 c2?是加速度系数, R 1 ( t ) R_1(t) R1?(t)和 R 2 ( t ) R_2\left(t\right) R2?(t)是两个向量,向量中每个元索取值范围为 [ 0 , 1 ] n [0,1]^n [0,1]n, p b e s t i ( t ) pbest_i(t) pbesti?(t) 是第 i i i个粒子的历史最优解, g b e s t ( t ) gbest(t) gbest(t)是所有粒子的历史最优解。 c 1 R 1 ( t ) ( p b e s t i ( t ) ? X i ( t ) ) c_1R_1(t)(pbest_i(t)-X_i(t)) c1?R1?(t)(pbesti?(t)?Xi?(t))为认知部分, c 2 R 2 ( t ) ( g b e s t ( t ) ? X i ( t ) ) c_2R_2(t)(gbest(t)-X_i(t)) c2?R2?(t)(gbest(t)?Xi?(t))为社会部分。
当优化问题存在大量局部最优值和具有高维特点时,传统PSO算法在处理此类问题时会过早收敛,从而导致其优化效果不佳。首先来看 g b e s t gbest gbest 对算法收敛过程的影响,将上述公式进行变换,可得:
V i ( t + 1 ) = ω V i ( t ) + θ 1 ( p 1 ? X i ( t ) ) \left.V_i\left(t+1\right)=\omega V_i\left(t\right)+\theta_1\left(p_1\right.-X_i\left(t\right)\right) Vi?(t+1)=ωVi?(t)+θ1?(p1??Xi?(t))
其中,
θ 1 ? = c 1 ? R 1 ( t ) + c 2 ? R 2 ( t ) \theta_1\:=c_1\:R_1\left(t\right)+c_2\:R_2\left(t\right) θ1?=c1?R1?(t)+c2?R2?(t)
p 1 ? = ? c 1 R 1 ( t ) c 1 R 1 ( t ) + c 2 R 2 ( t ) p b e s t i ( t ) + c 2 R 2 ( t ) c 1 R 1 ( t ) + c 2 R 2 ( t ) g b e s t ( t ) p_{1}\:=\:\frac{c_{1}R_{1}\left(t\right)}{c_{1}R_{1}\left(t\right)+c_{2}R_{2}\left(t\right)}pbest_{i}\left(t\right)+\frac{c_{2}R_{2}\left(t\right)}{c_{1}R_{1}\left(t\right)+c_{2}R_{2}\left(t\right)}gbest(t) p1?=c1?R1?(t)+c2?R2?(t)c1?R1?(t)?pbesti?(t)+c1?R1?(t)+c2?R2?(t)c2?R2?(t)?gbest(t)
p 1 p_1 p1?和 X i X_i Xi?的差决定了粒子群的种群多样性,而 p b e s t i pbest_i pbesti? 和 g b e s t gbest gbest的取值多样性决定了 p 1 p_1 p1?取值的多样性。由于 g b e s t gbest gbest的影响,随着送代过程的继续,粒子逐渐向 g b e s t gbest gbest靠拢,这导致 p b e s t i pbest_i pbesti?逐渐接近 g b e s t gbest gbest,进而导致粒子群的种群多样性大幅降低。 p 1 p_1 p1?在很大程度上决定着传统PSO 算法在搜索过程中的勘探能力和开采能力。
为了解决传统PSO算法的过早收敛问题,本文提出了CSO算法。该算法去掉了
p
b
e
s
t
i
pbest_i
pbesti?和
g
b
e
s
t
gbest
gbest两个变量,引入了粒子间的成对竞争机 制。在该机制中,竞争失败的粒子将向竞争胜利的粒子学习,而不是向
p
b
e
s
t
i
pbest_i
pbesti?和
g
b
e
s
t
gbest
gbest学习,这将较好地解决传统PSO算法的过早收敛问
题。
基本理论
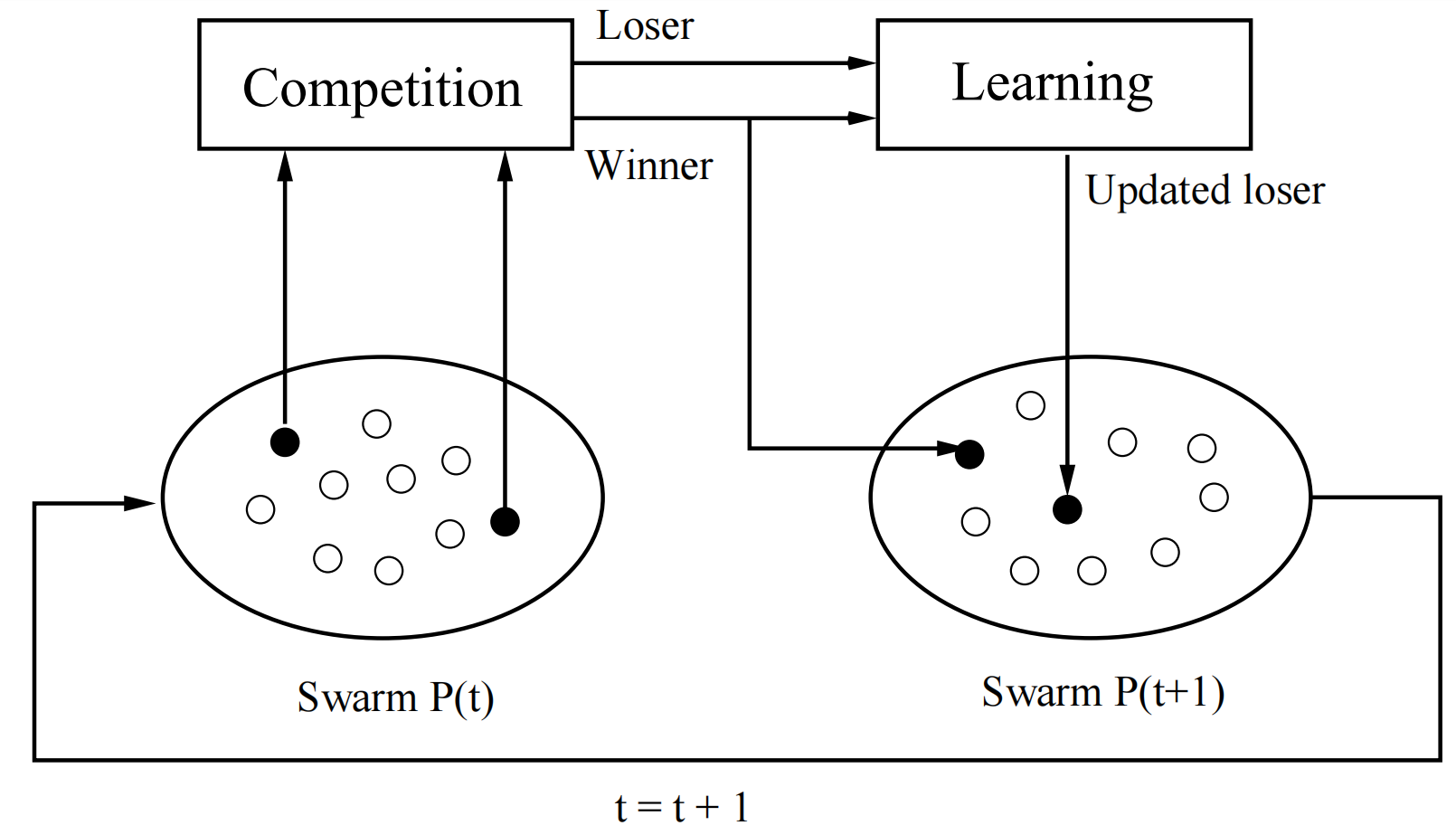
CSO 算法的总体思想如图所示。在每一次迭代过程中,随机从粒子群 P ( t ) P(t) P(t)中选择一对粒子进行竞争。竞争成功的粒子直接进入下一次迭代,竞争失败的粒子将向竞争成功的粒子学习并更新自己的位置变量和速度变量。该操作完成后,将这一对粒子从粒子群 P ( t ) P(t) P(t)中剔除, 将竞争成功的粒子和更新后的失败粒子加入到粒子群 P ( t + 1 ) P(t+1) P(t+1)中。当所有粒子从粒子群 P ( t ) P(t) P(t)中移到粒子群 P ( t + 1 ) P(t+1) P(t+1)中后,算法进入下一次迭代。根据上图可知,每一次迭代将会使粒子群 P P P中一半的粒子得到更新。
竞争失败的粒子的速度变量和位置变量更新如以下公式所示:
V l , k ( t + 1 ) = R 1 ( k , t ) V l , k ( t ) + R 2 ( k , t ) ( X w , k ( t ) ? X l , k ( t ) ) + φ R 3 ( k , t ) ( X ˉ k ( t ) ? X l , k ( t ) ) \begin{aligned}V_{l,k}\left(t+1\right)&=R_1\left(k,t\right)V_{l,k}\left(t\right)+R_2\left(k,t\right)(X_{w,k}\left(t\right)-X_{l,k}\left(t\right))+\varphi R_3\left(k,t\right)(\bar{X}_k\left(t\right)-X_{l,k}\left(t\right))\end{aligned} Vl,k?(t+1)?=R1?(k,t)Vl,k?(t)+R2?(k,t)(Xw,k?(t)?Xl,k?(t))+φR3?(k,t)(Xˉk?(t)?Xl,k?(t))?
X l , k ( t + 1 ) = X l , k ( t ) + V l , k ( t + 1 ) \begin{aligned}X_{l,k}\left(t+1\right)&=X_{l,k}\left(t\right)+V_{l,k}\left(t+1\right)\end{aligned} Xl,k?(t+1)?=Xl,k?(t)+Vl,k?(t+1)?
其中, X w , k ( t ) X_{w,k}(t) Xw,k?(t)表示第 t t t代的第 k k k轮竞争中竞争成功粒子的位置, X l , k ( t ) X_{l,k}(t) Xl,k?(t)表示第 t t t代的第 k k k轮竞争中竞争失败粒子的位置, V l , k ( t ) V_{l,k}(t) Vl,k?(t)表示第 t t t 代的第 k k k轮竞争中竞争失败粒子的速度, R 1 ( k , t ) R_1(k,t) R1?(k,t)、 R 2 ( k , t ) R_2(k,t) R2?(k,t)、 R 3 ( k , t ) ∈ [ 0 , 1 ] R_3(k,t)\in[0,1] R3?(k,t)∈[0,1]分别表示算法第 t t t次迭代的第 k k k轮竞争中随机生成的向量。
X ˉ k ( t ) \bar{X}_k\left(t\right) Xˉk?(t)表示第 t t t代的第 k k k轮竞争中相关粒子的位置平均值,它分为全局版本和局部版本。
- X ˉ k g ( t ) \bar{X}_k^g(t) Xˉkg?(t)表示 P ( t ) P(t) P(t)中所有粒子的位置平均值,是全局版本。
- X ˉ l , k l ( t ) \bar{X}_{l,k}^l(t) Xˉl,kl?(t)表示在竞争失败粒子的预定义邻域内所有粒子的位置平均值,是局部版本。领域控制可以增加粒子群的种群多样性,这可能会提高CSO算法的搜索能力。
算法流程

1.3 勘探能力与开采能力分析
粒子群优化算法 PSO 是一种模拟自然界生物群体行为的随机搜索算法,它通过调整粒子的速度和位置来寻找最优解。在这个过程中,粒子需要平衡两种能力:
- 勘探能力(Exploration Ability):指粒子在搜索空间中探索新区域的能力,也就是全局寻优能力。勘探能力越强,粒子越容易跳出局部最优解,找到更好的解。
- 开采能力(Exploitation Ability):指粒子在搜索空间中开发已知区域的能力,也就是局部寻优能力。开采能力越强,粒子越容易收敛到最优解,提高搜索精度。
粒子群优化算法 PSO 的参数设置和拓扑结构都会影响粒子的勘探能力和开采能力,因此需要根据不同的优化问题进行合理的调整。一般来说,算法在前期需要较强的勘探能力,而在后期需要较强的开采能力,以达到最佳的性能。

首先分析一下CSO算法的勘探能力,将上述公式转换:
V
i
(
t
+
1
)
=
R
1
(
k
,
t
)
V
i
(
t
)
+
θ
2
(
p
2
?
X
i
(
t
)
)
\begin{aligned} &\left.V_i\left(t+1\right)=R_1\left(k,t\right)V_i\left(t\right)+\theta_2\left(p_2\right.-X_i\left(t\right)\right) \\ \end{aligned}
?Vi?(t+1)=R1?(k,t)Vi?(t)+θ2?(p2??Xi?(t))?
θ 2 = R 2 ( k , t ) + φ R 3 ( k , t ) \theta_{2} =R_2\left(k,t\right)+\varphi R_3\left(k,t\right) θ2?=R2?(k,t)+φR3?(k,t)
p 2 = R 2 ( k , t ) R 2 ( k , t ) + φ R 3 ( k , t ) X w ( t ) + φ R 3 ( k , t ) R 2 ( t ) + φ R 3 ( k , t ) X ˉ ( t ) p_{2} =\frac{R_2\left(k,t\right)}{R_2\left(k,t\right)+\varphi R_3\left(k,t\right)}X_w\left(t\right)+\frac{\varphi R_3\left(k,t\right)}{R_2\left(t\right)+\varphi R_3\left(k,t\right)}\bar{X}\left(t\right) p2?=R2?(k,t)+φR3?(k,t)R2?(k,t)?Xw?(t)+R2?(t)+φR3?(k,t)φR3?(k,t)?Xˉ(t)
CSO算法的种群多样性是高于传统PSO算法的,因为 X w ( t ) X_w(t) Xw?(t)和 X ˉ ( t ) \bar{X}(t) Xˉ(t)的取值更加地多样。下面展示CSO算法的勘探能力是如何高于传统PSO算法的。
首先看图 2, g b e s t ( t ) gbest(t) gbest(t)陷入了局部最优,在传统PSO算法中,两个被选择的粒子均会向 g b e s t ( t ) gbest(t) gbest(t)靠近,这最终使得算法陷入局部最优的陷阱,导致算法优化结果的不佳。现在去掉向 g b e s t ( t ) gbest(t) gbest(t)更新的方式,所有粒子均只向各自的 p b e s t ( t ) pbest(t) pbest(t)更新,如图 3。从图可以看出,被选择的粒子会跳出局部最优的陷阱,使得算法的勘探能力得到了提升。但是如果 p b e s t ( t ) pbest(t) pbest(t)也陷入了局部最优,如图 4,算法也会陷入局部最优的陷阱,导致算法的勘探能力下降。因此,去掉向 g b e s t ( t ) gbest(t) gbest(t) 与 p b e s t ( t ) pbest(t) pbest(t) 更新的方式,粒子的更新采用成对粒子竞争更新机制,传统PSO算法也就演变为CSO算法。如图 4,由于所有粒子分布在样本空间的不同位置,粒子的更新就变得更加多样化,非常有助于算法脱离局部最优的陷阱,从而使得算法的勘探能力大幅提升。
然后分析一下CSO算法的开采能力。CSO算法的开采阶段是在勘探阶段之后,是在勘探阶段基础上继续小规模地提高算法的优化结果。在传统的PSO算法中,有以下关系:
{ f ( g b e s t ( t ) ) ≤ f ( p b e s t w ( t ) ) ≤ f ( X w ( t ) ) f ( g b e s t ( t ) ) ≤ f ( b e s t l ( t ) ) ≤ f ( X l ( t ) ) \left.\left\{\begin{array}{c}f(gbest(t))\leq f\left(pbest_w\left(t\right)\right)\leq f\left(X_w\left(t\right)\right)\\f(gbest(t))\leq f\left(best_l\left(t\right)\right)\leq f\left(X_l\left(t\right)\right)\end{array}\right.\right. {f(gbest(t))≤f(pbestw?(t))≤f(Xw?(t))f(gbest(t))≤f(bestl?(t))≤f(Xl?(t))?
随着迭代过程的继续,t 越来越大,有:
{ p b e s t w ( t ) ≈ g b e s t ( t ) p b e s t l ( t ) ≈ g b e s t ( t ) \left.\left\{\begin{array}{l}pbest_w\left(t\right)\approx gbest(t)\\pbest_l\left(t\right)\approx gbest(t)\end{array}\right.\right. {pbestw?(t)≈gbest(t)pbestl?(t)≈gbest(t)?
然后令:

其中
p
1
′
p_1^{\prime}
p1′?是
p
1
p_1
p1?的数学期望,
p
2
′
p_2^{\prime}
p2′?是
p
2
p_2
p2?在
φ
=
0
\varphi=0
φ=0的数学期望。可以得到:
Δ
F
2
(
t
)
≤
Δ
F
1
(
t
)
\Delta F_2\left(t\right)\leq\Delta F_1\left(t\right)
ΔF2?(t)≤ΔF1?(t)
与传统PSO算法相比,CSO算法有更好的能力开发与最优粒子相接近的粒子,也就是其开发能力更好,即局部搜索能力更强。此证明过程主要与其勘探过程结合来看。
References
Cheng R, Jin Y. A competitive swarm optimizer for large scale optimization[J]. IEEE transactions on cybernetics, 2014, 45(2): 191-204.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 汽车电子行业的 C 语言编程标准
- SpringBoot启动打印banner:佛祖保佑-永不宕机-永无BUG
- 笔记本电脑和电脑上的 7 款最佳免费且易于使用的 PDF 编辑软件
- Java毕业设计-基于jsp+servlet的家用电器购物商城管理系统-第87期
- 2023年大模型回顾
- DGL离线安装
- 线程池介绍
- mkdir命令
- Python学习从0到1 day4 python格式化输出和输入方法
- Golang,Gin框架使用ShouldBindJSON时出现EOF报错