代码随想录算法训练营Day17|110.平衡二叉树、257. 二叉树的所有路径、 404.左叶子之和
发布时间:2024年01月12日
一、110.平衡二叉树
题目描述: 给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
1.递归法
- 明确递归函数的参数和返回值
参数:当前传入节点。
返回值:以当前传入节点为根节点的树的高度。- 明确终止条件
递归的过程中依然是遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0- 明确单层递归的逻辑
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则则返回-1,表示已经不是二叉平衡树了。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
private int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = getHeight(root.left);
if(leftHeight == -1) {
return -1;
}
int rightHeight = getHeight(root.right);
if (rightHeight == -1) {
return -1;
}
// 左右子树高度差>1,return -1表示已经不是平衡树了
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
return Math.max(leftHeight, rightHeight) + 1;
}
}
二、257. 二叉树的所有路径
题目描述: 给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
1. 递归法
- 递归函数函数参数以及返回值
要传入根节点,记录每一条路径的path,和存放结果集的result。- 确定递归终止条件
- 确定单层递归逻辑
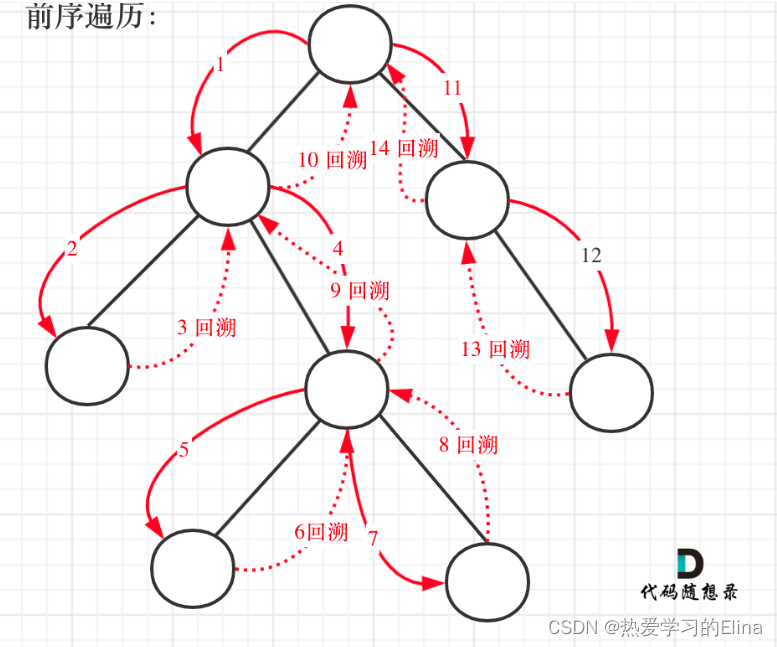
因为是前序遍历,需要先处理中间节点,中间节点就是我们要记录路径上的节点,先放进path中。然后是递归和回溯的过程,上面说过没有判断cur是否为空,那么在这里递归的时候,如果为空就不进行下一层递归了。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<>();
if (root == null) {
return res;
}
List<Integer> paths = new ArrayList<>();
traversal(root, paths, res);
return res;
}
private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
paths.add(root.val);
// 叶子结点
if (root.left == null && root.right == null) {
// 输出
StringBuilder sb = new StringBuilder();
for (int i = 0; i < paths.size() - 1; i++) {
sb.append(paths.get(i)).append("->");
}
sb.append(paths.get(paths.size() - 1));
res.add(sb.toString());
return;
}
if (root.left != null) {
traversal(root.left, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
if (root.right != null) {
traversal(root.right, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
}
}
三、 404.左叶子之和
题目描述: 计算给定二叉树的所有左叶子之和。
1.迭代法
- 确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int。- 确定终止条件
如果遍历到空节点,那么左叶子值一定是0。
注意,只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0。- 确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
int leftValue = sumOfLeftLeaves(root.left); // 左
int rightValue = sumOfLeftLeaves(root.right); // 右
int midValue = 0;
if (root.left != null && root.left.left == null && root.left.right == null) {
midValue = root.left.val;
}
int sum = midValue + leftValue + rightValue; // 中
return sum;
}
}
文章来源:https://blog.csdn.net/qq_41929830/article/details/135547473
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 研讨会分享 | 非遗文化的守正创新与数字化传播
- php 源码解读函数解释
- mipi dsi协议DBI/DPI接口
- 第六回 花和尚倒拔垂杨柳 豹子头误入白虎堂-安装服务器管理面板AMH和cyberpanel
- netstat命令使用
- 技术人员想转管理学习PMP证书有用吗?
- 13.3 Start a sequence
- 第十六章 : Spring Boot JWT 集成redis实现分布式token
- 项目经理和产品经理的区别,如何判断自己适合哪个,从事该岗位前期需做的准备(学习技能考、哪些证书)?
- vue实现在一个方法执行完后执行另一个方法