day17 二叉树part04

110. 平衡二叉树

简单
给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return (getHeight(root) == -1) ? false : true; 
    }

    public int getHeight(TreeNode node){
        //遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0
        if (node == null) {
            return 0;
        } 

        // 如果左右子树返回了-1 说明已经有子树不是平衡二叉树了，继续返回-1
        int leftHeight = getHeight(node.left);
        if (leftHeight == -1) return -1;
        int rightHeight = getHeight(node.right);
        if (rightHeight == -1) return -1;

        // 左右子树高度差大于1，return -1表示已经不是平衡树了
        int diff = Math.abs(leftHeight - rightHeight)
        if (diff > 1) return -1;

        // 由子节点的高度计算当前节点的高度
        int height = Math.max(leftHeight, rightHeight) + 1;
        return height;

    }
}

257. 二叉树的所有路径

简单
给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。

难点1：要想顺序记录从根节点到叶子节点的路径，就需要从上到下访问，所以这个题只能用前序遍历。

难点2：第一次遇到回溯的题目，要懂得回溯的原理和思想。

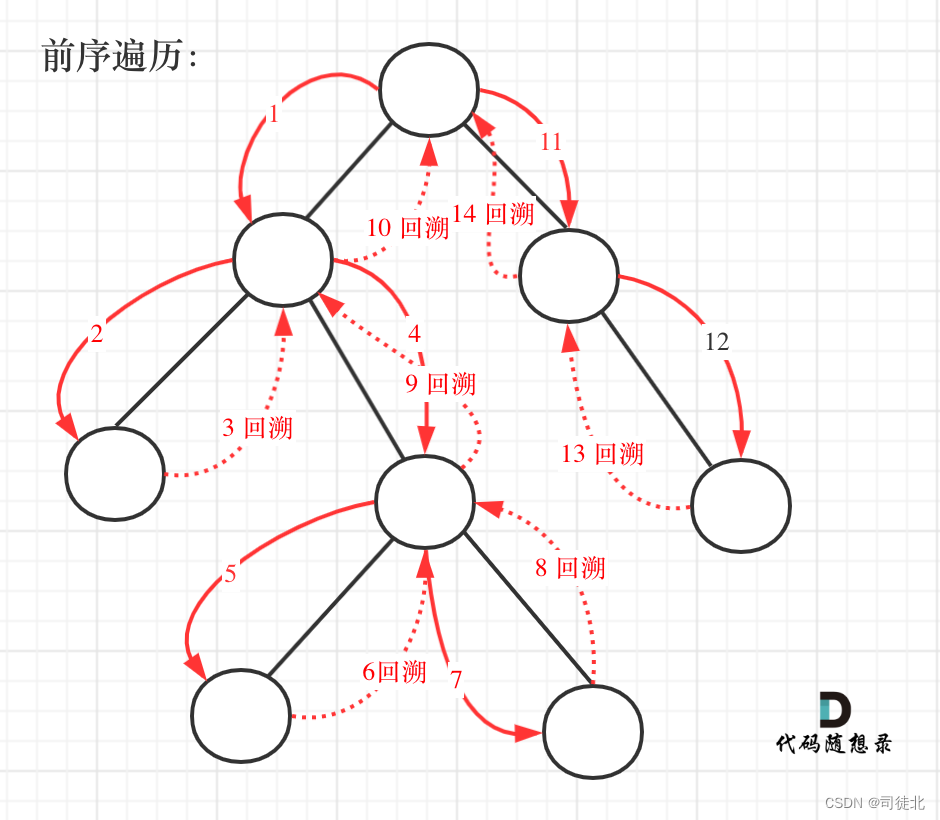
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>(); // 存放最终结果
        if (root == null) {
            return res;
        }
        List<Integer> path = new ArrayList<>(); // 存放最终结果中的单独一条路径
        traversal(root, path, res);

        return res;
    }
    public void traversal(TreeNode node, List<Integer> path, List<String> res) {
        path.add(node.val); //前序遍历，先加入中间节点
        if (node.left == null && node.right == null) { // 如果当前这个节点就是一个叶子节点，就把当前这条路径加入res中
            StringBuilder sb = new StringBuilder(); //StringBuilder拼接更方便
            for (int i = 0; i < path.size() - 1; i++) {
                sb.append(path.get(i)); // 这里不是sb.add，是append
                sb.append("->");
            }
            sb.append(path.get(path.size() - 1)); //最后一个节点后面没有"->"，所以单独处理
            res.add(sb.toString()); //收集这个路径
            return; //到这个节点就停了，后面不需要处理了，可以退出了，这里没有删除当前path的最后一个节点值的原因是，当前函数结束后，会在它的上个递归里删除
        }
        // 递归和回溯是同时进行，所以要放在同一个花括号里
        if (node.left != null) { //如果左节点不为空，把左节点送去继续递归
            traversal(node.left, path, res);
            path.remove(path.size() - 1); //！！！回溯，这一步是最难理解的，这一句代表着，把path中的路径再回退一步,回退这一步永远是站在当前节点，去取回当前节点的左或右节点，就好像往筒里放乒乓球，放进去了要拿出来
        }
        if (node.right != null) {
            traversal(node.right, path, res);
            path.remove(path.size() - 1);
        }
    }
}

其实不用回溯也能做（或许是回溯了，但是回溯得不明显，递归一定伴随着回溯）（回溯可以理解为从某一节点出发然后又回到该节点），来看下力扣精选的题解代码：

// 每个节点访问的时候先把他存储起来，到叶子结点的时候再添加到集合中，最后返回集合的值
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        dfs(root, "", res);
        return res;
    }

    private void dfs(TreeNode root, String path, List<String> res) {
        //如果为空，直接返回
        if (root == null)
            return;
        //如果是叶子节点，说明找到了一条路径，把它加入到res中
        if (root.left == null && root.right == null) {
            res.add(path + root.val);
            return;
        }
        //如果不是叶子节点，在分别遍历他的左右子节点
        dfs(root.left, path + root.val + "->", res);
        dfs(root.right, path + root.val + "->", res);
    }

作者：数据结构和算法
链接：https://leetcode.cn/problems/binary-tree-paths/solutions/400434/257-er-cha-shu-de-suo-you-lu-jing-tu-wen-jie-xi-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

404. 左叶子之和

简单
给定二叉树的根节点 root ，返回所有左叶子之和。

难点：左叶子之和一定是等于左子树的左叶子之和加上右子树的左叶子之和的。这是这里能用递归的根本逻辑。

递归：当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。
层次：这个题层次遍历法也能做，因为层次遍历能访问到所有的节点，对所有的节点都判断一次: if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) 然后加上值就行，也不复杂。
这里我们写一下递归法：
建议多默写几遍这个题的递归法，我觉得有好处

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return postOrder(root);
    }
    public int postOrder(TreeNode node) {
        if (node == null) {
            return 0;
        }
        
        int sumLeft;
        int sumRight;

        // 如果当前节点的左节点就是一个叶子节点，那么记录下它的值
        if (node.left != null && node.left.left == null && node.left.right == null) {
            sumLeft = node.left.val;
        } else {
            // 如果当前节点的左节点不是一个叶子节点(要么是空节点，要么下面还有很多节点)，那么就继续递归
            sumLeft = postOrder(node.left);
        }
        
        // 右节点也放入递归计算它的左叶子
        sumRight = postOrder(node.right);

        return sumLeft + sumRight;
    }
}