JAVA算法介绍(二)
?6?归并排序算法
归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列
分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
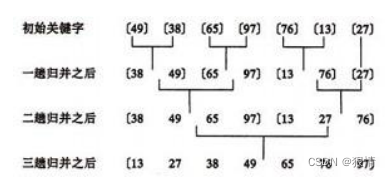
public class MergeSortTest {
public static void main(String[] args) {
int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
print(data);
mergeSort(data);
System.out.println("排序后的数组:");
print(data);
}
public static void mergeSort(int[] data) {
sort(data, 0, data.length - 1);
}
public static void sort(int[] data, int left, int right) {
if (left >= right)
return;
// 找出中间索引
int center = (left + right) / 2;
// 对左边数组进行递归
sort(data, left, center);
// 对右边数组进行递归
sort(data, center + 1, right);
// 合并
merge(data, left, center, right);
print(data);
}
/**
* 将两个数组进行归并,归并前面 2 个数组已有序,归并后依然有序
*
* @param data
* 数组对象
* @param left
* 左数组的第一个元素的索引
* @param center
* 左数组的最后一个元素的索引,center+1 是右数组第一个元素的索引
* @param right
* 右数组最后一个元素的索引
*/
public static void merge(int[] data, int left, int center, int right) {
// 临时数组
int[] tmpArr = new int[data.length];
// 右数组第一个元素索引
int mid = center + 1;
// third 记录临时数组的索引
int third = left;
// 缓存左数组第一个元素的索引
int tmp = left;
while (left <= center && mid <= right) {
// 从两个数组中取出最小的放入临时数组
if (data[left] <= data[mid]) {
tmpArr[third++] = data[left++];
} else {
tmpArr[third++] = data[mid++];
}
}
// 剩余部分依次放入临时数组(实际上两个 while 只会执行其中一个)
while (mid <= right) {
tmpArr[third++] = data[mid++];
}
while (left <= center) {
tmpArr[third++] = data[left++];
}
// 将临时数组中的内容拷贝回原数组中
// (原 left-right 范围的内容被复制回原数组)
while (tmp <= right) {
data[tmp] = tmpArr[tmp++];
}
}
public static void print(int[] data) {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + "\t");
}
System.out.println();
}
}
7?桶排序算法
?
public static void bucketSort(int[] arr){int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int i = 0; i < arr.length; i++){max = Math.max(max, arr[i]);min = Math.min(min, arr[i]);}//创建桶int bucketNum = (max - min) / arr.length + 1;ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());}//将每个元素放入桶for(int i = 0; i < arr.length; i++){int num = (arr[i] - min) / (arr.length);bucketArr.get(num).add(arr[i]);}//对每个桶进行排序for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));}}
8?基数排序算法?
?
public class radixSort {inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,101,56,17,18,23,34,15,35,25,53,51};public radixSort(){sort(a);for(inti=0;i<a.length;i++){System.out.println(a[i]);}}public void sort(int[] array){//首先确定排序的趟数;int max=array[0];for(inti=1;i<array.length;i++){if(array[i]>max){max=array[i];}}int time=0;//判断位数;while(max>0){max/=10;time++;}//建立 10 个队列;List<ArrayList> queue=newArrayList<ArrayList>();for(int i=0;i<10;i++){ArrayList<Integer>queue1=new ArrayList<Integer>();queue.add(queue1);}//进行 time 次分配和收集;for(int i=0;i<time;i++){//分配数组元素;for(intj=0;j<array.length;j++){//得到数字的第 time+1 位数;int x=array[j]%(int)Math.pow(10,i+1)/(int)Math.pow(10, i);ArrayList<Integer>queue2=queue.get(x);queue2.add(array[j]);queue.set(x, queue2);}int count=0;//元素计数器;//收集队列元素;for(int k=0;k<10;k++){while(queue.get(k).size()>0){ArrayList<Integer>queue3=queue.get(k);array[count]=queue3.get(0);queue3.remove(0);count++;}}}}}
9?剪枝算法
?
10?回溯算法
11?最短路径算法
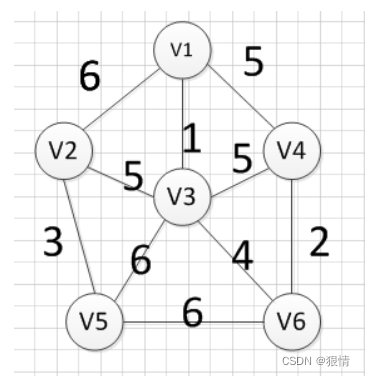
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 软件报错msvcp120.dll丢失怎么办?总共有6个msvcp120.dll丢失的解决方法分享
- 浅谈数字孪生的应用与发展
- 学会这个技巧,制作电子杂志SOEASY
- 你可能不知道的5款好用封面设计工具,快来一探究竟吧!
- 爬虫中HTTP请求库和requests详解
- winfrom 获取dataGridView1选中行数据
- “华为杯“第四届中国研究生数学建模竞赛-D题:邮路规划与邮车调度
- 数据库中修改表的语句
- 百度UEditor插入图片尺寸自动适应编辑框大小问题
- jsES6+新语法