Trie字符串统计

题目传送门：835.Trie字符串统计

维护一个字符串集合，支持两种操作：

1. I x?向集合中插入一个字符串?x；
2. Q x?询问一个字符串在集合中出现了多少次。

共有?N?个操作，所有输入的字符串总长度不超过?105105，字符串仅包含小写英文字母。

输入格式

第一行包含整数?N，表示操作数。

接下来?N?行，每行包含一个操作指令，指令为?I x?或?Q x?中的一种。

输出格式

对于每个询问指令?Q x，都要输出一个整数作为结果，表示?x?在集合中出现的次数。

每个结果占一行。

数据范围

1≤N≤2?1e4

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

试题解析

算法分析

本题使用Trie树的方法。
Trie树又称字典树、单词查找树。是一种能够高效存储和查找字符串集合的数据结构。

Trie树的每一个节点都有对应的字符指针，我们可以根据这个性质来进行字符串的插入

试题解析

本题插入的字符串都为小写字母，所以每一个字符的下一个元素都为小写字母，只需要申请26个空间即可存储。
我们可以通过一个二维数组son来记录每一步的插入操作，son[p][u]的p为当前节点，u为下一个节点的字母，每一个字母插入后都进行存储，最后再进行字符串结尾的标记和计数，便可得到最终结果。

模拟Trie树操作如下：

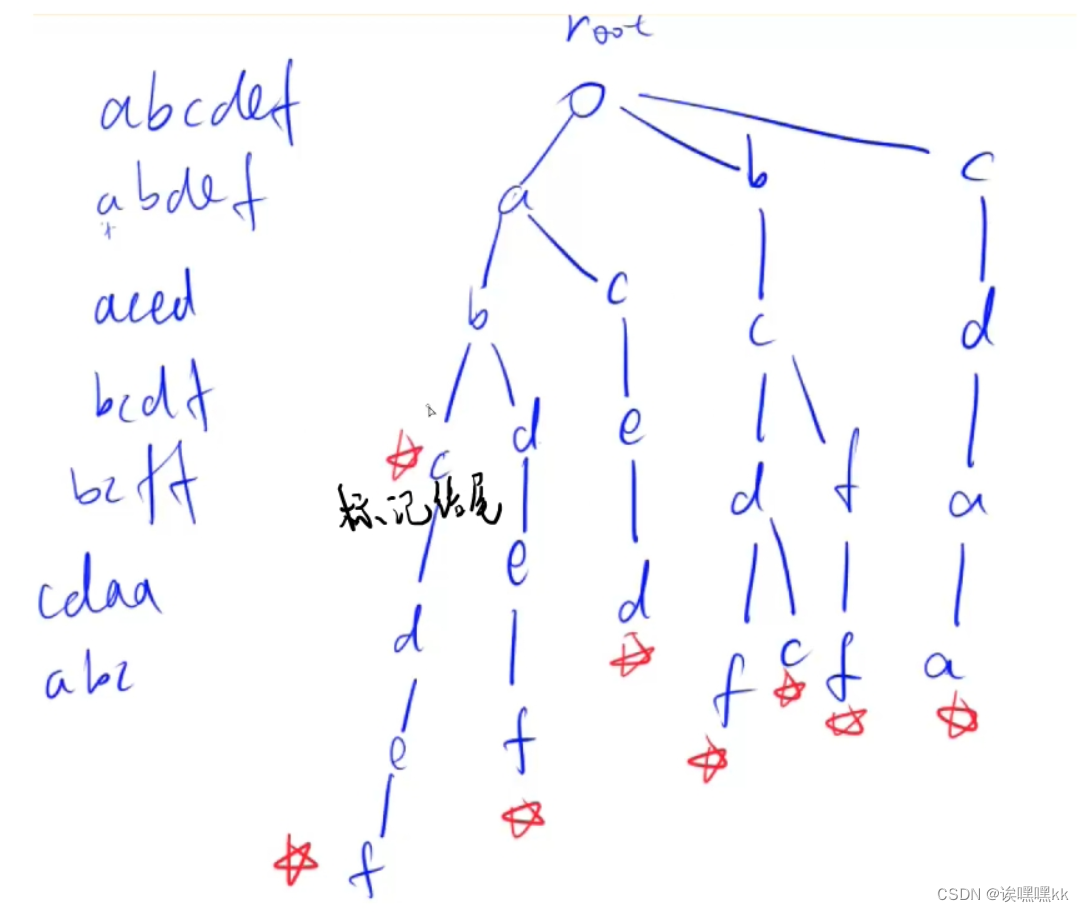
操作过程

初始化：

• son[][]存储子节点的位置，分支最多26条
• cnt[]存储以某节点结尾的字符串个数并起标记作用
• idx表示当前要插入的节点是第几个,每创建一个节点值+1

插入操作：

p为当前节点，u为下一个字母对应的二维数组的位置，每一次新字母插入时，都给其赋值为++idx，即是下一个元素。
然后更新p的值，直到字符串遍历完成，cnt为字符串结束标志，并能起计数作用。

void insert(char str[]) {
	int p = 0;  //类似指针，指向当前节点
	for (int i = 0; str[i]; i++) {
		int u = str[i] - 'a'; //将字母转化成数字
		if (!son[p][u]) son[p][u] = ++idx;
		//若该节点不存在，创建节点，值为下一个位置
		p = son[p][u]; //使p指向下一个节点
	}
	cnt[p]++; //结束时建立标志
}

查询操作：

与插入操作类似，注意若当前字母不存在时，则字符串一定不存在，查询失败

int query(char str[]) {
	int p = 0;
	for (int i = 0; str[i]; i++) {
		int u = str[i] - 'a';
		if (!son[p][u]) return 0; //该节点不存在即字符串不存在
		p = son[p][u];
	}
	return cnt[p]; //返回字符串出现次数
}

完整代码

#include<iostream>
using namespace std;

const int N = 100010;
//son[][]存储子节点的位置，分支最多26条
//cnt[]存储以某节点结尾的字符串个数并起标记作用
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][26], cnt[N], idx;
char str[N];
void insert(char str[]) {
	int p = 0;  //类似指针，指向当前节点
	for (int i = 0; str[i]; i++) {
		int u = str[i] - 'a'; //将字母转化成数字
		if (!son[p][u]) son[p][u] = ++idx;
		//若该节点不存在，创建节点，值为下一个位置
		p = son[p][u]; //使p指向下一个节点
	}
	cnt[p]++; //结束时建立标志
}
int query(char str[]) {
	int p = 0;
	for (int i = 0; str[i]; i++) {
		int u = str[i] - 'a';
		if (!son[p][u]) return 0; //该节点不存在即字符串不存在
		p = son[p][u];
	}
	return cnt[p]; //返回字符串出现次数
}

int main() {
	int n;
	scanf("%d", &n);

	while (n--) {
		char op[2];
		scanf("%s%s", op, str);
		if (op[0] == 'I') insert(str);
		else printf("%d\n", query(str));
	}
	return 0;
}