P2437 蜜蜂路线---一只小蜜蜂啊，飞入花丛中啊......

# 蜜蜂路线

## 题目背景

无

## 题目描述

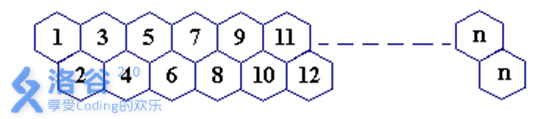
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房 $m$ 开始爬到蜂房 $n$，$m<n$，有多少种爬行路线？（备注：题面有误，右上角应为 $n-1$）


## 输入格式

输入 $m,n$ 的值

## 输出格式

爬行有多少种路线

## 样例 #1

### 样例输入 #1

```
1 14
```

### 样例输出 #1

```
377
```

## 提示

对于100%的数据，$1 \le M,N\le 1000$

? ? ? ?不知道各位小伙伴看到这题时，会怎么操作呢？其实仔细一想就是斐波那契数列与高精度加法的结合应用，如果这两个知识点不会的小伙伴，那可以看一下本蒟蒻前面的相关文章。

? ?我们现在开始讲述本题的重点，就是如何把斐波那契数列与高精度算法结合起来呢？毫无疑问的是要用到数组。我们运用数组就可以把二者有机结合起来了。各位小伙伴可以尝试一下，看能不能写出题解。

? ? ?当我也是按照这种思维思考时，便遇到了一个问题就是如何计算数组的实际长度，经过我七七四十九分钟的思考，终于想到怎么计算了，一般我们计算一个数组的长度会从头开始，但这样做这题显然不行，那么我们就反着来，从最后开始，只要其元素项为0，那就减一就OK了，这样这道题就算解出来了，直接代码吧.

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int Max(int a,int b) {
	if (a > b){
		return a;
	}
	else return b;
}
int main() {
	int n, m, arr[1005]={1}, brr[1005] = {1}, a, b, c;
	scanf("%d%d", &m, &n);
	n = n-m;
	m = 1;
	if (n == 1) {
		printf("1");
	}
	else {
		
		while (m < n) {
			int crr[1005] ={0};
			a = 1004;
			b = 1004;
				while (arr[a] == 0) {
					a--;
			}
			while (brr[b] == 0) {
				b--;
			}
			c = Max(a,b) + 1;
			for (int i = 0;i <= c;i++) {
				crr[i]+= arr[i] + brr[i];
				crr[i + 1] = crr[i] / 10;
				crr[i] = crr[i] % 10;
			}
			for (int i = 0;i <= a;i++){
				brr[i] = arr[i];
			}
			for (int i = 0;i <=c;i++){
				arr[i] = crr[i];
			}
			m++;
		}
	}

	for (int i = c - 1;i >= 0;i--) {
		printf("%d", arr[i]);
	}

	return 0;
}

不知道各位看到这题时，各位是这样思考的嘛，应该还有另外的思想，动动脑筋，加油·！