模式识别与机器学习-无监督学习-聚类

谨以此博客作为复习期间的记录

监督学习&无监督学习

监督学习和无监督学习是机器学习中两种基本的学习范式。

1. 监督学习：

   • 定义：监督学习是一种机器学习范式，在这种范式中，模型通过已标记的训练数据进行训练，每个训练样本都有一个标签或目标值。
   • 特点：模型在学习过程中使用输入数据与其对应的已知输出（标签或目标值）之间的关系，目的是学习从输入到输出的映射关系，以便对新的未知数据做出准确的预测或分类。
   • 优点：
     • 可以利用已知的标签信息来进行精确的预测或分类。
     • 在训练过程中可以评估模型的性能，并进行调整和改进。
     • 适用于大多数真实世界的问题，如图像识别、语音识别、自然语言处理等。
   • 缺点：
     • 需要大量标记好的训练数据，数据标记成本高。
     • 对于某些问题，标签数据可能不容易获得或标记。

2. 无监督学习：

   • 定义：无监督学习是一种机器学习方法，其中模型根据未标记的数据进行学习，没有对应的目标输出。
   • 特点：在无监督学习中，模型试图从数据中发现隐藏的模式、结构或特征，而不需要预先定义的输出标签。
   • 优点：
     • 可以发现数据中的潜在结构、关联和规律，有助于理解数据本身。
     • 适用于数据探索和降维等任务。
     • 不需要标签，因此不受标签获取成本的影响。
   • 缺点：
     • 对于一些任务，无法直接量化或验证模型学到的信息。
     • 在训练过程中难以衡量模型的性能。

K-means

K-means聚类的优点：

1. 简单快速：K-means是一种直观且易于实现的聚类算法，计算效率高，适用于大规模数据集。
2. 可扩展性：对于大规模数据，K-means算法具有良好的可扩展性和高效性。
3. 对高斯分布接近的簇效果较好：当簇近似服从高斯分布时，K-means算法的聚类效果较好。

K-means的局限性：

1. 硬划分数据：K-means对数据点进行硬划分，即每个数据点只能属于一个簇，当数据存在噪声或异常值时，可能会导致点被错误分配到不合适的簇中。
2. 对簇形状和大小的假设：K-means假设簇是球形的，并且每个簇的概率相等，这在某些场景下可能不符合实际情况。
   
   
   

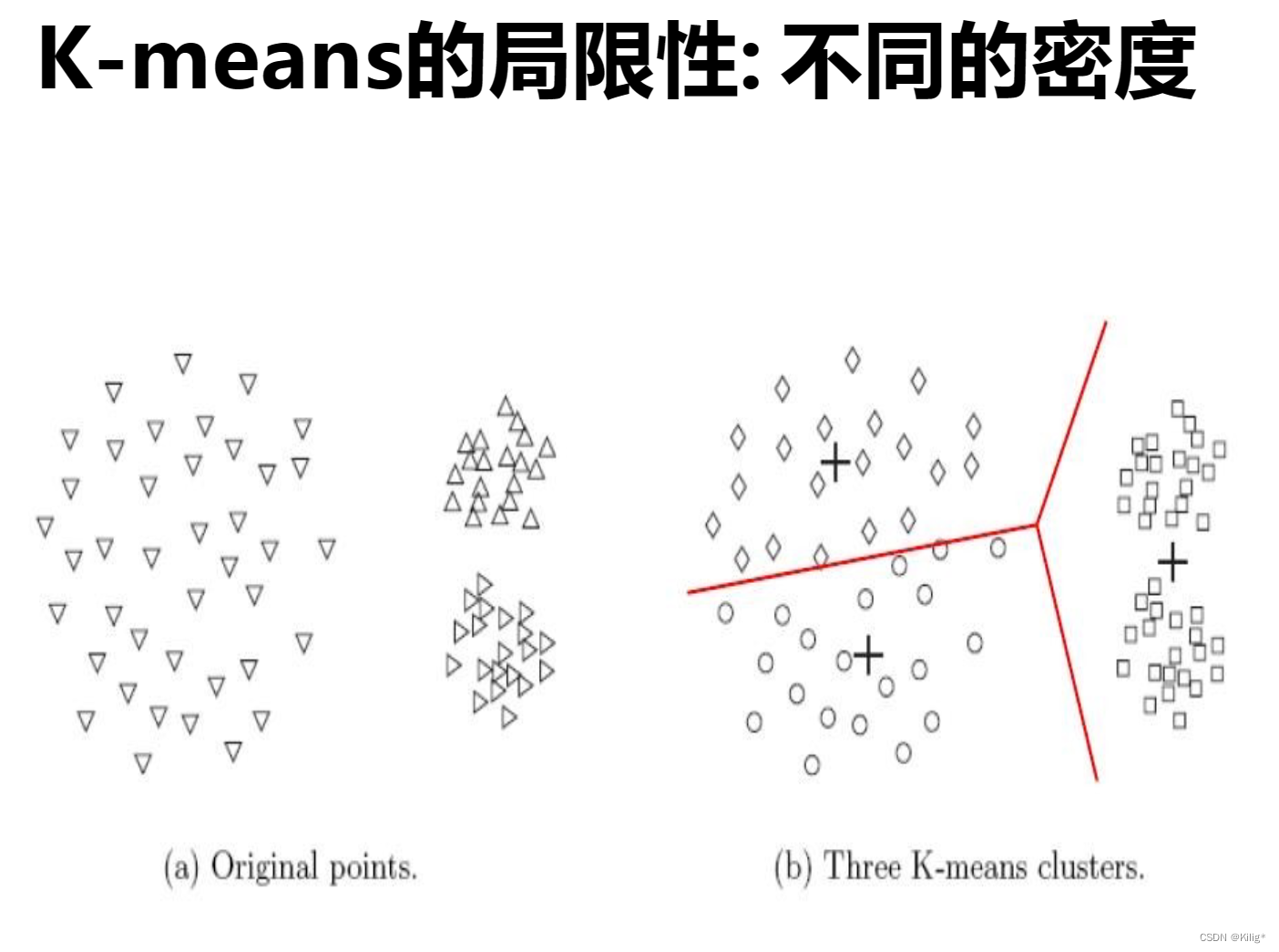
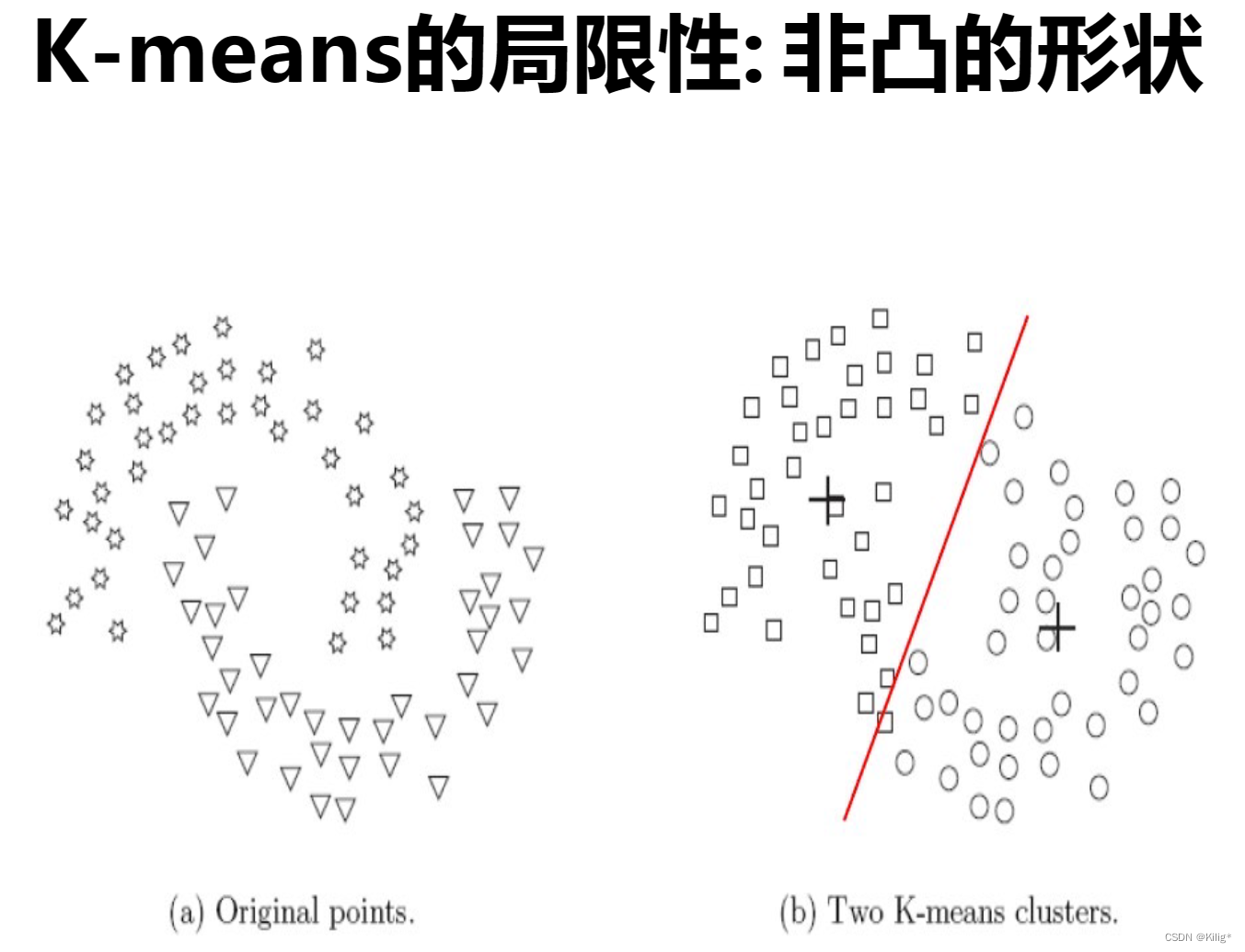
解决方案：

针对K-means的局限性，可以采用以下解决方案：

1. 软聚类方法：使用软聚类方法，如高斯混合模型（Gaussian Mixture Models，GMM），允许数据点以一定的概率属于不同的簇，而不是强制性地将其分配到唯一的簇。
2. 采用不同形状的簇：对非球形簇结构，可以考虑使用其他形式的聚类算法，如密度聚类（DBSCAN）等，这些算法对数据的形状和密度分布没有特定的假设。

高斯混合模型（Gaussian Mixture Models，GMM）

多维高斯分布的概率密度函数：

对于一个 $D$ 维的随机向量 $\mathbf{x}=(x_1,x_2,\dots ,x_D{)}^T$，其多维高斯分布的概率密度函数可以表示为：

$$\mathcal{N}(\mathbf{x}|\mathbf{\mu },\mathbf{\Sigma })=\frac{1}{(2\pi {)}^{D/2}|\mathbf{\Sigma }{|}^{1/2}}\exp \left(?\frac{1}{2}(\mathbf{x}?\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{?1}(\mathbf{x}?\mathbf{\mu })\right)$$

其中，

• $\mathbf{\mu }=({\mu }_1,{\mu }_2,\dots ,{\mu }_D{)}^T$ 是均值向量，表示随机向量每个维度的均值。
• $\mathbf{\Sigma }$ 是协方差矩阵，表示随机向量各维度之间的协方差。
• $|\mathbf{\Sigma }|$ 是协方差矩阵的行列式。
• ${}^T$ 表示向量的转置。
• $\exp (?)$ 是自然指数函数。

高斯混合模型（Gaussian Mixture Model，GMM）

模型形式：

假设有 $N$ 个数据点 ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_N$，GMM 的概率密度函数可表示为：

$$p(\mathbf{x})=\sum _{k=1}^K{\pi }_k\mathcal{N}(\mathbf{x}|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$$

其中，

• $K$ 是高斯分布的数量（聚类数目）；
• ${\pi }_k$ 是第 $k$ 个高斯分布的权重，满足 ${\sum }_{k=1}^K{\pi }_k=1$；
• $\mathcal{N}(\mathbf{x}|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)$ 是多维高斯分布密度函数，${\mathbf{\mu }}_k$ 是第 $k$ 个高斯分布的均值向量，${\mathbf{\Sigma }}_k$ 是其协方差矩阵。

EM算法迭代过程：

1. 初始化：随机初始化模型参数（各高斯分布的均值、协方差矩阵和权重）。
2. E步骤（Expectation）：
   • 计算每个数据点 ${\mathbf{x}}_n$ 属于每个高斯分布的后验概率，即第 $k$ 个高斯分布生成第 $n$ 个数据点的概率：
     $$\gamma (z_{nk})=\frac{{\pi }_k\mathcal{N}({\mathbf{x}}_n|{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k)}{{\sum }_{j=1}^K{\pi }_j\mathcal{N}({\mathbf{x}}_n|{\mathbf{\mu }}_j,{\mathbf{\Sigma }}_j)}$$
3. M步骤（Maximization）：
   • 重新估计参数：
     • 更新每个高斯分布的权重 ${\pi }_k$：
       $${\pi }_k=\frac{1}{N}\sum _{n=1}^N\gamma (z_{nk})$$
     • 更新每个高斯分布的均值 ${\mathbf{\mu }}_k$：
       $${\mathbf{\mu }}_k=\frac{{\sum }_{n=1}^N\gamma (z_{nk}){\mathbf{x}}_n}{{\sum }_{n=1}^N\gamma (z_{nk})}$$
     • 更新每个高斯分布的协方差矩阵 ${\mathbf{\Sigma }}_k$：
       $${\mathbf{\Sigma }}_k=\frac{{\sum }_{n=1}^N\gamma (z_{nk})({\mathbf{x}}_n?{\mathbf{\mu }}_k)({\mathbf{x}}_n?{\mathbf{\mu }}_k{)}^T}{{\sum }_{n=1}^N\gamma (z_{nk})}$$
4. 重复迭代：重复执行E步骤和M步骤，直到模型参数收敛或达到预设的迭代次数。

在EM算法中，E步骤计算数据点属于每个高斯分布的后验概率，M步骤根据这些后验概率重新估计模型参数，迭代更新直至收敛。这个过程旨在最大化观测数据的似然函数，使得模型能够更好地拟合数据。

K-means 与 高斯混合模型（GMM）的对比：

K-means：

• 硬聚类算法：每个数据点仅属于一个簇。
• 假设：假定簇为球形，并对数据进行硬划分。
• 速度快：简单且计算效率高，适用于大规模数据集。

高斯混合模型（GMM）：

• 软聚类算法：允许一个数据点以一定概率分配到不同的聚类中心。
• 假设：允许簇有不同形状和大小，并用高斯分布建模数据分布。
• 灵活性：适用于更广泛的数据形状和分布。
• 更复杂的模型：与K-means相比，GMM具有更复杂的模型和参数（均值、协方差、权重）。

高斯混合模型（GMM）的优缺点：

优点：

1. 灵活性：对数据分布的假设更加灵活，可以拟合各种形状和大小的簇。
2. 软聚类：允许数据以一定概率属于不同的聚类中心，更符合实际场景。
3. 能量表达能力强：GMM是一个强大的建模工具，能够捕获数据中的复杂关系。

缺点：

1. 计算复杂度高：相比于K-means，GMM具有更高的计算复杂度，特别是在高维数据上。
2. 对初始值敏感：GMM对于初始参数值敏感，不同的初始值可能会导致不同的聚类结果。
3. 可能陷入局部最优解：迭代优化过程可能陷入局部最优解，影响模型的效果。

选择应用场景：

• 如果数据集具有明显的簇结构、数据分布近似球形，并且对计算速度要求较高，K-means可能是一个不错的选择。
• 如果数据集具有复杂的形状、大小和分布，或者需要更丰富的数据建模，GMM可能更适合。
• 通常，可以根据数据的特点和任务的需求来选择适合的聚类算法。

层次聚类

簇之间的相似性度量

最小距离

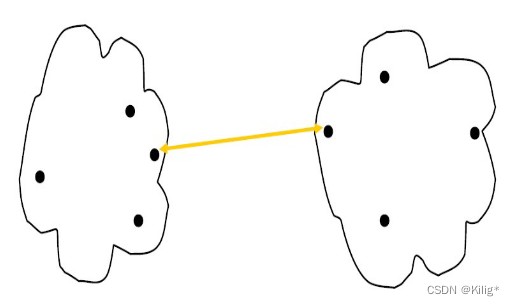
适合发现凸型簇或者非等向性的簇，对异常值不敏感。它衡量的是两个簇中最近的两个数据点的距离，所以在形成簇的过程中，容易受到离群点的影响。

最大距离

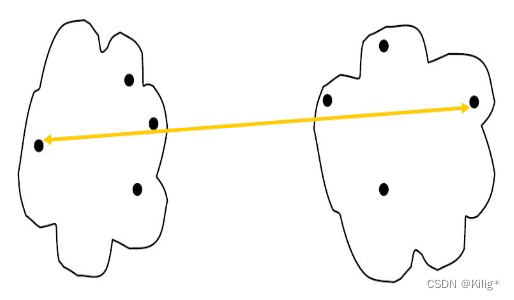
适合发现球状簇，能够很好地处理不同大小和密度的簇，对噪声和异常值比较稳健。它考虑的是两个簇中距离最远的两个数据点之间的距离，使得形成的簇间距离更大。

平均距离

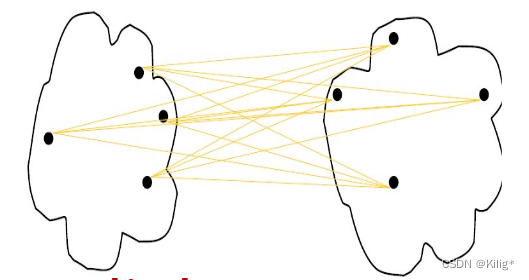
对各种类型的簇都相对适用，通常被视为对最小距离和最大距离的折衷方案。它计算两个簇中所有数据点之间的平均距离，能够平衡最小和最大距离法的影响。

中心点距离

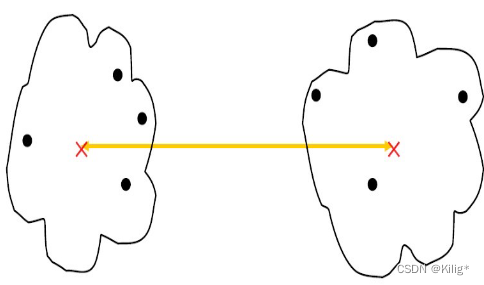
考虑簇之间的中心点（质心）之间的距离。这种方法对异常值相对较敏感，因为它完全依赖于簇的中心点，并且不适合非凸形状的簇。

层次聚类是一种按照层次结构组织的聚类方法，其主要思想是将数据点逐步合并或分割，形成一个层次化的聚类结构。层次聚类方法有两种主要的方法：凝聚聚类（Agglomerative Clustering）和分裂聚类（Divisive Clustering）。这里我将介绍凝聚聚类的过程。

凝聚聚类过程：

凝聚聚类是一种自底向上的聚类方法，其步骤如下：

1. 初始化：

   • 将每个数据点视为一个单独的簇。

2. 计算相似度或距离：

   • 计算所有数据点之间的相似度或距离（如欧氏距离、曼哈顿距离、相关系数等）。

3. 合并最近的簇：

   • 找到相似度或距离最小的两个簇，并将它们合并成一个新的簇。
   • 合并簇的方式可以根据不同的距离度量方法来确定，比如单链接（single-linkage）、全链接（complete-linkage）、平均链接（average-linkage）等。

4. 更新相似度矩阵：

   • 更新相似度矩阵，重新计算新簇与其他簇之间的距离或相似度。

5. 重复合并步骤：

   • 重复进行合并步骤，不断合并距离最近的簇，直到满足某个停止条件（比如指定簇的数量、距离阈值等）。

6. 构建聚类树（Dendrogram）：

   • 沿着合并过程，可以记录每次合并的簇以及它们的距离，构建层次聚类树或者称为树状图（Dendrogram）。

7. 树状图的剪枝（可选）：

   • 可以根据业务需求或者树状图的结构，通过剪枝来选择最终的聚类结果，确定簇的数量。

凝聚聚类方法将每个数据点作为一个簇，然后通过不断合并最接近的簇，逐步形成层次化的聚类结构。最终，通过聚类树（Dendrogram）或剪枝得到最终的聚类结果。

DBSCAN

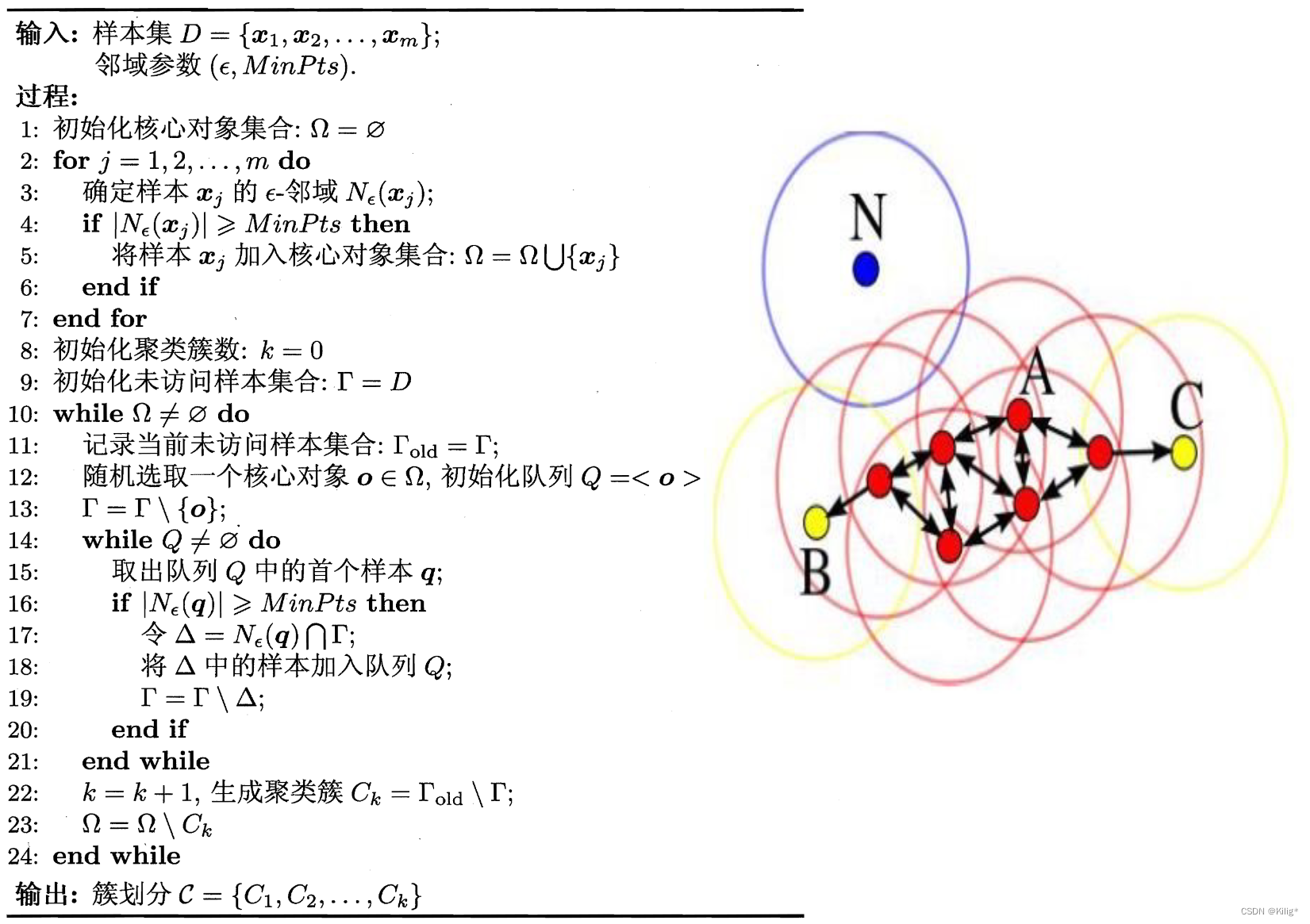
DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，能够识别具有不同密度的样本点，并能够有效地处理噪声点。DBSCAN通过定义“邻域”和“核心点”来识别簇，并能够发现任意形状的簇结构。

DBSCAN算法步骤：

1. 定义邻域：

   • 以一个指定的距离阈值 $\epsilon$ 作为半径，对每个数据点 $\mathbf{p}$ 进行邻域定义。
   • 如果在以 $\mathbf{p}$ 为中心，半径为 $\epsilon$ 的圆球内包含超过指定数量（MinPts）的点，则 $\mathbf{p}$ 被视为核心点。

2. 寻找核心点和连接簇：

   • 根据第一步的定义，寻找所有核心点，并将每个核心点的邻域内的点归为同一个簇。
   • 如果点 $\mathbf{q}$ 在 $\mathbf{p}$ 的邻域内，且 $\mathbf{q}$ 也是核心点，则将 $\mathbf{q}$ 的簇合并到 $\mathbf{p}$ 所在的簇中。

3. 处理噪声点：

   • 将不能成为核心点，也不在任何核心点的邻域内的数据点视为噪声点或边界点。

DBSCAN的特点：

• 能处理任意形状的簇：相比于K-means等硬聚类算法，DBSCAN能够发现任意形状的簇，对簇的形状没有特定的假设。
• 对噪声点鲁棒：DBSCAN能够识别和过滤噪声点，将其视为离群点。
• 不需要提前指定簇的数量：与K-means等需要提前指定簇数量的算法不同，DBSCAN不需要这个先验信息。

参数说明：

• $\epsilon$：邻域的半径大小。
• MinPts：定义核心点时所需的最小邻域点数。

优势与局限性：

优势：

• 能够识别任意形状的簇结构。
• 对噪声和离群点有较好的鲁棒性。
• 不需要提前指定簇的数量。

局限性：

• 对于密度不均匀的数据或具有差异密度的簇效果可能不理想。
• 对于高维数据集，由于“维度灾难”问题，需要谨慎选择距离阈值和邻域点数。

例题

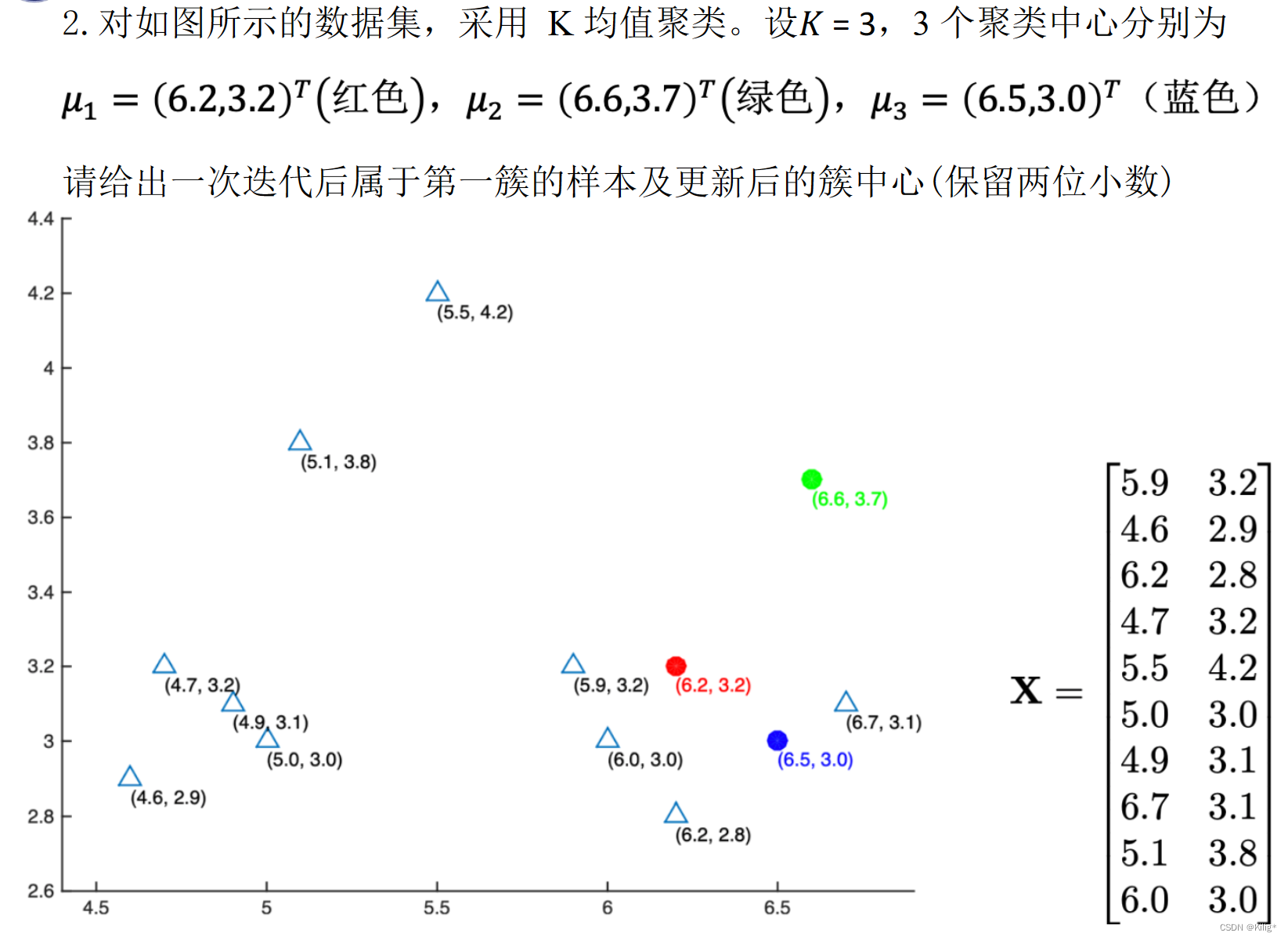
import math
import numpy as np
data=[[5.9,  3.2],
[4.6,  2.9],
[6.2,  2.8],
[4.7,  3.2],
[5.5,  4.2],
[5.0,  3.0],
[4.9,  3.1],
[6.7,  3.1], 
[5.1,  3.8], 
[6.0,  3.0]]

center = [[6.2,3.2],[6.6,3.7],[6.5,3.0]]
def cal_distance(point1, point2):
    # 计算两点之间的欧氏距离
    distance = math.sqrt((point1[0] - point2[0])**2 + (point1[1] - point2[1])**2)
    return distance
def get_min_index(lst):
    # 获取最小值
    min_value = min(lst)
    # 获取最小值的下标
    min_index = lst.index(min_value)
    return min_index

data_dict = {0:[],1:[],2:[]}

for i in data:
    tmp = []
    print("点:",i,end = '\t')
    for j in center:
        tmp.append(round(cal_distance(i,j),2))
        print(f"距离类别{center.index(j)}的距离:",round(cal_distance(i,j),2),end = '\t')
    data_dict[get_min_index(tmp)].append(i)
    print("分配给类别:",get_min_index(tmp))
    
for i in data_dict.keys():
    print(f"类别{i}的中心为:{np.array(data_dict[i]).mean(axis = 0)}")

输出:

点: [5.9, 3.2]	距离类别0的距离: 0.3	距离类别1的距离: 0.86	距离类别2的距离: 0.63	分配给类别: 0
点: [4.6, 2.9]	距离类别0的距离: 1.63	距离类别1的距离: 2.15	距离类别2的距离: 1.9	分配给类别: 0
点: [6.2, 2.8]	距离类别0的距离: 0.4	距离类别1的距离: 0.98	距离类别2的距离: 0.36	分配给类别: 2
点: [4.7, 3.2]	距离类别0的距离: 1.5	距离类别1的距离: 1.96	距离类别2的距离: 1.81	分配给类别: 0
点: [5.5, 4.2]	距离类别0的距离: 1.22	距离类别1的距离: 1.21	距离类别2的距离: 1.56	分配给类别: 1
点: [5.0, 3.0]	距离类别0的距离: 1.22	距离类别1的距离: 1.75	距离类别2的距离: 1.5	分配给类别: 0
点: [4.9, 3.1]	距离类别0的距离: 1.3	距离类别1的距离: 1.8	距离类别2的距离: 1.6	分配给类别: 0
点: [6.7, 3.1]	距离类别0的距离: 0.51	距离类别1的距离: 0.61	距离类别2的距离: 0.22	分配给类别: 2
点: [5.1, 3.8]	距离类别0的距离: 1.25	距离类别1的距离: 1.5	距离类别2的距离: 1.61	分配给类别: 0
点: [6.0, 3.0]	距离类别0的距离: 0.28	距离类别1的距离: 0.92	距离类别2的距离: 0.5	分配给类别: 0
类别0的中心为:[5.17142857 3.17142857]
类别1的中心为:[5.5 4.2]
类别2的中心为:[6.45 2.95]